小升初数学真题汇编6(全国通用版含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初数学真题汇编6(全国通用版)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.(2022·河北保定·统考小升初真题)几个人握手,每两人之间都握手一次,其中小明一共握了5次,大家一共握了( )次。
A.25 B.20 C.15
2.(2022·湖南娄底·统考小升初真题)下列和成正比例关系的是( )。
A. B. C.(>0) D.
3.(2022·湖南岳阳·统考小升初真题)从A地到B地,甲车要行小时,乙车要行1小时,甲车与乙车的速度比是( )。
A.∶1 B.1∶ C.4∶5 D.5∶4
4.(2022·黑龙江哈尔滨·统考小升初真题)下面的说法不正确的是( )。
A.2∶3和0.6∶0.9能组成比例。
B.圆柱的侧面积一定,底面周长和高成正比例。
C.如果甲在乙的东偏南30°方向,则乙在甲的西偏北30°方向。
5.(2022·云南昆明·统考小升初真题)0.5这个数,在下面生活场景中使用最合适的是( )。
A.两本数学书的质量 B.一个书包的价钱
C.一本数学书封面的大小 D.昆明到大理的路程
6.(2022·安徽合肥·统考小升初真题)用、、三张数字卡片,一共可以组成( )个不同的三位数。
A.4 B.6 C.8
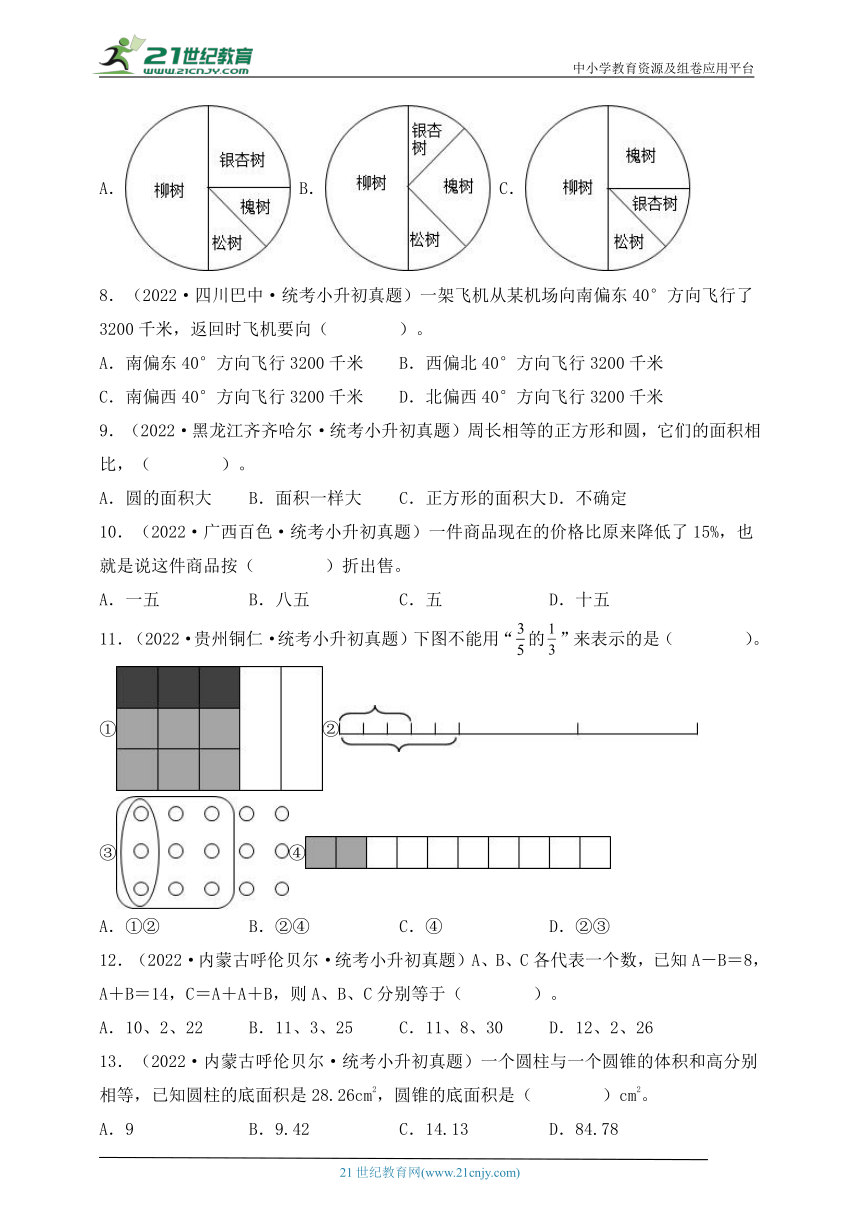
7.(2022·安徽合肥·统考小升初真题)某小区中心花园四种树木棵数统计如表。能正确表示表中信息的扇形统计图是( )。
树木类别 柳树 槐树 松树 银杏树
棵数 120 60 30 30
A. B. C.
8.(2022·四川巴中·统考小升初真题)一架飞机从某机场向南偏东40°方向飞行了3200千米,返回时飞机要向( )。
A.南偏东40°方向飞行3200千米 B.西偏北40°方向飞行3200千米
C.南偏西40°方向飞行3200千米 D.北偏西40°方向飞行3200千米
9.(2022·黑龙江齐齐哈尔·统考小升初真题)周长相等的正方形和圆,它们的面积相比,( )。
A.圆的面积大 B.面积一样大 C.正方形的面积大 D.不确定
10.(2022·广西百色·统考小升初真题)一件商品现在的价格比原来降低了15%,也就是说这件商品按( )折出售。
A.一五 B.八五 C.五 D.十五
11.(2022·贵州铜仁·统考小升初真题)下图不能用“的”来表示的是( )。
①②
③④
A.①② B.②④ C.④ D.②③
12.(2022·内蒙古呼伦贝尔·统考小升初真题)A、B、C各代表一个数,已知A-B=8,A+B=14,C=A+A+B,则A、B、C分别等于( )。
A.10、2、22 B.11、3、25 C.11、8、30 D.12、2、26
13.(2022·内蒙古呼伦贝尔·统考小升初真题)一个圆柱与一个圆锥的体积和高分别相等,已知圆柱的底面积是28.26cm2,圆锥的底面积是( )cm2。
A.9 B.9.42 C.14.13 D.84.78
14.(2022·广东梅州·统考小升初真题)下列说法正确的是( )。
A.一批水果重160%吨 B.一条射线长2.2m C.1的倒数是1
15.(2022·云南曲靖·统考小升初真题)当b=( )时,(36-4b)÷8=0。
A.9 B.7 C.8 D.6
16.(2022·湖南怀化·统考小升初真题)一项工程,6天完成工程的,照这样计算,完成余下的工程还需要( )天。
A.24 B.20 C.5
17.(2022·湖南怀化·统考小升初真题)三个连续偶数,第一个是a,最后一个是( )。
A.a+2 B.a+3 C.a+4
18.(2022·辽宁沈阳·统考小升初真题)将如图中的纸环,沿虚线剪开,可以得到( )个纸环。
A.1 B.2 C.3
19.(2022·辽宁沈阳·统考小升初真题)在“用长方形纸卷圆柱”的实践活动中,我们发现用面积相等的长方形卷成不同的圆柱,( )。
A.侧面积相等,体积也相等
B.底面半径越小,体积越小
C.底面半径越小,体积越大
20.(2022·陕西安康·统考小升初真题)把一个棱长2分米的正方体削成一个最大的圆柱,这个圆柱的侧面积是( )。
A.18.84平方分米 B.6.28平方分米 C.3.14平方分米 D.12.56平方分米
21.(2022·河北唐山·统考小升初真题)用三根以下长度的小棒不能围成三角形的是( )。
A.2cm、3cm、4cm B.2cm、2cm、3cm C.2cm、2cm、2cm D.2cm、2cm、4cm
22.(2022·河北唐山·统考小升初真题)小军想用计算器验算567×39的结果是否正确,但计算器的按键9坏掉了。以下几种方法不能正确验算的是( )。
A.567×3×13 B.567×40-40 C.567×40-567 D.567×38+567
23.(2022·江西赣州·统考小升初真题)一个圆柱和一个圆锥等底等高,圆柱的体积比圆锥多6.4立方分米,圆柱的体积是( )立方分米。
A.1.6 B.3.2 C.6.4 D.9.6
24.(2022·吉林白山·统考小升初真题)如果m和n都是非0自然数,m÷n=23,那么m和n的最小公倍数是( )。
A.m B.n C.23 D.无法确定
25.(2022·河南驻马店·校考小升初真题)如图,转盘中有8个数字,现在淘气将飞镖投向转盘,投中( )情况的可能性最大。
A.2的倍数 B.不是3的倍数 C.大于5的数 D.不大于5的数
26.(2022·山东临沂·统考小升初真题)用一块长是8厘米,宽是6厘米的长方形厚纸板,剪出一个最大的正方形,剩下图形的面积是( )平方厘米。
A.12 B.36 C.48
27.(2022·甘肃庆阳·统考小升初真题)花店在银行的北偏西30°方向200m处,那么银行就在花店的( )方向200m处。
A.东偏南30° B.南偏东30° C.西偏北30° D.北偏西30°
28.(2022·甘肃庆阳·统考小升初真题)要反映牛奶中水、蛋白质、脂肪等含量,用( )更合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表
29.(2022·辽宁大连·统考小升初真题)下面四个图形都是由6个同样大的小正方形组成的,不能折叠成正方体的是( )。
A. B. C. D.
30.(2022·甘肃平凉·统考小升初真题)2022年平凉市的银行年利率为4.6%,李华的妈妈在2022年初存了30000元为了给她的儿子在2025年高考结束后旅游使用,则在2025年共取( )元。
A.1980 B.34600 C.31380 D.34140
31.(2022·湖南邵阳·统考小升初真题)把25克盐溶入200克水中制成盐水,盐和盐水质量的比是( )。
A.1∶8 B.1∶9 C.1∶10 D.1∶11
32.(2022·湖南邵阳·统考小升初真题)在下面的图形中,有4条对称轴的是( )。
A.三角形 B.长方形 C.正方形 D.圆形
33.(2022·广东深圳·统考小升初真题)已知三角形一个角是30°,另外两个内角的度数比是1∶4,那么这个三角形是( )。
A.锐角三角形 B.直角三角形
C.等腰直角三角形 D.钝角三角形
34.(2022·广东深圳·统考小升初真题)13.6%去掉百分号后,这个数就( )。
A.扩大为原来的100倍 B.缩小为原来的
C.大小不变 D.无法确定
35.(2022·广东深圳·统考小升初真题)大于0而小于1的数( )。
A.一个也没有 B.无数个 C.有10个 D.以上都不是
36.(2022·广东深圳·统考小升初真题)如图,已知OA=AB=BC=1cm,那么点P在点O的( )处。
A.北偏西30°,20km B.北偏西60°,20km
C.北偏西30°,40km D.北偏西60°,40km
37.(2022·山东枣庄·统考小升初真题)科学家将新冠病毒疫苗检测器按照10∶1的比例尺画在图上,它在图纸上的长度为4厘米,它的实际长度是( )毫米。
A.400 B.40 C.4 D.0.4
38.(2022·山东枣庄·统考小升初真题)用小棒搭房子,搭一间用5根,搭三间用13根,如图,照这样子搭504间房子要用( )根小棒。
A.2015 B.2016 C.2017 D.2018
39.(2022·河南鹤壁·统考小升初真题)体育课上,老师喊的口令是“向后转”,你的身体应该( )。
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转180° D.逆时针旋转180°
40.(2022·陕西汉中·统考小升初真题)下面各数中,与最接近的是( )。
A.0.374 B.0.6 C.0.63 D.65%
41.(2022·四川广安·统考小升初真题)用9个相同的铁圆锥可以熔铸成( )个与其等底等高的圆柱。
A.3 B.6 C.12 D.27
42.(2022·黑龙江鸡西·统考小升初真题)一个角的两条边是两条( )。
A.直线 B.射线 C.线段 D.以上都对
43.(2022·黑龙江鸡西·统考小升初真题)下面属于方程的是( )。
A.x+5 B.5+6=11 C.x-10=3 D.x÷12>20
44.(2022·辽宁鞍山·统考小升初真题)如图,一个圆锥体酒杯,倒入一些红酒,红酒深为圆锥高的一半,满杯红酒的体积是现在杯中红酒体积的( )倍。
A.2 B.3 C.4 D.8
45.(2022·河北石家庄·统考小升初真题)有30个小球,其中有一个是次品比其它小球轻一些。用天平称重的方法至少( )次一定能找出次品。
A.3 B.4 C.5
46.(2022·江苏南京·统考小升初真题)小明所在班级学生平均身高是1.41米,小强所在班级学生平均身高是1.4米,小明和小强相比( )。
A.小明高 B.小强高 C.一样高 D.无法确定谁高
47.(2022·河南商丘·统考小升初真题)有一串彩色珠子,按2红3黄1黑的顺序排列,第48颗珠子是( )色。
A.红 B.黄 C.黑
48.(2022·河南商丘·统考小升初真题)如果=(x、y都不为0),那么x和y( ),如果9∶x=y∶2.3,那么x和y( )。
A.成正比例;成反比例 B.成反比例;成正比例 C.不成比例;成正比例
49.(2022·河北邯郸·统考小升初真题)一条绳子剪去米,还剩,那么剪去部分和剩下部分相比,( )。
A.剪去的长 B.一样长 C.剩下的长 D.无法确定
50.(2022·山西晋中·统考小升初真题)有一个平衡支架,(如图)在支架左右两边各挂一个质量相同的袋子,右边袋子里放( )kg的物体,支架才能保持平衡。
A.4 B.6 C.8
参考答案:
1.C
【分析】每两人握一次手,小明一共握了5次,即每人都要和其他5人握一次手,那么一共有6个人,共握手(5×6)次,握手是在两人之间进行的,要去掉重复计算的次数,最后结果除以2,据此解答。
【详解】5+1=6(人)
5×6÷2
=30÷2
=15(次)
所以,大家一共握了15次。
故答案为:C
【点睛】本题主要考查搭配问题,解题时也可以用枚举法解答,注意去掉重复计算的情况是解答题目的关键。
2.B
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例;如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.,和一定,与不成比例;
B.,则,比值一定,与成正比例关系;
C.,则,乘积一定,与成反比例关系;
D.,差一定,与不成比例。
故答案为:B
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
3.D
【分析】把甲、乙两地的路程看成“1”,根据“速度=路程÷时间”,分别写出甲、乙两车的速度,再根据比的意义,即可写出甲车与乙车的速度比,并化成最简整数比。
【详解】(1÷)∶(1÷1)
=∶1
=5∶4
故答案为:D
【点睛】此题是考查比的意义与化简。关键是根据路程、时间、速度三者之间的关系,分别求出甲、乙两车的速度。
4.B
【分析】(1)根据比例的意义:表示两个比相等的式子,分别化简每一组比,再看它们的比值是否相等即可;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,即可解答;
(3)根据位置的相对性可知,它们的方向相反,角度相等,据此解答。
【详解】A.2∶3=,0.6∶0.9=,比值相等,2∶3和0.6∶0.9能组成比例,原题说法正确;
B.圆柱的底面周长×高=侧面积(一定),乘积一定,所以它的底面周长和高成反比例,原题说法错误;
C.如果甲在乙的东偏南30°方向,则乙在甲的西偏北30°方向,原题的说法正确。
故答案为:B
【点睛】判断成正反比例是本题的一个难点,需要熟悉其中的数量关系,以及正反比例的辨识方法。
5.A
【分析】根据生活经验以及对质量单位、长度单位、人民币单位和数据大小的认识,结合实际情况进行选择即可,据此解答。
【详解】两本数学书的质量可以为0.5kg。
故答案为:A
【点睛】解决本题要注意联系生活实际、计量单位和数据的大小,灵活选择。
6.A
【分析】0不能在最高位,先排百位有2种选择,再排十位有2种选择,然后排个位有1种选择,然后根据乘法原理解答即可。
【详解】2×2×1=4(个)
故答案为:A
【点睛】本题考查了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×……×mn种不同的方法。
7.C
【分析】把四种树木棵数的总数看作单位“1”,根据求一个数是另一个数的百分之几,分别求出四种树所占的分率,然后与下面3幅统计图进行比较即可。
【详解】120+60+30+30=240(课)
柳树:120÷240×100%=50%
槐树:60÷240×100%=25%
松树:30÷240×100%=12.5%
银杏树:30÷240×100%=12.5%
据此可知;柳树要占一半,而松树和银杏数是相等的,只有C选项符合题意。
故答案为:C
【点睛】考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
8.D
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
【详解】一架飞机从某机场向南偏东40°方向飞行了3200千米,返回时飞机要向北偏西40°方向飞行3200千米。
故答案为:D
【点睛】本题主要考查了学生对位置相对性的掌握情况,画图可以帮助理解。
9.A
【分析】假设出它们的周长,根据它们的周长求出正方形的边长和圆的半径,最后利用“”“”求出正方形和圆的面积,并比较大小。
【详解】假设它们的周长为6.28。
正方形的面积:(6.28÷4)×(6.28÷4)
=1.57×1.57
=2.4649
圆的面积:3.14×(6.28÷3.14÷2)2
=3.14×(2÷2)2
=3.14×1
=3.14
因为3.14>2.4649,所以圆的面积大。
故答案为:A
【点睛】掌握正方形和圆的周长和面积的计算公式是解答题目的关键。
10.B
【分析】把原价看成单位“1”,比原来降低了15%,也就是按(1﹣15%)出售的,根据折扣与百分数的关系:几折就表示百分之几十,据此解答。
【详解】1-15%=85%
85%也就是八五折,所以这件商品按八五折出售。
故答案为:B
【点睛】解答本题的关键是理解百分数与折扣的关系。
11.B
【分析】①把长方形平均分成5份,涂其中的3份,表示;然后再把,平均分成3份,涂其中的1份,表示为的,用分数表示为×;
②把整条线段看作单位“1”,平均分成3份,取其中的1份,表示,然后再把平均分成5份,取其中的3份,表示为“的”,用分数表示为×;
③把所有图形看作单位“1”,平均分成5份,涂其中的3份,表示;然后再把,平均分成3份,涂其中的1份,表示为的,用分数表示为;
④把整个长方形看作单位“1”,平均分成10份,涂其中的2份,表示;约分后是,但并不能用表示。
【详解】根据分析得,不能用“的”来表示的是②④。
故答案为:B
【点睛】本题主要考查分数乘法的意义及作图,关键是分清平均分成的份数及取的份数。
12.B
【分析】根据A-B=8,可得A=B+8,将其代入A+B=14中,可得到B的值,进而求出A和C的值。
【详解】根据分析得,把A=B+8代入A+B=14中
可得:B+8+B=14
2B=14-8
2B=6
B=3
A=8+3=11;
C=11+11+3=25。
故答案为:B
【点睛】此题主要考查了简单的等量代换问题,要熟练掌握。再运用等式的性质求出A、B、C的值。
13.D
【分析】圆柱体体积公式V=sh,圆锥体体积公式V=sh,当圆柱体和圆锥体的体积和高都相等时,圆锥体的底面积是圆柱体底面积的3倍。
【详解】28.26×3=84.78(cm2)
故答案为:D
【点睛】解答此题主要根据等底等高的圆锥体的体积是圆柱体体积的,当圆柱体与圆锥体等高等体积时,圆锥体的底面积是圆柱体底面积的3倍。
14.C
【分析】百分数是表示一个数占另一个数的百分比,不能加单位;射线向一端无限延长,不能测量长度;1的倒数是1,据此选择。
【详解】A.百分数后面不能加单位,原题说法错误;
B.射线不能测量长度,原题说法错误;
C.1的倒数是1,原题说法正确。
故答案为:C
【点睛】本题考查了百分数的意义、倒数的意义及射线的特征。
15.A
【分析】根据题意,可列出方程(36-4b)÷8=0,解方程即可得出结论。
【详解】(36-4b)÷8=0
解:(36-4b)÷8×8=0×8
36-4b=0
36-4b+4b=0+4b
4b=36
4b÷4=36÷4
b=9
故答案为:A
【点睛】本题考查的是解方程,要利用等式的性质。
16.A
【分析】把这项工程的工作总量看作单位“1”,用6天除以,可以计算出完成这项工程共需要多少天,再用完成这项工程共需要的天数减去6,可以计算出完成余下的工程还需要多少天。
【详解】
=30-6
=24(天)
故答案为:A
【点睛】本题解题关键是把这项工程的工作总量看作单位“1”,根据分数除法的意义,先计算出完成这项工程共需要多少天,再用减法计算出完成余下的工程还需要多少天。
17.C
【分析】根据2的倍数叫做偶数,又叫做双数即可解答。
【详解】三个连续偶数,第一个是a,最后一个是a+4。
故答案为:C
【点睛】本题考查偶数的概念,2的倍数叫偶数,相邻偶数的差是2。
18.A
【分析】莫比乌斯带:拿一张白的长纸条,把一面涂成黑色,然后把其中一端翻一个身,粘成一个莫比乌斯带,用剪刀沿纸带的中央把它剪开。纸带不仅没有一分为二,反而剪出一个两倍长的纸环;由此求解。
【详解】将图中的纸环,沿虚线剪开,可以得到一个两倍长的纸环。
故答案为:A
【点睛】熟知莫比乌斯带的特点是解决本题的关键。
19.B
【分析】根据圆柱的体积公式:V=πr2h,在“用长方形纸卷圆柱”的实践活动中,我们发现用面积相等的长方形卷成不同的圆柱,底面半径越小,体积就越小。据此解答即可。
【详解】根据分析可知,在“用长方形纸卷圆柱”的实践活动中,我们发现用面积相等的长方形卷成不同的圆柱,底面半径越小,体积就越小。
故答案为:B
【点睛】本题考查的目的是理解掌握圆柱体积的意义及应用。
20.D
【分析】根据题意,棱长是2分米的正方体木块,削成一个最大的圆柱,则它的直径为2分米,高也为2分米,根据圆柱的侧面积公式S=Ch,计算即可解答。
【详解】3.14×2×2
=6.28×2
=12.56(平方分米)
故答案为:D
【点睛】根据题意,把正方体削成一个最大的圆柱,则它的直径为原来的正方体的棱长,高也为正方体的棱长,再根据圆柱的侧面积公式计算即可。
21.D
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【详解】A.2cm+3cm>4cm,能围成三角形;
B.2cm+2cm>3cm,能围成三角形;
C.2cm+2cm>2cm,能围成三角形;
D.2cm+2cm=4cm,不能围成三角形。
故答案为:D
【点睛】本题考查了三角形的三边关系的应用。
22.B
【分析】用计算器验算“567×39”,可是计算器中“9”的按键坏了,那么可以把39分解成两个数的和或差,用乘法分配律进行转换,或者把39分解成两个数的积,再运用乘法结合律把算式转换,从而解决问题。
【详解】A.根据乘法结合律可得:
567×39
=567×3×13
本选项能算出正确答案;
B.567×40-40
=40×(567-1)
=40×566
本选项不能算出正确答案;
C.根据乘法分配律可得:
567×39
=567×(40-1)
=567×40-567
本选项能算出正确答案;
D.根据乘法分配律可得:
567×39
=567×(38+1)
=567×38+567
本选项能算出正确答案。
故答案为:B
【点睛】解决本题关键是熟练掌握乘法结合律和乘法分配律。
23.D
【分析】等底等高的圆柱的体积是圆锥体积的3倍,则圆柱的体积看作3份,圆锥的体积看作1份,相差2份,正好是6.4立方分米,据此求出一份是多少,再乘圆柱对应的份数即可。
【详解】6.4÷2×3
=3.2×3
=9.6(立方分米)
故答案为:D
【点睛】熟练掌握等底等高的圆柱的体积和圆锥体积的倍数关系,是解答此题的关键。
24.A
【分析】由m和n都是非0自然数,m÷n=23,可知m和n是倍数关系,根据倍数关系的最小公倍数是较大数,据此解答。
【详解】m÷n=23,可知m和n是倍数关系,所以m和n的最小公倍数是m。
故答案为:A
【点睛】本题主要考查求两个数的最小公倍数的方法,注意倍数关系的最小公倍数是较大数。
25.B
【分析】可逐项列举出每种情况的数字各有多少个,根据个数的具体情况做选择。
【详解】A.2的倍数:2、4、6、8,共有4个;
B.不是3的倍数:1、2、4、5、7、8,共有6个;
C.大于5的数:6、7、8,共有3个;
D.不大于5的数:1、2、3、4、5,共有5个;
6>5>4>3,即投中不是3的倍数这种情况的可能性最大。
故答案为:B
【点睛】在等可能发生的事件中,如果出现该事件的情况较多,我们就说该事件发生的可能性较大。
26.A
【分析】根据题意可知,在这块长方形的纸板,剪出一个最大的正方形,这个正方形的边长等于长方形的宽,剩下图形的长是6厘米,宽是(8-6)厘米,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】6×(8-6)
=6×2
=12(平方厘米)
故答案为:A
【点睛】此题主要考查长方形的分割,关键是熟记公式有关长方形、正方形的面积公式。
27.B
【分析】根据位置的相对性可知:位置相对的两个物体所在的方向相反、角度相同、距离不变;据此解答。
【详解】花店在银行的北偏西30°方向200m处,那么银行就在花店的南偏东30°方向200m处。
故答案为:B
【点睛】本题主要考查位置的相对性,解题时要明确:位置相对的两个物体所在的方向相反、角度相同、距离不变。
28.C
【分析】条形统计图和统计表能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】要反映牛奶中水、蛋白质、脂肪等含量,用扇形统计图更合适。
故答案为:C
【点睛】此题应根据条形统计图、折线统计图、扇形统计图、统计表各自的特点进行解答。
29.A
【分析】根据正方体展开图的11种特征,即可确定哪个图形属于正方体展开图,能折叠成正方体,哪个图形不属于正方体展开图,不能折叠成正方体。
【详解】所给四个图形都是由6个同样大的小正方形组成的,不能折叠成正方体的是。
故答案为:A
【点睛】正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
30.D
【分析】根据本息和=本金+本金×利率×存期,代入数据解答即可。
【详解】30000+30000×4.6%×(2025-2022)
=30000+4140
=34140(元)
故答案为:D
【点睛】本题考查了存款利息相关问题,公式:本息和=本金+本金×利率×存期。
31.B
【分析】把25克盐溶入200克水中制成盐水,则盐水的质量是(25+200)克,根据比的意义,即可写出盐和盐水的质量比,并化成最简整数比。
【详解】25∶(25+200)
=25∶225
=1∶9
故答案为:B
【点睛】此题是考查比的意义及化简,两数相除又叫两个数的比,化简比根据比的基本性质。
32.C
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】A.等腰三角形有1条对称轴,等边三角形有3条对称轴,一般三角形没有对称轴;
B.长方形有2条对称轴;
C.正方形有4条对称轴;
D.圆有无数条对称轴。
故答案为:C
【点睛】此题考查了轴对称的意义及在实际图形当中的运用。
33.D
【分析】先根据三角形的内角和求出剩下的两个角的度数和,再按照比例分配求出另外两个角,即可解答。
【详解】180°-30°=150°
150°×
=150°×
=30°
150°×
=150°×
=120°
90°<120°<180°
这个三角形是钝角三角形。
故答案为:D
【点睛】利用三角形内角和180°,三角形的分类以及按比例分配问题的知识进行解答。
34.A
【分析】13.6%化成小数是0.136,它的小数点向右移动2位是13.6,就是扩大100倍,据此解答。
【详解】13.6%去掉百分号后,这个数就扩大到原来的100倍。
故答案为:A
【点睛】一个数(不等于0)后面添上百分号,这个数就缩小到原来的;一个百分数去掉百分号,这个数就扩大到原来的100倍。
35.B
【分析】大于0而小于1的一位小数有0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9;
大于0小于1的两位小数有:0.11、0.12、0.13、0.14、0.15、0.16、0.17、0.18、0.19、…0.91、0.92、0.93、0.94、0.95、0.96、0.97、0.98、0.99;
大于0小于1的三位小数有:0.101、0.102、…0.997、0.998、0.999;
以此类推,还有符合条件的四位小数、五位小数……。
【详解】根据分析可知:大于0而小于1的数有无数个。
故答案为:B
【点睛】此题考查的目的是理解小数的意义,掌握小数大小比较的方法。
36.D
【分析】圆上的点到圆心的距离处处相等,90°的角被平分成3个相等的角,则每个角为30°。
用方向和距离结合来描述路线时,要注意三个要素:一是观测点(即参照物),二是方向,三是距离。
【详解】OP=OB=20×2=40(千米)
90°÷3×2
=30°×2
=60°
点P在点O的北偏西60°,40km处。
故答案为:D
【点睛】本题考查圆的特征,图上距离和实际距离的换算,根据方向、角度和距离确定物体的位置。
37.C
【分析】图上距离和比例尺已知,利用“实际距离=图上距离÷比例尺”即可求得它的实际距离。
【详解】4÷10=0.4(厘米)
0.4(厘米)=4(毫米)
它的实际长度是4毫米。
故答案为:C
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
38.C
【分析】搭1间房子用5根小棒,即4×1+1;
搭2间房子用9根小棒,即4×2+1;
搭3间房子用13根小棒,即4×3+1;
……
搭504间房子用的小棒数为:4×504+1。
【详解】4×504+1
=2016+1
=2017(根)
故答案为:C
【点睛】本题主要考查数与形结合的规律,找出规律是解题的关键。
39.C
【分析】旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心,由此并结合实际可知:向左或向右转都是旋转了90°,向后转是旋转了180°;向左是逆时针,向右是顺时针,据此解答即可。
【详解】体育课上,老师喊的口令是“向后转”,你的身体应该顺时针旋转180°。
故答案为:C。
【点睛】解答此题的关键是明白:向左或向右转都是旋转了90°,向后转是旋转了180°。
40.C
【分析】将化为小数,再求出与各选项中的数相差多少,找出相差最小的选项。
【详解】=0.625
0.625-0.374=0.251
0.625-0.6=0.025
0.63-0.625=0.005
65%-0.625=0.025
0.005<0.025<0.251
可见各选项的数中,与最接近的是0.63。
故选:C
【点睛】解答此题需要掌握分数、百分数化小数的方法以及比较小数大小的方法。
41.A
【分析】根据圆柱和圆锥的体积公式可知,等底等高的圆柱的体积是圆锥体积的3倍,据此解答即可。
【详解】9÷3=3(个)
用9个相同的铁圆锥可以熔铸成3个与其等底等高的圆柱。
故答案为:A
【点睛】熟练掌握等底等高的圆柱的体积和圆锥体积的倍数关系,是解答此题的关键。
42.B
【详解】从一个顶点引出的两条射线所组成的图形叫做角,所以一个角的两条边是两条射线。
故答案为:B
43.C
【分析】含有未知数的等式叫做方程;由方程的意义可知,方程必须同时满足以下两个条件:(1)是等式;(2)含有未知数;两个条件缺一不可,据此逐项分析后再选择。
【详解】A.x+5,虽然含有未知数,但它不是等式,所以不是方程;
B.5+6=11,虽然是等式,但它没含有未知数,所以不是方程;
C.x-10=3,既含有未知数,又是等式,符合方程需要满足的两个条件,所以是方程;
D.x÷12>20,虽然含有未知数,但它不是等式,所以不是方程。
故答案为:C
【点睛】此题主要根据方程需要满足的条件来辨识方程,明确只有含有未知数的等式才是方程。
44.D
【分析】根据圆锥的体积公式:V=πr2h,设大圆锥的底面半径为r,高为h,则小圆锥的底面半径为r,高为h,把数据代入公式求出大小圆锥的体积,再根据求一个数是另一个数的几倍,用除法解答。
【详解】解:设大圆锥的底面半径为r,高为h,则小圆锥的底面半径为r,高为h;
πr2h÷[π×(r)2×h]
=πr2h÷[π×r2×h]
=πr2h÷[π×r2h]
=8
故答案为:D
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
45.B
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两边称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】第一次,把30个小球平均分成3份:10,10,10,任取两份分别放在天平两侧,若天平平衡,较轻的那个小球在未取的一份中,若天平不平衡,取较轻的一份继续;
第二次,取较轻的一份10个小球分成三份,3,3,4,取3个小球的两份分别放在天平两侧,若天平平衡,较轻的那个小球在未取的一份中,若天平不平衡,取较轻的一份继续;
第三次,取较轻的一份(3或4),取2个小球分别放在天平两侧,若天平平衡,较轻的那个是未取的那个小球或在未取的一份中,若天平不平衡,较轻一端是要找的那个小球;
第四次,取较轻的一份2个分别放在天平两侧,较轻一端是略轻的那个小球;
所以用天平称重的方法至少4次一定能找出次品。
故答案为:B
【点睛】解答此题的关键是将所给物品进行合理的分组,逐次称量,即可找出次品。
46.D
【分析】要判断小明和小强的高矮,根据“平均数=总身高÷全班总人数”,平均身高和总身高、总人数有关,并不能代表一个人的身高,由此可得,两个人的身高都不确定,故不能进行比较。
【详解】小明所在班级学生平均身高是1.41米,并不能代表小明的具体身高是1.41米;
小强所在班级学生平均身高是1.4米,并不能代表小强的平均身高是1.4米;
所以小明和小强相比,无法确定谁高。
故答案为:D
【点睛】此题主要考查对平均数的基础知识的掌握情况,做题时一定要弄清题意,认真审题,然后做出选择。
47.C
【分析】根据题干可知,2红3黄1黑6个珠子一循环,要想知道第48颗珠子是什么颜色,只要知道48÷6后的余数是几,然后分析即可。
【详解】48÷6=8(个)
第48颗珠子是第8组最后一个黑色;
故答案为:C
【点睛】本题主要考查简单周期现象中的规律,找到2红3黄1黑6个珠子一循环是解题的关键。
48.A
【分析】两种相关联的量,如果它们的比值一定,两种量成正比例关系;如果它们的乘积一定,两种量成反比例关系。
【详解】如果=(x、y都不为0),则=,x与y的比值一定,x与y成正比例关系;
如果9∶x=y∶2.3,则xy=20.7,x与y的乘积一定,x与y成反比例关系。
故答案为:A
【点睛】辨识两种量成正比例关系还是成反比例关系,就看它们是比值一定还是乘积一定。
49.C
【分析】将绳长看作单位“1”,已知还剩,则用去了(1-),据此解答即可。
【详解】1-=
>,所以剩下的长。
故答案为:C
【点睛】解决本题需区分两个分数的含义:米是具体的数量,是分率,表示的意义不同。
50.C
【分析】根据“左面砝码数量×砝码位置到中间的距离=右面砝码的数量×砝码位置到中间的距离”,带入数据计算即可。
【详解】4×4÷2
=16÷2
=8(kg)
故答案为:C
【点睛】此题主要考查了杠杆原理的应用,要熟练掌握。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
小升初数学真题汇编6(全国通用版)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.(2022·河北保定·统考小升初真题)几个人握手,每两人之间都握手一次,其中小明一共握了5次,大家一共握了( )次。
A.25 B.20 C.15
2.(2022·湖南娄底·统考小升初真题)下列和成正比例关系的是( )。
A. B. C.(>0) D.
3.(2022·湖南岳阳·统考小升初真题)从A地到B地,甲车要行小时,乙车要行1小时,甲车与乙车的速度比是( )。
A.∶1 B.1∶ C.4∶5 D.5∶4
4.(2022·黑龙江哈尔滨·统考小升初真题)下面的说法不正确的是( )。
A.2∶3和0.6∶0.9能组成比例。
B.圆柱的侧面积一定,底面周长和高成正比例。
C.如果甲在乙的东偏南30°方向,则乙在甲的西偏北30°方向。
5.(2022·云南昆明·统考小升初真题)0.5这个数,在下面生活场景中使用最合适的是( )。
A.两本数学书的质量 B.一个书包的价钱
C.一本数学书封面的大小 D.昆明到大理的路程
6.(2022·安徽合肥·统考小升初真题)用、、三张数字卡片,一共可以组成( )个不同的三位数。
A.4 B.6 C.8
7.(2022·安徽合肥·统考小升初真题)某小区中心花园四种树木棵数统计如表。能正确表示表中信息的扇形统计图是( )。
树木类别 柳树 槐树 松树 银杏树
棵数 120 60 30 30
A. B. C.
8.(2022·四川巴中·统考小升初真题)一架飞机从某机场向南偏东40°方向飞行了3200千米,返回时飞机要向( )。
A.南偏东40°方向飞行3200千米 B.西偏北40°方向飞行3200千米
C.南偏西40°方向飞行3200千米 D.北偏西40°方向飞行3200千米
9.(2022·黑龙江齐齐哈尔·统考小升初真题)周长相等的正方形和圆,它们的面积相比,( )。
A.圆的面积大 B.面积一样大 C.正方形的面积大 D.不确定
10.(2022·广西百色·统考小升初真题)一件商品现在的价格比原来降低了15%,也就是说这件商品按( )折出售。
A.一五 B.八五 C.五 D.十五
11.(2022·贵州铜仁·统考小升初真题)下图不能用“的”来表示的是( )。
①②
③④
A.①② B.②④ C.④ D.②③
12.(2022·内蒙古呼伦贝尔·统考小升初真题)A、B、C各代表一个数,已知A-B=8,A+B=14,C=A+A+B,则A、B、C分别等于( )。
A.10、2、22 B.11、3、25 C.11、8、30 D.12、2、26
13.(2022·内蒙古呼伦贝尔·统考小升初真题)一个圆柱与一个圆锥的体积和高分别相等,已知圆柱的底面积是28.26cm2,圆锥的底面积是( )cm2。
A.9 B.9.42 C.14.13 D.84.78
14.(2022·广东梅州·统考小升初真题)下列说法正确的是( )。
A.一批水果重160%吨 B.一条射线长2.2m C.1的倒数是1
15.(2022·云南曲靖·统考小升初真题)当b=( )时,(36-4b)÷8=0。
A.9 B.7 C.8 D.6
16.(2022·湖南怀化·统考小升初真题)一项工程,6天完成工程的,照这样计算,完成余下的工程还需要( )天。
A.24 B.20 C.5
17.(2022·湖南怀化·统考小升初真题)三个连续偶数,第一个是a,最后一个是( )。
A.a+2 B.a+3 C.a+4
18.(2022·辽宁沈阳·统考小升初真题)将如图中的纸环,沿虚线剪开,可以得到( )个纸环。
A.1 B.2 C.3
19.(2022·辽宁沈阳·统考小升初真题)在“用长方形纸卷圆柱”的实践活动中,我们发现用面积相等的长方形卷成不同的圆柱,( )。
A.侧面积相等,体积也相等
B.底面半径越小,体积越小
C.底面半径越小,体积越大
20.(2022·陕西安康·统考小升初真题)把一个棱长2分米的正方体削成一个最大的圆柱,这个圆柱的侧面积是( )。
A.18.84平方分米 B.6.28平方分米 C.3.14平方分米 D.12.56平方分米
21.(2022·河北唐山·统考小升初真题)用三根以下长度的小棒不能围成三角形的是( )。
A.2cm、3cm、4cm B.2cm、2cm、3cm C.2cm、2cm、2cm D.2cm、2cm、4cm
22.(2022·河北唐山·统考小升初真题)小军想用计算器验算567×39的结果是否正确,但计算器的按键9坏掉了。以下几种方法不能正确验算的是( )。
A.567×3×13 B.567×40-40 C.567×40-567 D.567×38+567
23.(2022·江西赣州·统考小升初真题)一个圆柱和一个圆锥等底等高,圆柱的体积比圆锥多6.4立方分米,圆柱的体积是( )立方分米。
A.1.6 B.3.2 C.6.4 D.9.6
24.(2022·吉林白山·统考小升初真题)如果m和n都是非0自然数,m÷n=23,那么m和n的最小公倍数是( )。
A.m B.n C.23 D.无法确定
25.(2022·河南驻马店·校考小升初真题)如图,转盘中有8个数字,现在淘气将飞镖投向转盘,投中( )情况的可能性最大。
A.2的倍数 B.不是3的倍数 C.大于5的数 D.不大于5的数
26.(2022·山东临沂·统考小升初真题)用一块长是8厘米,宽是6厘米的长方形厚纸板,剪出一个最大的正方形,剩下图形的面积是( )平方厘米。
A.12 B.36 C.48
27.(2022·甘肃庆阳·统考小升初真题)花店在银行的北偏西30°方向200m处,那么银行就在花店的( )方向200m处。
A.东偏南30° B.南偏东30° C.西偏北30° D.北偏西30°
28.(2022·甘肃庆阳·统考小升初真题)要反映牛奶中水、蛋白质、脂肪等含量,用( )更合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表
29.(2022·辽宁大连·统考小升初真题)下面四个图形都是由6个同样大的小正方形组成的,不能折叠成正方体的是( )。
A. B. C. D.
30.(2022·甘肃平凉·统考小升初真题)2022年平凉市的银行年利率为4.6%,李华的妈妈在2022年初存了30000元为了给她的儿子在2025年高考结束后旅游使用,则在2025年共取( )元。
A.1980 B.34600 C.31380 D.34140
31.(2022·湖南邵阳·统考小升初真题)把25克盐溶入200克水中制成盐水,盐和盐水质量的比是( )。
A.1∶8 B.1∶9 C.1∶10 D.1∶11
32.(2022·湖南邵阳·统考小升初真题)在下面的图形中,有4条对称轴的是( )。
A.三角形 B.长方形 C.正方形 D.圆形
33.(2022·广东深圳·统考小升初真题)已知三角形一个角是30°,另外两个内角的度数比是1∶4,那么这个三角形是( )。
A.锐角三角形 B.直角三角形
C.等腰直角三角形 D.钝角三角形
34.(2022·广东深圳·统考小升初真题)13.6%去掉百分号后,这个数就( )。
A.扩大为原来的100倍 B.缩小为原来的
C.大小不变 D.无法确定
35.(2022·广东深圳·统考小升初真题)大于0而小于1的数( )。
A.一个也没有 B.无数个 C.有10个 D.以上都不是
36.(2022·广东深圳·统考小升初真题)如图,已知OA=AB=BC=1cm,那么点P在点O的( )处。
A.北偏西30°,20km B.北偏西60°,20km
C.北偏西30°,40km D.北偏西60°,40km
37.(2022·山东枣庄·统考小升初真题)科学家将新冠病毒疫苗检测器按照10∶1的比例尺画在图上,它在图纸上的长度为4厘米,它的实际长度是( )毫米。
A.400 B.40 C.4 D.0.4
38.(2022·山东枣庄·统考小升初真题)用小棒搭房子,搭一间用5根,搭三间用13根,如图,照这样子搭504间房子要用( )根小棒。
A.2015 B.2016 C.2017 D.2018
39.(2022·河南鹤壁·统考小升初真题)体育课上,老师喊的口令是“向后转”,你的身体应该( )。
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转180° D.逆时针旋转180°
40.(2022·陕西汉中·统考小升初真题)下面各数中,与最接近的是( )。
A.0.374 B.0.6 C.0.63 D.65%
41.(2022·四川广安·统考小升初真题)用9个相同的铁圆锥可以熔铸成( )个与其等底等高的圆柱。
A.3 B.6 C.12 D.27
42.(2022·黑龙江鸡西·统考小升初真题)一个角的两条边是两条( )。
A.直线 B.射线 C.线段 D.以上都对
43.(2022·黑龙江鸡西·统考小升初真题)下面属于方程的是( )。
A.x+5 B.5+6=11 C.x-10=3 D.x÷12>20
44.(2022·辽宁鞍山·统考小升初真题)如图,一个圆锥体酒杯,倒入一些红酒,红酒深为圆锥高的一半,满杯红酒的体积是现在杯中红酒体积的( )倍。
A.2 B.3 C.4 D.8
45.(2022·河北石家庄·统考小升初真题)有30个小球,其中有一个是次品比其它小球轻一些。用天平称重的方法至少( )次一定能找出次品。
A.3 B.4 C.5
46.(2022·江苏南京·统考小升初真题)小明所在班级学生平均身高是1.41米,小强所在班级学生平均身高是1.4米,小明和小强相比( )。
A.小明高 B.小强高 C.一样高 D.无法确定谁高
47.(2022·河南商丘·统考小升初真题)有一串彩色珠子,按2红3黄1黑的顺序排列,第48颗珠子是( )色。
A.红 B.黄 C.黑
48.(2022·河南商丘·统考小升初真题)如果=(x、y都不为0),那么x和y( ),如果9∶x=y∶2.3,那么x和y( )。
A.成正比例;成反比例 B.成反比例;成正比例 C.不成比例;成正比例
49.(2022·河北邯郸·统考小升初真题)一条绳子剪去米,还剩,那么剪去部分和剩下部分相比,( )。
A.剪去的长 B.一样长 C.剩下的长 D.无法确定
50.(2022·山西晋中·统考小升初真题)有一个平衡支架,(如图)在支架左右两边各挂一个质量相同的袋子,右边袋子里放( )kg的物体,支架才能保持平衡。
A.4 B.6 C.8
参考答案:
1.C
【分析】每两人握一次手,小明一共握了5次,即每人都要和其他5人握一次手,那么一共有6个人,共握手(5×6)次,握手是在两人之间进行的,要去掉重复计算的次数,最后结果除以2,据此解答。
【详解】5+1=6(人)
5×6÷2
=30÷2
=15(次)
所以,大家一共握了15次。
故答案为:C
【点睛】本题主要考查搭配问题,解题时也可以用枚举法解答,注意去掉重复计算的情况是解答题目的关键。
2.B
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例;如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.,和一定,与不成比例;
B.,则,比值一定,与成正比例关系;
C.,则,乘积一定,与成反比例关系;
D.,差一定,与不成比例。
故答案为:B
【点睛】掌握正、反比例的意义及辨识方法是解题的关键。
3.D
【分析】把甲、乙两地的路程看成“1”,根据“速度=路程÷时间”,分别写出甲、乙两车的速度,再根据比的意义,即可写出甲车与乙车的速度比,并化成最简整数比。
【详解】(1÷)∶(1÷1)
=∶1
=5∶4
故答案为:D
【点睛】此题是考查比的意义与化简。关键是根据路程、时间、速度三者之间的关系,分别求出甲、乙两车的速度。
4.B
【分析】(1)根据比例的意义:表示两个比相等的式子,分别化简每一组比,再看它们的比值是否相等即可;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,即可解答;
(3)根据位置的相对性可知,它们的方向相反,角度相等,据此解答。
【详解】A.2∶3=,0.6∶0.9=,比值相等,2∶3和0.6∶0.9能组成比例,原题说法正确;
B.圆柱的底面周长×高=侧面积(一定),乘积一定,所以它的底面周长和高成反比例,原题说法错误;
C.如果甲在乙的东偏南30°方向,则乙在甲的西偏北30°方向,原题的说法正确。
故答案为:B
【点睛】判断成正反比例是本题的一个难点,需要熟悉其中的数量关系,以及正反比例的辨识方法。
5.A
【分析】根据生活经验以及对质量单位、长度单位、人民币单位和数据大小的认识,结合实际情况进行选择即可,据此解答。
【详解】两本数学书的质量可以为0.5kg。
故答案为:A
【点睛】解决本题要注意联系生活实际、计量单位和数据的大小,灵活选择。
6.A
【分析】0不能在最高位,先排百位有2种选择,再排十位有2种选择,然后排个位有1种选择,然后根据乘法原理解答即可。
【详解】2×2×1=4(个)
故答案为:A
【点睛】本题考查了乘法原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×m3×……×mn种不同的方法。
7.C
【分析】把四种树木棵数的总数看作单位“1”,根据求一个数是另一个数的百分之几,分别求出四种树所占的分率,然后与下面3幅统计图进行比较即可。
【详解】120+60+30+30=240(课)
柳树:120÷240×100%=50%
槐树:60÷240×100%=25%
松树:30÷240×100%=12.5%
银杏树:30÷240×100%=12.5%
据此可知;柳树要占一半,而松树和银杏数是相等的,只有C选项符合题意。
故答案为:C
【点睛】考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
8.D
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
【详解】一架飞机从某机场向南偏东40°方向飞行了3200千米,返回时飞机要向北偏西40°方向飞行3200千米。
故答案为:D
【点睛】本题主要考查了学生对位置相对性的掌握情况,画图可以帮助理解。
9.A
【分析】假设出它们的周长,根据它们的周长求出正方形的边长和圆的半径,最后利用“”“”求出正方形和圆的面积,并比较大小。
【详解】假设它们的周长为6.28。
正方形的面积:(6.28÷4)×(6.28÷4)
=1.57×1.57
=2.4649
圆的面积:3.14×(6.28÷3.14÷2)2
=3.14×(2÷2)2
=3.14×1
=3.14
因为3.14>2.4649,所以圆的面积大。
故答案为:A
【点睛】掌握正方形和圆的周长和面积的计算公式是解答题目的关键。
10.B
【分析】把原价看成单位“1”,比原来降低了15%,也就是按(1﹣15%)出售的,根据折扣与百分数的关系:几折就表示百分之几十,据此解答。
【详解】1-15%=85%
85%也就是八五折,所以这件商品按八五折出售。
故答案为:B
【点睛】解答本题的关键是理解百分数与折扣的关系。
11.B
【分析】①把长方形平均分成5份,涂其中的3份,表示;然后再把,平均分成3份,涂其中的1份,表示为的,用分数表示为×;
②把整条线段看作单位“1”,平均分成3份,取其中的1份,表示,然后再把平均分成5份,取其中的3份,表示为“的”,用分数表示为×;
③把所有图形看作单位“1”,平均分成5份,涂其中的3份,表示;然后再把,平均分成3份,涂其中的1份,表示为的,用分数表示为;
④把整个长方形看作单位“1”,平均分成10份,涂其中的2份,表示;约分后是,但并不能用表示。
【详解】根据分析得,不能用“的”来表示的是②④。
故答案为:B
【点睛】本题主要考查分数乘法的意义及作图,关键是分清平均分成的份数及取的份数。
12.B
【分析】根据A-B=8,可得A=B+8,将其代入A+B=14中,可得到B的值,进而求出A和C的值。
【详解】根据分析得,把A=B+8代入A+B=14中
可得:B+8+B=14
2B=14-8
2B=6
B=3
A=8+3=11;
C=11+11+3=25。
故答案为:B
【点睛】此题主要考查了简单的等量代换问题,要熟练掌握。再运用等式的性质求出A、B、C的值。
13.D
【分析】圆柱体体积公式V=sh,圆锥体体积公式V=sh,当圆柱体和圆锥体的体积和高都相等时,圆锥体的底面积是圆柱体底面积的3倍。
【详解】28.26×3=84.78(cm2)
故答案为:D
【点睛】解答此题主要根据等底等高的圆锥体的体积是圆柱体体积的,当圆柱体与圆锥体等高等体积时,圆锥体的底面积是圆柱体底面积的3倍。
14.C
【分析】百分数是表示一个数占另一个数的百分比,不能加单位;射线向一端无限延长,不能测量长度;1的倒数是1,据此选择。
【详解】A.百分数后面不能加单位,原题说法错误;
B.射线不能测量长度,原题说法错误;
C.1的倒数是1,原题说法正确。
故答案为:C
【点睛】本题考查了百分数的意义、倒数的意义及射线的特征。
15.A
【分析】根据题意,可列出方程(36-4b)÷8=0,解方程即可得出结论。
【详解】(36-4b)÷8=0
解:(36-4b)÷8×8=0×8
36-4b=0
36-4b+4b=0+4b
4b=36
4b÷4=36÷4
b=9
故答案为:A
【点睛】本题考查的是解方程,要利用等式的性质。
16.A
【分析】把这项工程的工作总量看作单位“1”,用6天除以,可以计算出完成这项工程共需要多少天,再用完成这项工程共需要的天数减去6,可以计算出完成余下的工程还需要多少天。
【详解】
=30-6
=24(天)
故答案为:A
【点睛】本题解题关键是把这项工程的工作总量看作单位“1”,根据分数除法的意义,先计算出完成这项工程共需要多少天,再用减法计算出完成余下的工程还需要多少天。
17.C
【分析】根据2的倍数叫做偶数,又叫做双数即可解答。
【详解】三个连续偶数,第一个是a,最后一个是a+4。
故答案为:C
【点睛】本题考查偶数的概念,2的倍数叫偶数,相邻偶数的差是2。
18.A
【分析】莫比乌斯带:拿一张白的长纸条,把一面涂成黑色,然后把其中一端翻一个身,粘成一个莫比乌斯带,用剪刀沿纸带的中央把它剪开。纸带不仅没有一分为二,反而剪出一个两倍长的纸环;由此求解。
【详解】将图中的纸环,沿虚线剪开,可以得到一个两倍长的纸环。
故答案为:A
【点睛】熟知莫比乌斯带的特点是解决本题的关键。
19.B
【分析】根据圆柱的体积公式:V=πr2h,在“用长方形纸卷圆柱”的实践活动中,我们发现用面积相等的长方形卷成不同的圆柱,底面半径越小,体积就越小。据此解答即可。
【详解】根据分析可知,在“用长方形纸卷圆柱”的实践活动中,我们发现用面积相等的长方形卷成不同的圆柱,底面半径越小,体积就越小。
故答案为:B
【点睛】本题考查的目的是理解掌握圆柱体积的意义及应用。
20.D
【分析】根据题意,棱长是2分米的正方体木块,削成一个最大的圆柱,则它的直径为2分米,高也为2分米,根据圆柱的侧面积公式S=Ch,计算即可解答。
【详解】3.14×2×2
=6.28×2
=12.56(平方分米)
故答案为:D
【点睛】根据题意,把正方体削成一个最大的圆柱,则它的直径为原来的正方体的棱长,高也为正方体的棱长,再根据圆柱的侧面积公式计算即可。
21.D
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【详解】A.2cm+3cm>4cm,能围成三角形;
B.2cm+2cm>3cm,能围成三角形;
C.2cm+2cm>2cm,能围成三角形;
D.2cm+2cm=4cm,不能围成三角形。
故答案为:D
【点睛】本题考查了三角形的三边关系的应用。
22.B
【分析】用计算器验算“567×39”,可是计算器中“9”的按键坏了,那么可以把39分解成两个数的和或差,用乘法分配律进行转换,或者把39分解成两个数的积,再运用乘法结合律把算式转换,从而解决问题。
【详解】A.根据乘法结合律可得:
567×39
=567×3×13
本选项能算出正确答案;
B.567×40-40
=40×(567-1)
=40×566
本选项不能算出正确答案;
C.根据乘法分配律可得:
567×39
=567×(40-1)
=567×40-567
本选项能算出正确答案;
D.根据乘法分配律可得:
567×39
=567×(38+1)
=567×38+567
本选项能算出正确答案。
故答案为:B
【点睛】解决本题关键是熟练掌握乘法结合律和乘法分配律。
23.D
【分析】等底等高的圆柱的体积是圆锥体积的3倍,则圆柱的体积看作3份,圆锥的体积看作1份,相差2份,正好是6.4立方分米,据此求出一份是多少,再乘圆柱对应的份数即可。
【详解】6.4÷2×3
=3.2×3
=9.6(立方分米)
故答案为:D
【点睛】熟练掌握等底等高的圆柱的体积和圆锥体积的倍数关系,是解答此题的关键。
24.A
【分析】由m和n都是非0自然数,m÷n=23,可知m和n是倍数关系,根据倍数关系的最小公倍数是较大数,据此解答。
【详解】m÷n=23,可知m和n是倍数关系,所以m和n的最小公倍数是m。
故答案为:A
【点睛】本题主要考查求两个数的最小公倍数的方法,注意倍数关系的最小公倍数是较大数。
25.B
【分析】可逐项列举出每种情况的数字各有多少个,根据个数的具体情况做选择。
【详解】A.2的倍数:2、4、6、8,共有4个;
B.不是3的倍数:1、2、4、5、7、8,共有6个;
C.大于5的数:6、7、8,共有3个;
D.不大于5的数:1、2、3、4、5,共有5个;
6>5>4>3,即投中不是3的倍数这种情况的可能性最大。
故答案为:B
【点睛】在等可能发生的事件中,如果出现该事件的情况较多,我们就说该事件发生的可能性较大。
26.A
【分析】根据题意可知,在这块长方形的纸板,剪出一个最大的正方形,这个正方形的边长等于长方形的宽,剩下图形的长是6厘米,宽是(8-6)厘米,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】6×(8-6)
=6×2
=12(平方厘米)
故答案为:A
【点睛】此题主要考查长方形的分割,关键是熟记公式有关长方形、正方形的面积公式。
27.B
【分析】根据位置的相对性可知:位置相对的两个物体所在的方向相反、角度相同、距离不变;据此解答。
【详解】花店在银行的北偏西30°方向200m处,那么银行就在花店的南偏东30°方向200m处。
故答案为:B
【点睛】本题主要考查位置的相对性,解题时要明确:位置相对的两个物体所在的方向相反、角度相同、距离不变。
28.C
【分析】条形统计图和统计表能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】要反映牛奶中水、蛋白质、脂肪等含量,用扇形统计图更合适。
故答案为:C
【点睛】此题应根据条形统计图、折线统计图、扇形统计图、统计表各自的特点进行解答。
29.A
【分析】根据正方体展开图的11种特征,即可确定哪个图形属于正方体展开图,能折叠成正方体,哪个图形不属于正方体展开图,不能折叠成正方体。
【详解】所给四个图形都是由6个同样大的小正方形组成的,不能折叠成正方体的是。
故答案为:A
【点睛】正方体展开图有11种特征,分四种类型,即:第一种:“1-4-1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3-3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1-3-2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。
30.D
【分析】根据本息和=本金+本金×利率×存期,代入数据解答即可。
【详解】30000+30000×4.6%×(2025-2022)
=30000+4140
=34140(元)
故答案为:D
【点睛】本题考查了存款利息相关问题,公式:本息和=本金+本金×利率×存期。
31.B
【分析】把25克盐溶入200克水中制成盐水,则盐水的质量是(25+200)克,根据比的意义,即可写出盐和盐水的质量比,并化成最简整数比。
【详解】25∶(25+200)
=25∶225
=1∶9
故答案为:B
【点睛】此题是考查比的意义及化简,两数相除又叫两个数的比,化简比根据比的基本性质。
32.C
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。
【详解】A.等腰三角形有1条对称轴,等边三角形有3条对称轴,一般三角形没有对称轴;
B.长方形有2条对称轴;
C.正方形有4条对称轴;
D.圆有无数条对称轴。
故答案为:C
【点睛】此题考查了轴对称的意义及在实际图形当中的运用。
33.D
【分析】先根据三角形的内角和求出剩下的两个角的度数和,再按照比例分配求出另外两个角,即可解答。
【详解】180°-30°=150°
150°×
=150°×
=30°
150°×
=150°×
=120°
90°<120°<180°
这个三角形是钝角三角形。
故答案为:D
【点睛】利用三角形内角和180°,三角形的分类以及按比例分配问题的知识进行解答。
34.A
【分析】13.6%化成小数是0.136,它的小数点向右移动2位是13.6,就是扩大100倍,据此解答。
【详解】13.6%去掉百分号后,这个数就扩大到原来的100倍。
故答案为:A
【点睛】一个数(不等于0)后面添上百分号,这个数就缩小到原来的;一个百分数去掉百分号,这个数就扩大到原来的100倍。
35.B
【分析】大于0而小于1的一位小数有0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9;
大于0小于1的两位小数有:0.11、0.12、0.13、0.14、0.15、0.16、0.17、0.18、0.19、…0.91、0.92、0.93、0.94、0.95、0.96、0.97、0.98、0.99;
大于0小于1的三位小数有:0.101、0.102、…0.997、0.998、0.999;
以此类推,还有符合条件的四位小数、五位小数……。
【详解】根据分析可知:大于0而小于1的数有无数个。
故答案为:B
【点睛】此题考查的目的是理解小数的意义,掌握小数大小比较的方法。
36.D
【分析】圆上的点到圆心的距离处处相等,90°的角被平分成3个相等的角,则每个角为30°。
用方向和距离结合来描述路线时,要注意三个要素:一是观测点(即参照物),二是方向,三是距离。
【详解】OP=OB=20×2=40(千米)
90°÷3×2
=30°×2
=60°
点P在点O的北偏西60°,40km处。
故答案为:D
【点睛】本题考查圆的特征,图上距离和实际距离的换算,根据方向、角度和距离确定物体的位置。
37.C
【分析】图上距离和比例尺已知,利用“实际距离=图上距离÷比例尺”即可求得它的实际距离。
【详解】4÷10=0.4(厘米)
0.4(厘米)=4(毫米)
它的实际长度是4毫米。
故答案为:C
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
38.C
【分析】搭1间房子用5根小棒,即4×1+1;
搭2间房子用9根小棒,即4×2+1;
搭3间房子用13根小棒,即4×3+1;
……
搭504间房子用的小棒数为:4×504+1。
【详解】4×504+1
=2016+1
=2017(根)
故答案为:C
【点睛】本题主要考查数与形结合的规律,找出规律是解题的关键。
39.C
【分析】旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心,由此并结合实际可知:向左或向右转都是旋转了90°,向后转是旋转了180°;向左是逆时针,向右是顺时针,据此解答即可。
【详解】体育课上,老师喊的口令是“向后转”,你的身体应该顺时针旋转180°。
故答案为:C。
【点睛】解答此题的关键是明白:向左或向右转都是旋转了90°,向后转是旋转了180°。
40.C
【分析】将化为小数,再求出与各选项中的数相差多少,找出相差最小的选项。
【详解】=0.625
0.625-0.374=0.251
0.625-0.6=0.025
0.63-0.625=0.005
65%-0.625=0.025
0.005<0.025<0.251
可见各选项的数中,与最接近的是0.63。
故选:C
【点睛】解答此题需要掌握分数、百分数化小数的方法以及比较小数大小的方法。
41.A
【分析】根据圆柱和圆锥的体积公式可知,等底等高的圆柱的体积是圆锥体积的3倍,据此解答即可。
【详解】9÷3=3(个)
用9个相同的铁圆锥可以熔铸成3个与其等底等高的圆柱。
故答案为:A
【点睛】熟练掌握等底等高的圆柱的体积和圆锥体积的倍数关系,是解答此题的关键。
42.B
【详解】从一个顶点引出的两条射线所组成的图形叫做角,所以一个角的两条边是两条射线。
故答案为:B
43.C
【分析】含有未知数的等式叫做方程;由方程的意义可知,方程必须同时满足以下两个条件:(1)是等式;(2)含有未知数;两个条件缺一不可,据此逐项分析后再选择。
【详解】A.x+5,虽然含有未知数,但它不是等式,所以不是方程;
B.5+6=11,虽然是等式,但它没含有未知数,所以不是方程;
C.x-10=3,既含有未知数,又是等式,符合方程需要满足的两个条件,所以是方程;
D.x÷12>20,虽然含有未知数,但它不是等式,所以不是方程。
故答案为:C
【点睛】此题主要根据方程需要满足的条件来辨识方程,明确只有含有未知数的等式才是方程。
44.D
【分析】根据圆锥的体积公式:V=πr2h,设大圆锥的底面半径为r,高为h,则小圆锥的底面半径为r,高为h,把数据代入公式求出大小圆锥的体积,再根据求一个数是另一个数的几倍,用除法解答。
【详解】解:设大圆锥的底面半径为r,高为h,则小圆锥的底面半径为r,高为h;
πr2h÷[π×(r)2×h]
=πr2h÷[π×r2×h]
=πr2h÷[π×r2h]
=8
故答案为:D
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
45.B
【分析】要达到次数最少,需要将要识别的物品的数目尽可能均匀的分成三份,然后每次称重时,需要将数目相等的两份放到天平两边称重,不断识别,一直到找到次品为止。据此答题即可。
【详解】第一次,把30个小球平均分成3份:10,10,10,任取两份分别放在天平两侧,若天平平衡,较轻的那个小球在未取的一份中,若天平不平衡,取较轻的一份继续;
第二次,取较轻的一份10个小球分成三份,3,3,4,取3个小球的两份分别放在天平两侧,若天平平衡,较轻的那个小球在未取的一份中,若天平不平衡,取较轻的一份继续;
第三次,取较轻的一份(3或4),取2个小球分别放在天平两侧,若天平平衡,较轻的那个是未取的那个小球或在未取的一份中,若天平不平衡,较轻一端是要找的那个小球;
第四次,取较轻的一份2个分别放在天平两侧,较轻一端是略轻的那个小球;
所以用天平称重的方法至少4次一定能找出次品。
故答案为:B
【点睛】解答此题的关键是将所给物品进行合理的分组,逐次称量,即可找出次品。
46.D
【分析】要判断小明和小强的高矮,根据“平均数=总身高÷全班总人数”,平均身高和总身高、总人数有关,并不能代表一个人的身高,由此可得,两个人的身高都不确定,故不能进行比较。
【详解】小明所在班级学生平均身高是1.41米,并不能代表小明的具体身高是1.41米;
小强所在班级学生平均身高是1.4米,并不能代表小强的平均身高是1.4米;
所以小明和小强相比,无法确定谁高。
故答案为:D
【点睛】此题主要考查对平均数的基础知识的掌握情况,做题时一定要弄清题意,认真审题,然后做出选择。
47.C
【分析】根据题干可知,2红3黄1黑6个珠子一循环,要想知道第48颗珠子是什么颜色,只要知道48÷6后的余数是几,然后分析即可。
【详解】48÷6=8(个)
第48颗珠子是第8组最后一个黑色;
故答案为:C
【点睛】本题主要考查简单周期现象中的规律,找到2红3黄1黑6个珠子一循环是解题的关键。
48.A
【分析】两种相关联的量,如果它们的比值一定,两种量成正比例关系;如果它们的乘积一定,两种量成反比例关系。
【详解】如果=(x、y都不为0),则=,x与y的比值一定,x与y成正比例关系;
如果9∶x=y∶2.3,则xy=20.7,x与y的乘积一定,x与y成反比例关系。
故答案为:A
【点睛】辨识两种量成正比例关系还是成反比例关系,就看它们是比值一定还是乘积一定。
49.C
【分析】将绳长看作单位“1”,已知还剩,则用去了(1-),据此解答即可。
【详解】1-=
>,所以剩下的长。
故答案为:C
【点睛】解决本题需区分两个分数的含义:米是具体的数量,是分率,表示的意义不同。
50.C
【分析】根据“左面砝码数量×砝码位置到中间的距离=右面砝码的数量×砝码位置到中间的距离”,带入数据计算即可。
【详解】4×4÷2
=16÷2
=8(kg)
故答案为:C
【点睛】此题主要考查了杠杆原理的应用,要熟练掌握。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
