人教版七年级上册 4.3.2 角的比较与运算 课件(共15张PPT)
文档属性
| 名称 | 人教版七年级上册 4.3.2 角的比较与运算 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 501.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 11:12:37 | ||
图片预览

文档简介
(共15张PPT)
4.3.2 角的比较与运算
O
B
A
B′
(O′)
(A′)
O
B
A
B′
(O′)
(A′)
A
O
B
(A′)
(O′)
(B′)
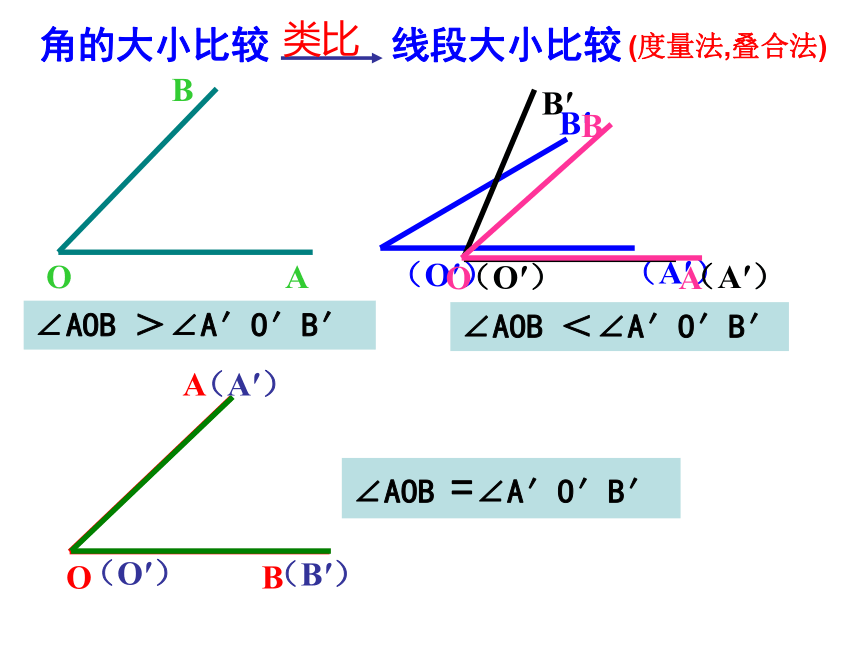
∠AOB >∠A′O′B′
∠AOB <∠A′O′B′
∠AOB =∠A′O′B′
线段大小比较
角的大小比较
类比
(度量法,叠合法)
O
A
C
B
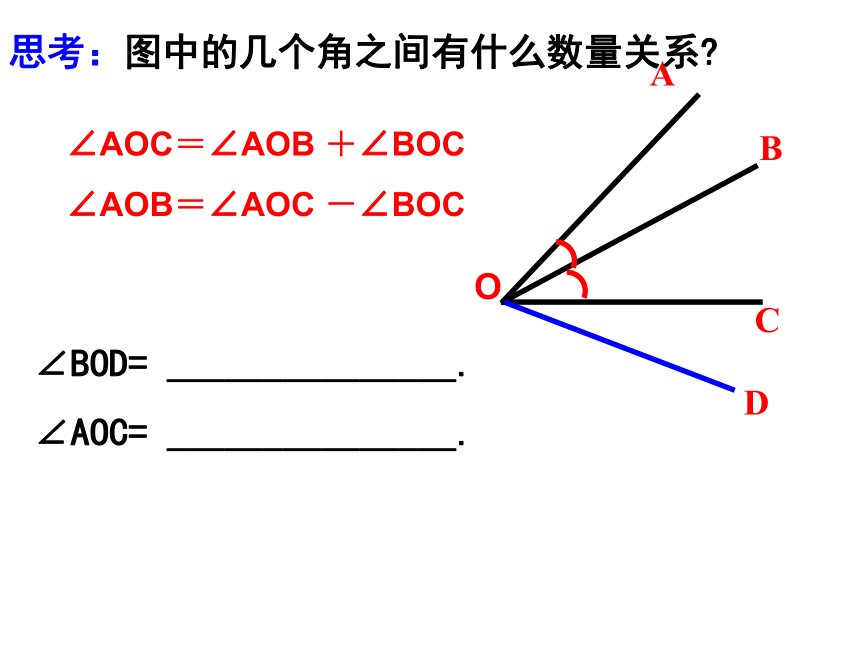
思考:图中的几个角之间有什么数量关系
∠AOC=∠AOB +∠BOC
∠AOB=∠AOC -∠BOC
D
∠BOD= _______________.
∠AOC= _______________.
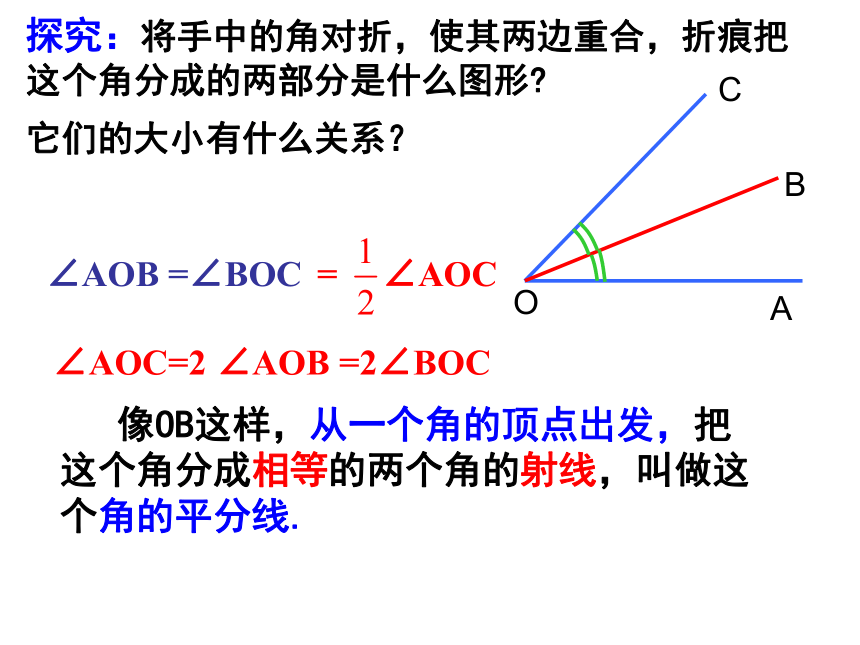
探究:将手中的角对折,使其两边重合,折痕把这个角分成的两部分是什么图形
∠AOB =∠BOC
像OB这样,从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
O
C
B
A
= ∠AOC
∠AOC=2 ∠AOB =2∠BOC
它们的大小有什么关系?
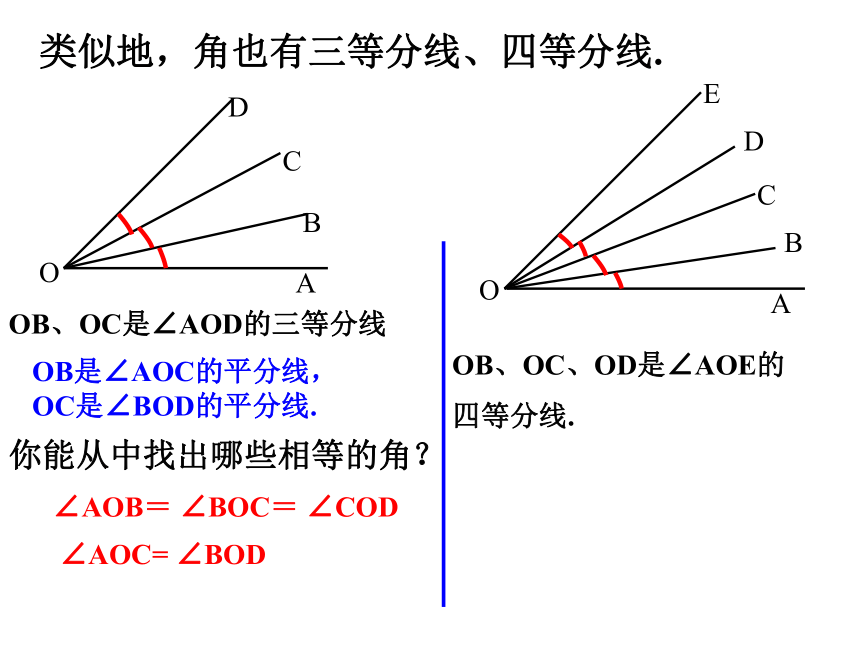
类似地,角也有三等分线、四等分线.
OB、OC是∠AOD的三等分线
A
B
C
D
O
O
A
B
C
D
E
OB、OC、OD是∠AOE的
四等分线.
你能从中找出哪些相等的角?
OB是∠AOC的平分线,OC是∠BOD的平分线.
∠AOB= ∠BOC= ∠COD
∠AOC= ∠BOD
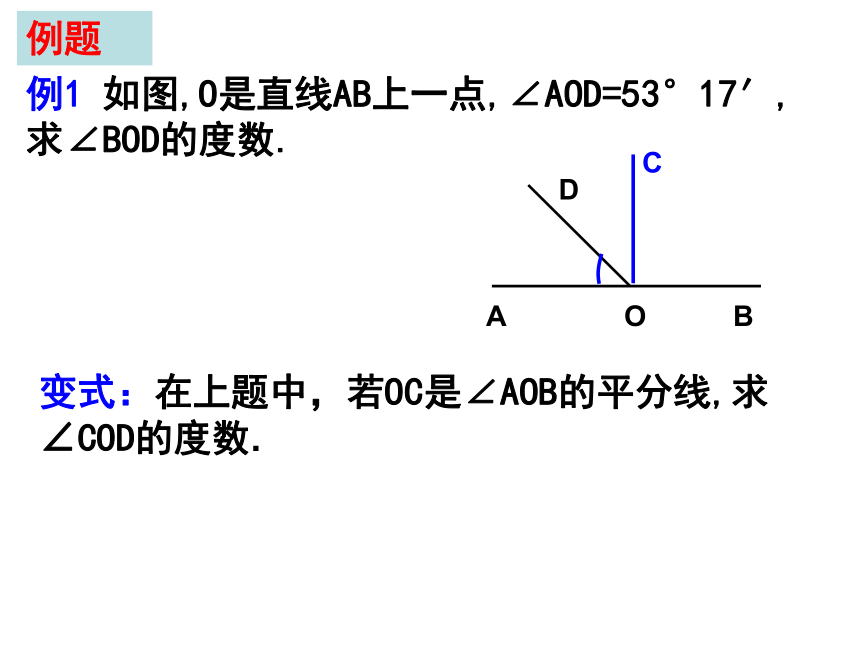
例1 如图,O是直线AB上一点,∠AOD=53°17′,求∠BOD的度数.
O
A
D
B
变式:在上题中,若OC是∠AOB的平分线,求∠COD的度数.
C
例题
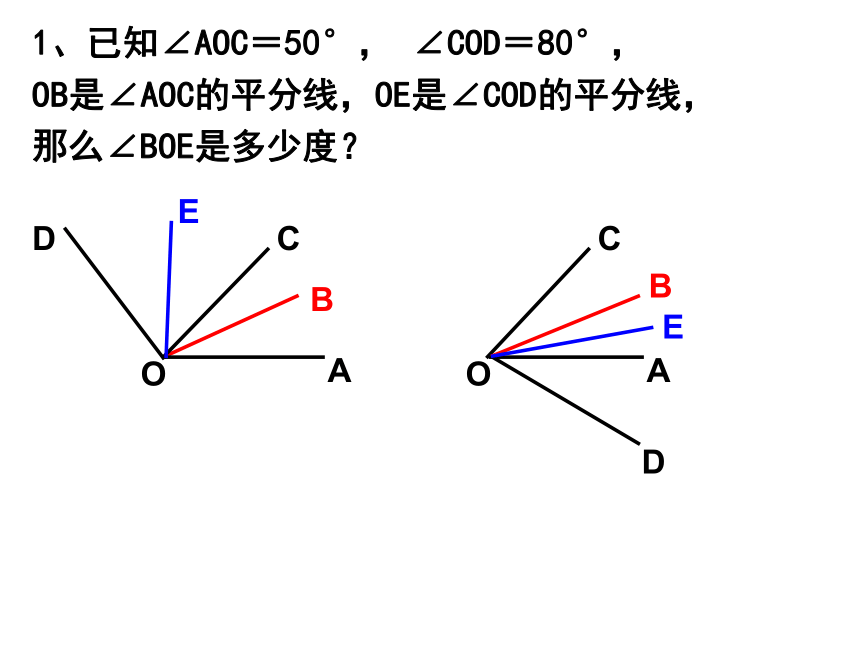
1、已知∠AOC=50°, ∠COD=80°,
OB是∠AOC的平分线,OE是∠COD的平分线,
那么∠BOE是多少度?
B
A
C
O
E
D
A
C
O
D
B
E
2、如图, ∠BOC = ∠AOC, ∠AOB= 144°,求 ∠AOC、 ∠BOC的度数
O
B
C
A
变式:
(1)若 ∠AOB的平分线为OD,
求∠DOC的度数.
D
(2)若 OE平分∠COB,求∠AOE的度数.
E
(3)在以上条件中,求∠DOE的度数.
1.填空:
(1)∠AOC=∠AOB+∠_______;
(2)∠BOD=∠COD+∠_______;
(3)∠AOC=∠AOD-∠_______;
(4)∠BOC=∠______-∠______-∠_____;
(5)∠BOC=∠AOC+∠BOD-∠_______.
BOC
BOC
COD
AOD
AOB
COD
AOD
2.已知∠ABC=30°,BD是∠ABC的平分线,则∠ABD=______度.
15
B
5. 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
(1)求∠EOF的度数;
(2)若∠AOC=x°,∠EOF=y°.则请用x的代数式来表示y;
(3)如果∠AOC+∠EOF=156°,则∠EOF是多少度?
小结:
1、与线段大小比较的方法一样,角的大小比较常用也有两种方法:度量法与叠合法。
2、线段大小比较
角的大小比较
类比
数学知识之间、数学知识与现实世界之间都是密切相关的,只要大家平时多观察、多动手、多思考,知识就在身边。
你会比较两个角的大小吗?
如何比较两条线段的大小 ?
1.度量法
①用刻度尺测量长度;
②根据长度比较大小,
长度大的线段大.
②根据度数判断大小,
度数大的角大.
①用量角器测量度数;
1.度量法
2.叠合法
2.叠合法
②叠合;(在同一直线上,放端点同侧)
③看另一端点作判断。
①对端点;(使一个端点重合)
②对一边,叠合;(放一边同侧)
③看另一边的位置作判断。
①对顶点;(使角的顶点重合)
类比思想
1、如图,一个齿轮有22个齿,每相邻两
齿中心线间的夹角都相等,这个夹角
是多少度
α
练习
(精确到分)
4.3.2 角的比较与运算
O
B
A
B′
(O′)
(A′)
O
B
A
B′
(O′)
(A′)
A
O
B
(A′)
(O′)
(B′)
∠AOB >∠A′O′B′
∠AOB <∠A′O′B′
∠AOB =∠A′O′B′
线段大小比较
角的大小比较
类比
(度量法,叠合法)
O
A
C
B
思考:图中的几个角之间有什么数量关系
∠AOC=∠AOB +∠BOC
∠AOB=∠AOC -∠BOC
D
∠BOD= _______________.
∠AOC= _______________.
探究:将手中的角对折,使其两边重合,折痕把这个角分成的两部分是什么图形
∠AOB =∠BOC
像OB这样,从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
O
C
B
A
= ∠AOC
∠AOC=2 ∠AOB =2∠BOC
它们的大小有什么关系?
类似地,角也有三等分线、四等分线.
OB、OC是∠AOD的三等分线
A
B
C
D
O
O
A
B
C
D
E
OB、OC、OD是∠AOE的
四等分线.
你能从中找出哪些相等的角?
OB是∠AOC的平分线,OC是∠BOD的平分线.
∠AOB= ∠BOC= ∠COD
∠AOC= ∠BOD
例1 如图,O是直线AB上一点,∠AOD=53°17′,求∠BOD的度数.
O
A
D
B
变式:在上题中,若OC是∠AOB的平分线,求∠COD的度数.
C
例题
1、已知∠AOC=50°, ∠COD=80°,
OB是∠AOC的平分线,OE是∠COD的平分线,
那么∠BOE是多少度?
B
A
C
O
E
D
A
C
O
D
B
E
2、如图, ∠BOC = ∠AOC, ∠AOB= 144°,求 ∠AOC、 ∠BOC的度数
O
B
C
A
变式:
(1)若 ∠AOB的平分线为OD,
求∠DOC的度数.
D
(2)若 OE平分∠COB,求∠AOE的度数.
E
(3)在以上条件中,求∠DOE的度数.
1.填空:
(1)∠AOC=∠AOB+∠_______;
(2)∠BOD=∠COD+∠_______;
(3)∠AOC=∠AOD-∠_______;
(4)∠BOC=∠______-∠______-∠_____;
(5)∠BOC=∠AOC+∠BOD-∠_______.
BOC
BOC
COD
AOD
AOB
COD
AOD
2.已知∠ABC=30°,BD是∠ABC的平分线,则∠ABD=______度.
15
B
5. 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
(1)求∠EOF的度数;
(2)若∠AOC=x°,∠EOF=y°.则请用x的代数式来表示y;
(3)如果∠AOC+∠EOF=156°,则∠EOF是多少度?
小结:
1、与线段大小比较的方法一样,角的大小比较常用也有两种方法:度量法与叠合法。
2、线段大小比较
角的大小比较
类比
数学知识之间、数学知识与现实世界之间都是密切相关的,只要大家平时多观察、多动手、多思考,知识就在身边。
你会比较两个角的大小吗?
如何比较两条线段的大小 ?
1.度量法
①用刻度尺测量长度;
②根据长度比较大小,
长度大的线段大.
②根据度数判断大小,
度数大的角大.
①用量角器测量度数;
1.度量法
2.叠合法
2.叠合法
②叠合;(在同一直线上,放端点同侧)
③看另一端点作判断。
①对端点;(使一个端点重合)
②对一边,叠合;(放一边同侧)
③看另一边的位置作判断。
①对顶点;(使角的顶点重合)
类比思想
1、如图,一个齿轮有22个齿,每相邻两
齿中心线间的夹角都相等,这个夹角
是多少度
α
练习
(精确到分)
