山东省青岛市海信中学2022-2023学下学期八年级期中数学试题(图片版 无答案)
文档属性
| 名称 | 山东省青岛市海信中学2022-2023学下学期八年级期中数学试题(图片版 无答案) |  | |
| 格式 | |||
| 文件大小 | 683.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 13:48:19 | ||
图片预览

文档简介
2022-2023学年度第二学期阶段性检测 6.用反证法证明三角形至少有一个角不大于 60°,应假设( )
A.三个角都小于 60° B.三个角都大于 60°
八年级数学试题
C.三个角都大于或等于 60° D.有两个角大于 60° 时间:120 分钟 满分:120 分
真情提示:亲爱的同学们,你们好!你可要冷静思考,沉着答卷,争取有更 7.若不等式组 有解,则 a 的取值范围是( )
加出色的发挥。相信自己一定能行,祝你答题成功!
A.a>﹣1 B.a≥﹣1 C.a≤1 D.a<1
一.选择题
二、不定项选择
1.下列图形中,中心对称图形是( )
8.在等边△ABC 中,D 是边 AC 上一点,连接 BD,将△BCD 绕点 B 逆时针旋转 60°,得到△BAE,
连接 ED,若 BC=5,BD=4,则以下四个结论中:①△BDE 是等边三角形;②AE∥BC;③△ADE
的周长是 9;④∠ADE=∠BDC.其中正确的序号是( )
A.① B.② C.③ D.④
A. B. C. D.
三.填空题(共 8 小题)
2.下列各式从左到右的变形,是因式分解的是( )
9.2020 年 1 月 6 日,《青岛市生活垃圾管理条例》正式实施,该条例倡导绿色、低碳、文明的生活方
A.x2+2x+3=x(x+2)+3 B.(x+1)(x﹣1)=x2﹣1
式,促进全民垃圾分类意识的提升,为落实“垃圾分类”的环保理念,某校计划采购一批垃圾桶,
C.y2﹣3y﹣4=(y﹣4)(y+1) D.
已知蓝色垃圾桶的单价是 100 元,灰色垃圾桶的单价是 80 元,学校计划用不超过 4500 元资金购入
3.如图,将等腰三角形纸片沿 DE 折叠,使点 B 与点 A 重合,并且 AC=DC,∠BAC 的度数为( )
两种垃圾桶共 50 个,且蓝色垃圾桶的数量不少于灰色垃圾桶数量的 80%,则至少需采购蓝色垃圾桶
A.120° B.108° C.106° D.100°
个.
10.如图,已知 O 为△ABC 的三边垂直平分线的交点,如果∠A=65°,则∠BOC= °.
第 3 题 第 5 题 第 8 题
4.已知 a<b,下列式子不一定成立的是( )
A.a﹣1<b﹣1 B.﹣2a>﹣2b C.2a+1<2b+1 D.m2a> 2 m b
10 题 11 题 12 题
5.如图,点 A(0,4),△AOB 沿 x 轴向右平移后得到△O′A′B′,点 A 的对应点 A′在直线
11.如图,△ABC 的边 BC 长为 4cm.将△ABC 平移 2cm 得到△A'B'C',且 BB'⊥BC,则阴影部分的面
上,则△AOB 向右平移的长度为( )
积为 cm2.
A. B.10 C.8 D.6
12.如图,在△ABC 中,CD 是△ABC 的角平分线,DE⊥BC 于 E,F,G 分别是边 AC,BC 上的点,
八年级数学试题第 1 页 共 4 页
连接 DF,DG,若 DF=DG,△CDF 和△DEG 的面积分别为 50 和 15,则△CDG 的面积为 . 图,保留作图痕迹,不写作法)
13.如图,在△ABC 中,AB=AC,∠BAC=36°,DE 是线段 AC 的垂直平分线,若 BE=a,AE=b,
则用含 a、b 的代数式表示△ABC 的周长为 .
18.解下列不等式(组).
(1)4x+5≥6x﹣3; (2) ≤1;
(3) ,并写出其整数解.
13 题 14 题
14.如图,在三角板 ABC 中,∠ACB=90°,∠A=30°,AC=6,将三角板 ABC 绕点 C 逆时针旋转, 19.把下列各题因式分解:
当起始位置时的点 B 恰好落在边 A1B1 上时,A1B 的长为 . (1)﹣4xy﹣x
2﹣4y2;
15.如图,∠AOB=30°,点 P 位于∠AOB 内,OP=3,点 M,N 分别是射线 OA、OB 边上的动点,
当△PMN 的周长最小时,最小周长为 . (2)先因式分解,再计算求值: ,其中 m=﹣ ,n=4.
20.化简:
(1) ; (2) .
15 题 16 题
16.在如图所示的平面直角坐标系中,△OA1B1 是边长为 2 的等边三角形,作△B2A2B1 与△OA1B1 关于
点 B1 成中心对称,再作△B2A3B3 与△B2A2B1 关于点 B2 成中心对称,如此作下去,△B2nA2n+1B2n+1
(n 是正整数)的顶点 A2n+1 的坐标是 .
四.解答题(共 10 小题)
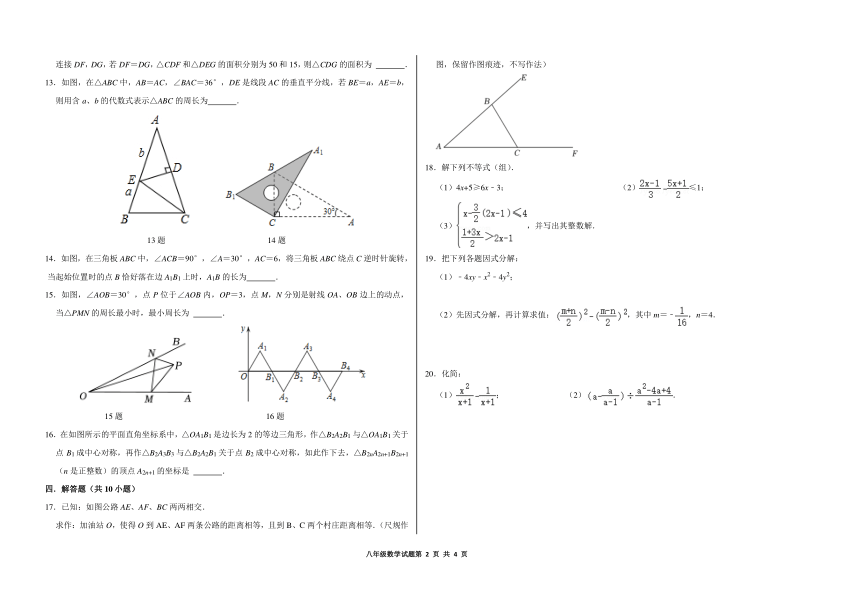
17.已知:如图公路 AE、AF、BC 两两相交.
求作:加油站 O,使得 O 到 AE、AF 两条公路的距离相等,且到 B、C 两个村庄距离相等.(尺规作
八年级数学试题第 2 页 共 4 页
21.在如图所示的直角坐标系中,解答下列问题: 24.如图,在△ABC 中,AB=AC,AD⊥BC 于点 D,E 为 AC 边上一点,连接 BE 与 AD 交于点 F,G
(1)将△ABC 绕点 A 顺时针旋转 90°,画出旋转后的△AB1C1 为△ABC 外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接 EG.
(2)求点 B 的移动路径长. (1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
22.如图,在△ABC 中,∠A=120°,AB=AC,D 是 BC 的中点,DE⊥AB,DF⊥AC,点 E,F 为垂 25.问题提出
足,求证:△DEF 是等边三角形. 我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进
行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利
用差的符号确定它们的大小,即要比较代数式 M、N 的大小,只要作出它们的差 M﹣N,若 M﹣N>
0,则 M>N;若 M﹣N=0,则 M=N;若 M﹣N<0,则 M<N.
问题解决
23.某商场计划购进 A,B 两种新型节能台灯共 100 盏,这两种台灯的进价、售价如下表: 如图 1,把边长为 a+b(a≠b)的大正方形分割成两个边长分别是 a、b 的小正方形及两个矩形,试
类型 价格 进价(元/盏) 售价(元/盏) 比较两个小正方形面积之和 M 与两个矩形面积之和 N 的大小.
A 型 30 45 解:由图可知:M=a
2+b2,N=2ab.
∴M﹣N=a2+b2﹣2ab=(a﹣b)2.
B 型 50 70
∵a≠b,∴(a﹣b)2>0.
(1)若设商场购进 A 型台灯 m 盏,销售完这批台灯所获利润为 P,写出 P 与 m 之间的函数关系式.
∴M﹣N>0.
(2)若商场规定 B 型灯的进货数量不超过 A 型灯数量的 4 倍,那么 A 型和 B 型台灯各进多少盏售
∴M>N.
完之后获得利润最多?此时利润是多少元.
类比应用
(1)已知小丽和小颖购买同一种商品的平均价格分别为 元/千克和 元/千克(a、b 是正数,
八年级数学试题第 3 页 共 4 页
且 a≠b),试比较小丽和小颖所购买商品的平均价格的高低. (3)当 t 为何值时,点 A 在线段 PQ 的垂直平分线上.
(2)试比较图 2 和图 3 中两个矩形周长 M1、N1 的大小(b>c). (4)点 P、Q 在运动的过程中,是否存在某一时刻 t,直线 PQ 把△ABC 的周长与面积同时平分?
若存在,求出 t,若不存在,请说明理由.
联系拓广
小刚在超市里买了一些物品,用一个长方体的箱子“打包”,这个箱子的尺寸如图 4 所示(其中 b>
a>c>0),售货员分别可按图 5、图 6、图 7 三种方法进行捆绑,问哪种方法用绳最短?哪种方法用
绳最长?请说明理由.
26.已知:把一副三角板按如图 1 摆放(点 C 与点 E 重合),点 B、C(E)、F 在同一条直线上.∠ACB
=∠EDF=90°,∠DEF=45°,∠A=30°,BC=6cm,EF=9cm,如图 2,△DEE 从图 1 的位置
出发,以 1cm/s 的速度沿 CB 向△ABC 匀速移动,在△DEF 移动的同时,点 P 从△ABC 的顶点 B 出
发.以 2cm/s 的速度沿 BA 向点 A 匀速移动.当△DEF 的顶点 D 移动到 AC 边上时,△DEF 停止移
动.点 P 也随之停止移动.DE 与 AC 相交于点 Q,连接 PQ,设移动时间为 t(s)(0<t<4.5).解
答下列问题:
(1)用含 t 的代数式表示线段 CQ= ,线段 AP= .
(2)当 t 为何值时,∠BPE=90°.
八年级数学试题第 4 页 共 4 页
A.三个角都小于 60° B.三个角都大于 60°
八年级数学试题
C.三个角都大于或等于 60° D.有两个角大于 60° 时间:120 分钟 满分:120 分
真情提示:亲爱的同学们,你们好!你可要冷静思考,沉着答卷,争取有更 7.若不等式组 有解,则 a 的取值范围是( )
加出色的发挥。相信自己一定能行,祝你答题成功!
A.a>﹣1 B.a≥﹣1 C.a≤1 D.a<1
一.选择题
二、不定项选择
1.下列图形中,中心对称图形是( )
8.在等边△ABC 中,D 是边 AC 上一点,连接 BD,将△BCD 绕点 B 逆时针旋转 60°,得到△BAE,
连接 ED,若 BC=5,BD=4,则以下四个结论中:①△BDE 是等边三角形;②AE∥BC;③△ADE
的周长是 9;④∠ADE=∠BDC.其中正确的序号是( )
A.① B.② C.③ D.④
A. B. C. D.
三.填空题(共 8 小题)
2.下列各式从左到右的变形,是因式分解的是( )
9.2020 年 1 月 6 日,《青岛市生活垃圾管理条例》正式实施,该条例倡导绿色、低碳、文明的生活方
A.x2+2x+3=x(x+2)+3 B.(x+1)(x﹣1)=x2﹣1
式,促进全民垃圾分类意识的提升,为落实“垃圾分类”的环保理念,某校计划采购一批垃圾桶,
C.y2﹣3y﹣4=(y﹣4)(y+1) D.
已知蓝色垃圾桶的单价是 100 元,灰色垃圾桶的单价是 80 元,学校计划用不超过 4500 元资金购入
3.如图,将等腰三角形纸片沿 DE 折叠,使点 B 与点 A 重合,并且 AC=DC,∠BAC 的度数为( )
两种垃圾桶共 50 个,且蓝色垃圾桶的数量不少于灰色垃圾桶数量的 80%,则至少需采购蓝色垃圾桶
A.120° B.108° C.106° D.100°
个.
10.如图,已知 O 为△ABC 的三边垂直平分线的交点,如果∠A=65°,则∠BOC= °.
第 3 题 第 5 题 第 8 题
4.已知 a<b,下列式子不一定成立的是( )
A.a﹣1<b﹣1 B.﹣2a>﹣2b C.2a+1<2b+1 D.m2a> 2 m b
10 题 11 题 12 题
5.如图,点 A(0,4),△AOB 沿 x 轴向右平移后得到△O′A′B′,点 A 的对应点 A′在直线
11.如图,△ABC 的边 BC 长为 4cm.将△ABC 平移 2cm 得到△A'B'C',且 BB'⊥BC,则阴影部分的面
上,则△AOB 向右平移的长度为( )
积为 cm2.
A. B.10 C.8 D.6
12.如图,在△ABC 中,CD 是△ABC 的角平分线,DE⊥BC 于 E,F,G 分别是边 AC,BC 上的点,
八年级数学试题第 1 页 共 4 页
连接 DF,DG,若 DF=DG,△CDF 和△DEG 的面积分别为 50 和 15,则△CDG 的面积为 . 图,保留作图痕迹,不写作法)
13.如图,在△ABC 中,AB=AC,∠BAC=36°,DE 是线段 AC 的垂直平分线,若 BE=a,AE=b,
则用含 a、b 的代数式表示△ABC 的周长为 .
18.解下列不等式(组).
(1)4x+5≥6x﹣3; (2) ≤1;
(3) ,并写出其整数解.
13 题 14 题
14.如图,在三角板 ABC 中,∠ACB=90°,∠A=30°,AC=6,将三角板 ABC 绕点 C 逆时针旋转, 19.把下列各题因式分解:
当起始位置时的点 B 恰好落在边 A1B1 上时,A1B 的长为 . (1)﹣4xy﹣x
2﹣4y2;
15.如图,∠AOB=30°,点 P 位于∠AOB 内,OP=3,点 M,N 分别是射线 OA、OB 边上的动点,
当△PMN 的周长最小时,最小周长为 . (2)先因式分解,再计算求值: ,其中 m=﹣ ,n=4.
20.化简:
(1) ; (2) .
15 题 16 题
16.在如图所示的平面直角坐标系中,△OA1B1 是边长为 2 的等边三角形,作△B2A2B1 与△OA1B1 关于
点 B1 成中心对称,再作△B2A3B3 与△B2A2B1 关于点 B2 成中心对称,如此作下去,△B2nA2n+1B2n+1
(n 是正整数)的顶点 A2n+1 的坐标是 .
四.解答题(共 10 小题)
17.已知:如图公路 AE、AF、BC 两两相交.
求作:加油站 O,使得 O 到 AE、AF 两条公路的距离相等,且到 B、C 两个村庄距离相等.(尺规作
八年级数学试题第 2 页 共 4 页
21.在如图所示的直角坐标系中,解答下列问题: 24.如图,在△ABC 中,AB=AC,AD⊥BC 于点 D,E 为 AC 边上一点,连接 BE 与 AD 交于点 F,G
(1)将△ABC 绕点 A 顺时针旋转 90°,画出旋转后的△AB1C1 为△ABC 外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接 EG.
(2)求点 B 的移动路径长. (1)求证:△ABF≌△ACG;
(2)求证:BE=CG+EG.
22.如图,在△ABC 中,∠A=120°,AB=AC,D 是 BC 的中点,DE⊥AB,DF⊥AC,点 E,F 为垂 25.问题提出
足,求证:△DEF 是等边三角形. 我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进
行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利
用差的符号确定它们的大小,即要比较代数式 M、N 的大小,只要作出它们的差 M﹣N,若 M﹣N>
0,则 M>N;若 M﹣N=0,则 M=N;若 M﹣N<0,则 M<N.
问题解决
23.某商场计划购进 A,B 两种新型节能台灯共 100 盏,这两种台灯的进价、售价如下表: 如图 1,把边长为 a+b(a≠b)的大正方形分割成两个边长分别是 a、b 的小正方形及两个矩形,试
类型 价格 进价(元/盏) 售价(元/盏) 比较两个小正方形面积之和 M 与两个矩形面积之和 N 的大小.
A 型 30 45 解:由图可知:M=a
2+b2,N=2ab.
∴M﹣N=a2+b2﹣2ab=(a﹣b)2.
B 型 50 70
∵a≠b,∴(a﹣b)2>0.
(1)若设商场购进 A 型台灯 m 盏,销售完这批台灯所获利润为 P,写出 P 与 m 之间的函数关系式.
∴M﹣N>0.
(2)若商场规定 B 型灯的进货数量不超过 A 型灯数量的 4 倍,那么 A 型和 B 型台灯各进多少盏售
∴M>N.
完之后获得利润最多?此时利润是多少元.
类比应用
(1)已知小丽和小颖购买同一种商品的平均价格分别为 元/千克和 元/千克(a、b 是正数,
八年级数学试题第 3 页 共 4 页
且 a≠b),试比较小丽和小颖所购买商品的平均价格的高低. (3)当 t 为何值时,点 A 在线段 PQ 的垂直平分线上.
(2)试比较图 2 和图 3 中两个矩形周长 M1、N1 的大小(b>c). (4)点 P、Q 在运动的过程中,是否存在某一时刻 t,直线 PQ 把△ABC 的周长与面积同时平分?
若存在,求出 t,若不存在,请说明理由.
联系拓广
小刚在超市里买了一些物品,用一个长方体的箱子“打包”,这个箱子的尺寸如图 4 所示(其中 b>
a>c>0),售货员分别可按图 5、图 6、图 7 三种方法进行捆绑,问哪种方法用绳最短?哪种方法用
绳最长?请说明理由.
26.已知:把一副三角板按如图 1 摆放(点 C 与点 E 重合),点 B、C(E)、F 在同一条直线上.∠ACB
=∠EDF=90°,∠DEF=45°,∠A=30°,BC=6cm,EF=9cm,如图 2,△DEE 从图 1 的位置
出发,以 1cm/s 的速度沿 CB 向△ABC 匀速移动,在△DEF 移动的同时,点 P 从△ABC 的顶点 B 出
发.以 2cm/s 的速度沿 BA 向点 A 匀速移动.当△DEF 的顶点 D 移动到 AC 边上时,△DEF 停止移
动.点 P 也随之停止移动.DE 与 AC 相交于点 Q,连接 PQ,设移动时间为 t(s)(0<t<4.5).解
答下列问题:
(1)用含 t 的代数式表示线段 CQ= ,线段 AP= .
(2)当 t 为何值时,∠BPE=90°.
八年级数学试题第 4 页 共 4 页
同课章节目录
