图形的旋转
图片预览




文档简介
(共23张PPT)
世界如此美丽
观察:下列图片中,电扇的风叶,时钟的时针、分针在转动的过程中有什么共同特征?
平面内,一个图形绕一个定点转动,像这样的运动我们称它为旋转。
请列举一些日常生活中其它的旋转现象!
图形的旋转
生 活 中 的 旋 转
生 活 中 的 旋 转
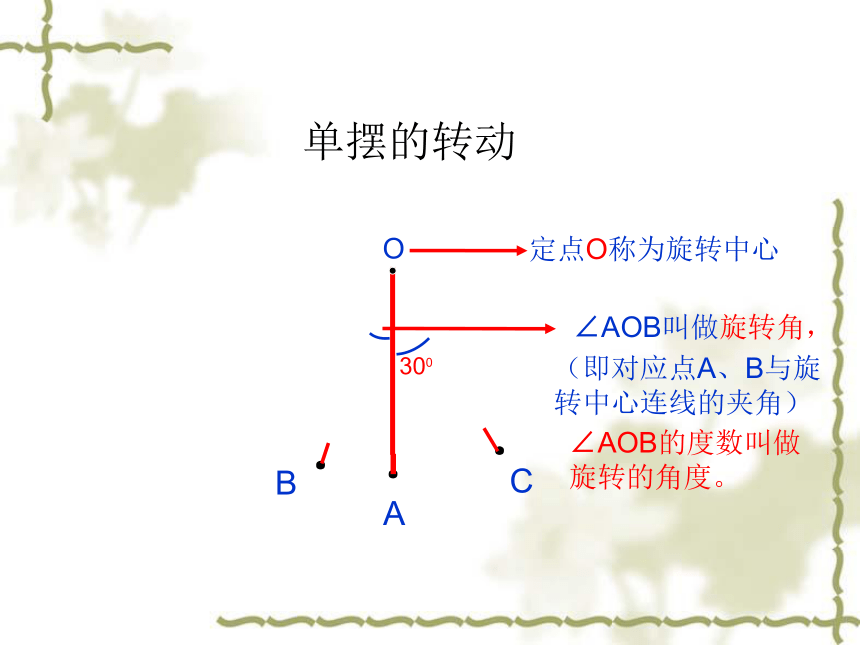
单摆的转动
O
∠AOB叫做旋转角,
定点O称为旋转中心
(即对应点A、B与旋转中心连线的夹角)
∠AOB的度数叫做旋转的角度。
300
A
·
·
B
·
C
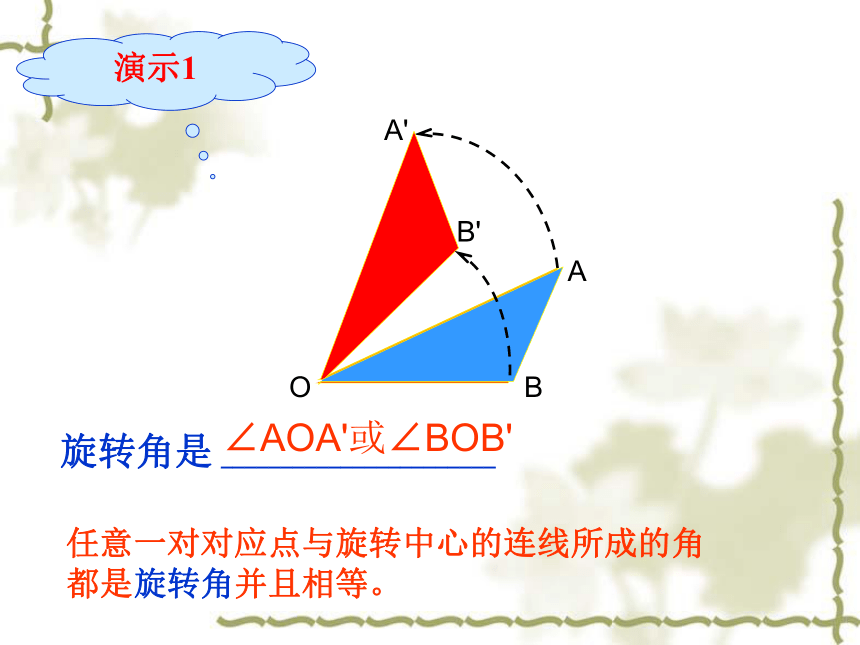
演示1
A'
B'
B
A
O
∠AOA'或∠BOB'
旋转角是 _______________________
任意一对对应点与旋转中心的连线所成的角
都是旋转角并且相等。
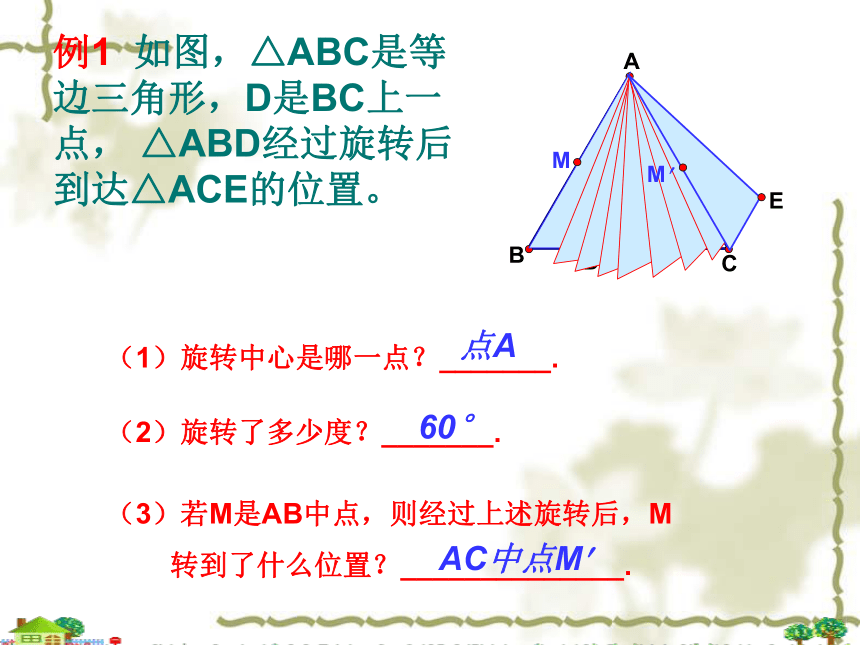
(1)旋转中心是哪一点?_______.
(2)旋转了多少度?_______.
(3)若M是AB中点,则经过上述旋转后,M
转到了什么位置?______________.
点A
60°
AC中点M
例1 如图,△ABC是等边三角形,D是BC上一点, △ABD经过旋转后到达△ACE的位置。
E
C
A
B
D
M
M
A
B
互相垂直。(旋转中心均为点M)
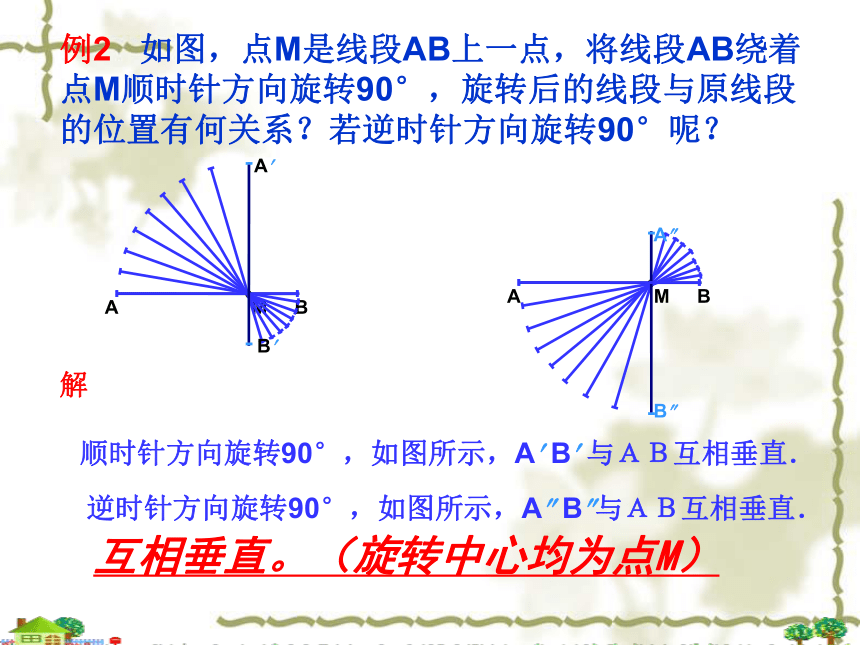
例2 如图,点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90°,旋转后的线段与原线段的位置有何关系?若逆时针方向旋转90°呢?
M
B
A
A
B
M
B
A
解
逆时针方向旋转90°,如图所示,A B 与AB互相垂直.
顺时针方向旋转90°,如图所示,A B 与AB互相垂直.
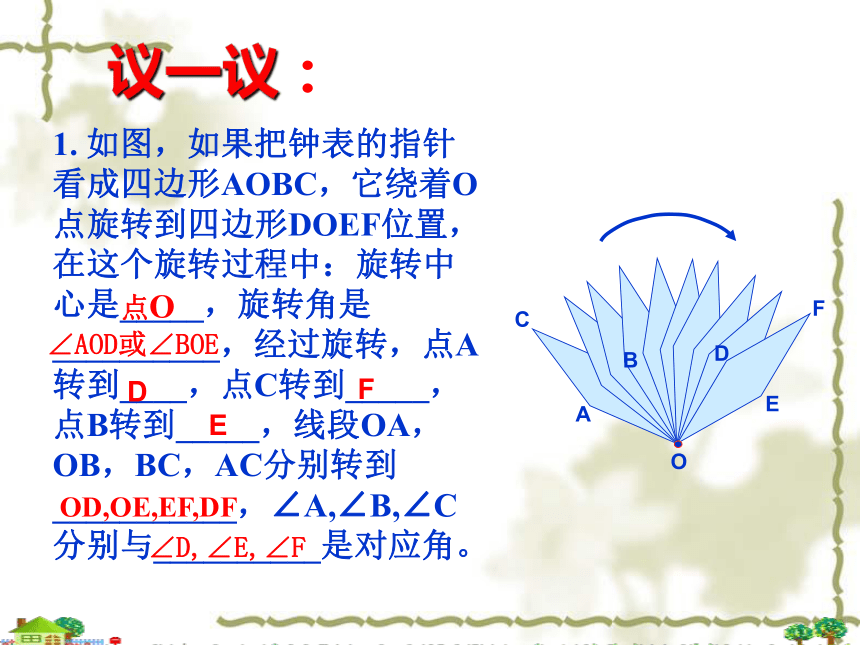
议一议:
C
B
A
O
F
E
D
1. 如图,如果把钟表的指针看成四边形AOBC,它绕着O点旋转到四边形DOEF位置,在这个旋转过程中:旋转中心是_____,旋转角是__________,经过旋转,点A转到____,点C转到_____,点B转到_____,线段OA,OB,BC,AC分别转到___________,∠A,∠B,∠C分别与__________是对应角。
点O
D
F
E
OD,OE,EF,DF
∠AOD或∠BOE
∠D,∠E,∠F
B ____
A ____
∠AOB ______
A
B
∠A OB
用一张半透明的薄纸,覆盖在画有任意△AOB的纸上,在薄纸上画出与△AOB重合的一个三角形,然后用一枚图钉在O处固定,将薄纸绕着图钉(即点O)转动一个角度45°,薄纸上的三角形就旋转到了新的位置,标上A ,O,B .我们可以认为 △AOB旋转45°后变成△A OB 。在旋转过程中,你发现了什么?
45°
A'
B'
O
A
B
试一试:
可以看到点A旋转到点A , OA旋转到OA , ∠AOB旋转到∠A OB ,这些都是互相对应的点、线段与角 .
OA的对应线段是____,OB的对应线段是_____,AB的对应线段是_____; ∠A的对应角是_____,∠B的对应角是______。
此时,
旋转中心是点_____, 旋转角度是_______。
思考: △AOB的边OB的中点D的对应点在哪里?
OA
OB
A B
∠A
∠B
O
45°
在OB 的中点D
45°
A
B
O
A
B
旋转的性质:
(1) 对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于
旋转角;
(3)旋转前、后的图形全等。
如图:P是等边 ABC内的一点,把 ABP按不同的方向通过旋转得到 BQC和 ACR ,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把 BQC旋转得到?
A
Q
R
P
C
B
BQC
ABP
ACR
BQC
ABP
ACR
注意:
(1)本章主要研究基本的平面图形在平面内的旋转;
(2)旋转中心在旋转过程中保持不动;
(3)旋转过程静止时,图形上每一点的旋转角是一样的,旋转角度一般小于360度.
(4) 旋转,除了表示物体的转动以外,还可以作为名词来用,即两个图形可以存在旋转关系。同平移一样,旋转也可以组成优美的图案。
小结
今天,我们认识了除轴对称、平移以外的第三种变换:旋转.它和平移有类似之处,也有不同之处.旋转的因素有两个:旋转中心与旋转角度.旋转正是由它们决定的.旋转时物体大小不变、形状不变,但位置变了.旋转同样要找准对应点、角、线段.
演示2
O
O
B
A
C
O
B
C
A
O
O
∠ BOB 、∠AOA 、 ∠ COC
旋转角是___________________________。
演示3
B
A
C
O
B
C
A
旋转角是___________________________。
∠ BOB 、∠AOA 、 ∠ COC
精心做一做
如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
(1)旋转中心是哪一点
(2) 旋转了多少度
(3)如果点G是AB的中点,那么经过上述旋转后,点G到了什么位置
点A
900
A
B
F
C
E
G.
D
.G
(4) 连结EF,那么△AEF是怎样的三角形
本节课我们主要学了什么内容?
旋转的概念:平面内,将一个图形绕着一个定点转动,这样的图形运动称为旋转。
决定旋转的三个要素
旋转中心
旋转方向
旋转角度
通过这节课的学习谈谈你的感想。
世界如此美丽
观察:下列图片中,电扇的风叶,时钟的时针、分针在转动的过程中有什么共同特征?
平面内,一个图形绕一个定点转动,像这样的运动我们称它为旋转。
请列举一些日常生活中其它的旋转现象!
图形的旋转
生 活 中 的 旋 转
生 活 中 的 旋 转
单摆的转动
O
∠AOB叫做旋转角,
定点O称为旋转中心
(即对应点A、B与旋转中心连线的夹角)
∠AOB的度数叫做旋转的角度。
300
A
·
·
B
·
C
演示1
A'
B'
B
A
O
∠AOA'或∠BOB'
旋转角是 _______________________
任意一对对应点与旋转中心的连线所成的角
都是旋转角并且相等。
(1)旋转中心是哪一点?_______.
(2)旋转了多少度?_______.
(3)若M是AB中点,则经过上述旋转后,M
转到了什么位置?______________.
点A
60°
AC中点M
例1 如图,△ABC是等边三角形,D是BC上一点, △ABD经过旋转后到达△ACE的位置。
E
C
A
B
D
M
M
A
B
互相垂直。(旋转中心均为点M)
例2 如图,点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90°,旋转后的线段与原线段的位置有何关系?若逆时针方向旋转90°呢?
M
B
A
A
B
M
B
A
解
逆时针方向旋转90°,如图所示,A B 与AB互相垂直.
顺时针方向旋转90°,如图所示,A B 与AB互相垂直.
议一议:
C
B
A
O
F
E
D
1. 如图,如果把钟表的指针看成四边形AOBC,它绕着O点旋转到四边形DOEF位置,在这个旋转过程中:旋转中心是_____,旋转角是__________,经过旋转,点A转到____,点C转到_____,点B转到_____,线段OA,OB,BC,AC分别转到___________,∠A,∠B,∠C分别与__________是对应角。
点O
D
F
E
OD,OE,EF,DF
∠AOD或∠BOE
∠D,∠E,∠F
B ____
A ____
∠AOB ______
A
B
∠A OB
用一张半透明的薄纸,覆盖在画有任意△AOB的纸上,在薄纸上画出与△AOB重合的一个三角形,然后用一枚图钉在O处固定,将薄纸绕着图钉(即点O)转动一个角度45°,薄纸上的三角形就旋转到了新的位置,标上A ,O,B .我们可以认为 △AOB旋转45°后变成△A OB 。在旋转过程中,你发现了什么?
45°
A'
B'
O
A
B
试一试:
可以看到点A旋转到点A , OA旋转到OA , ∠AOB旋转到∠A OB ,这些都是互相对应的点、线段与角 .
OA的对应线段是____,OB的对应线段是_____,AB的对应线段是_____; ∠A的对应角是_____,∠B的对应角是______。
此时,
旋转中心是点_____, 旋转角度是_______。
思考: △AOB的边OB的中点D的对应点在哪里?
OA
OB
A B
∠A
∠B
O
45°
在OB 的中点D
45°
A
B
O
A
B
旋转的性质:
(1) 对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于
旋转角;
(3)旋转前、后的图形全等。
如图:P是等边 ABC内的一点,把 ABP按不同的方向通过旋转得到 BQC和 ACR ,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ACR是否可以直接通过把 BQC旋转得到?
A
Q
R
P
C
B
BQC
ABP
ACR
BQC
ABP
ACR
注意:
(1)本章主要研究基本的平面图形在平面内的旋转;
(2)旋转中心在旋转过程中保持不动;
(3)旋转过程静止时,图形上每一点的旋转角是一样的,旋转角度一般小于360度.
(4) 旋转,除了表示物体的转动以外,还可以作为名词来用,即两个图形可以存在旋转关系。同平移一样,旋转也可以组成优美的图案。
小结
今天,我们认识了除轴对称、平移以外的第三种变换:旋转.它和平移有类似之处,也有不同之处.旋转的因素有两个:旋转中心与旋转角度.旋转正是由它们决定的.旋转时物体大小不变、形状不变,但位置变了.旋转同样要找准对应点、角、线段.
演示2
O
O
B
A
C
O
B
C
A
O
O
∠ BOB 、∠AOA 、 ∠ COC
旋转角是___________________________。
演示3
B
A
C
O
B
C
A
旋转角是___________________________。
∠ BOB 、∠AOA 、 ∠ COC
精心做一做
如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
(1)旋转中心是哪一点
(2) 旋转了多少度
(3)如果点G是AB的中点,那么经过上述旋转后,点G到了什么位置
点A
900
A
B
F
C
E
G.
D
.G
(4) 连结EF,那么△AEF是怎样的三角形
本节课我们主要学了什么内容?
旋转的概念:平面内,将一个图形绕着一个定点转动,这样的图形运动称为旋转。
决定旋转的三个要素
旋转中心
旋转方向
旋转角度
通过这节课的学习谈谈你的感想。
同课章节目录
