北师大版数学七年级下册4.3探索三角形全等的条件 课后练习(含答案)
文档属性
| 名称 | 北师大版数学七年级下册4.3探索三角形全等的条件 课后练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 323.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 15:41:31 | ||
图片预览



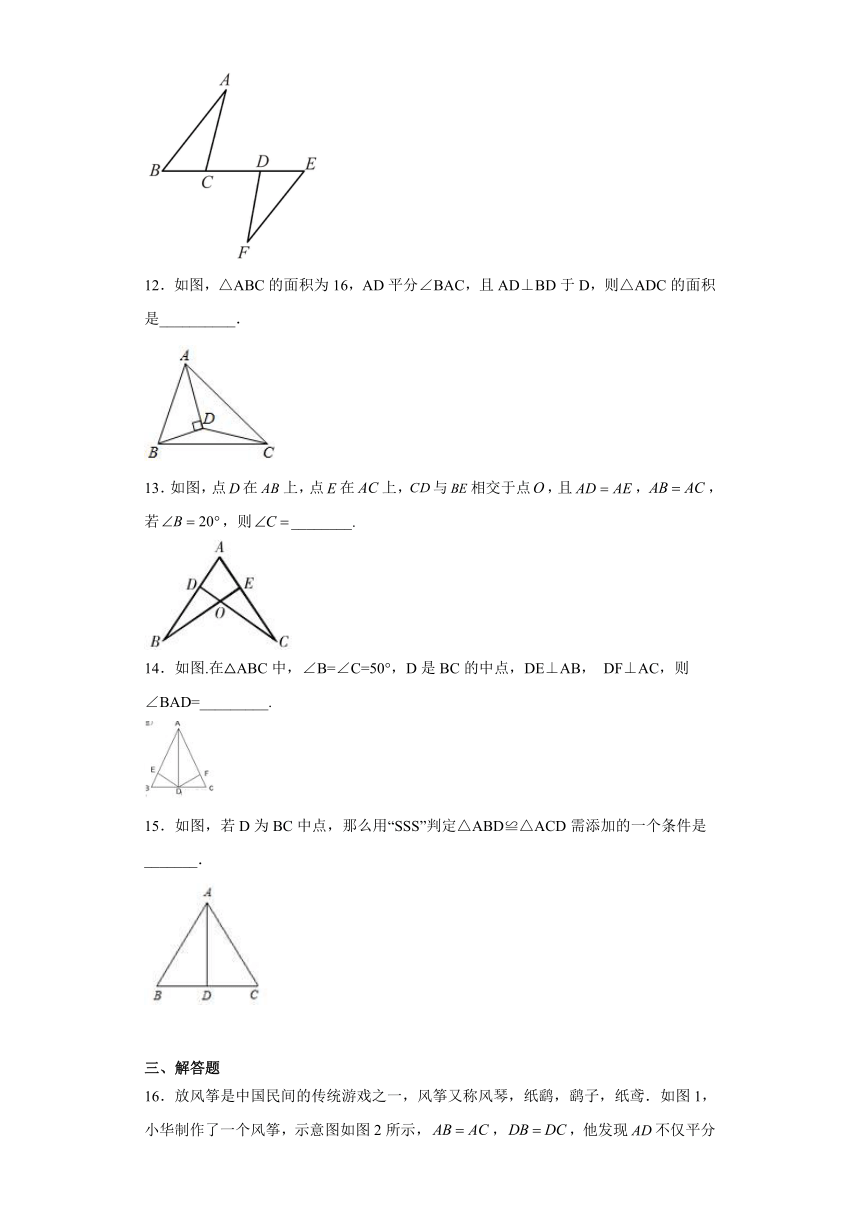

文档简介
4.3 探索三角形全等的条件 课后练习
一、单选题
1.如图,要测量河两岸相对两点,的距离,可以在的垂线上取两点、,使,再作出的垂线,使,,在一条直线上,这时测得的长是,那么的长为( )
A. B. C. D.条件不够,无法判断
2.如图,已知AD∥BC,欲用“边角边”证明△ABC≌△CDA,需补充条件( )
A.AB = CD B.∠B = ∠D C.AD = CB D.∠BAC = ∠DCA
3.如图,小明的三角板损坏了一角,如果他想画一个与该三角板完全重合的三角形,那么他画图的依据是( )
A. B. C. D.
4.如图,已知∠DAB=∠EAC=90°,AD=AB,AE=AC.则下列结论:①BE=CD;②∠ACD=∠AEB;③DC⊥BE;④∠BDC=∠BEC,以上结论正确的共有( )
A.1个 B.2个 C.3个 D.4个
5.如图,∠A=∠D=90°,AC=DB,则ABC≌DCB的依据是( )
A.HL B.ASA C.AAS D.SAS
6.如图,某地需要开辟一条隧道,隧道AB的长度无法直接测量,李师傅设计了一个方案.补充内容不正确的是( )
(1)在地上取一个可以直接到达点A和点B的点C;
(2)连接BC并延长到E,使得 △ ;
(3)连接AC并延长到D,使得 ▽ ;
(4)连接 ○ 并测量出它的长度,即为AB的长;
(5)上述方案的依据是 ◇ .
A.△代表 B.▽代表
C.○代表DE D.◇代表SSS
7.如图,在△ABC中,AB=10,BC=8,AC=6,点O是三条角平分线的交点,则△BOC的BC边上的高是( )
A.1 B.2 C.3 D.4
8.如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则下面添加的条件中错误的是( )
A.△ABC≌△DCB
B.OB=OC,∠A=∠D
C.OB=OC,AB=DC
D.∠A=∠D,∠ABC=∠DCB
9.如图,在和中,点、、、在同一直线上,以下四个论断:①;②;③;④.从中选取哪三个作为条件不能证明和全等的是( )
A.①②③ B.②③④ C.①②④ D.①③④
10.如图,中,,、是边的中线,有;垂足为点E交于点D.且平分交于N.交于H.连接.则下列结论:
①;②;③;④;错误的有( )个.
A.0 B.1 C.3 D.4
二、填空题
11.如图,在和中,,,当添加条件______时,就可得到.(只需填写一个即可)
12.如图,△ABC的面积为16,AD平分∠BAC,且AD⊥BD于D,则△ADC的面积是__________.
13.如图,点在上,点在上,与相交于点,且,,若,则________.
14.如图.在△ABC中,∠B=∠C=50°,D是BC的中点,DE⊥AB, DF⊥AC,则∠BAD=_________.
15.如图,若D为BC中点,那么用“SSS”判定△ABD≌△ACD需添加的一个条件是 _______.
三、解答题
16.放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,,,他发现不仅平分,且平分,你觉得他的发现正确吗?请说明理由.
17.如图,已知,,说明的理由.
18.如图,小明和小华住在同一个小区不同单元楼,他们想要测量小华家所在单元楼的高度.首先他们在两栋单元楼之间选定一点E,然后小明在自己家阳台C处测得E处的俯角为,小华站在E处测得眼睛F到楼端点A的仰角为,发现α与β互余,已知米,米,米.
(1)求证:;
(2)求单元楼的高.
19.写出下列命题的已知、求证,并完成证明过程.
命题:如果一个三角形的两条边相等,那么两条边所对的角也相等(简称:“等边对等角”.)
已知: .
求证: .
证明:
20.如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
参考答案
1.B
2.C
3.B
4.C
5.A
6.D
7.B
8.C
9.A
10.A
11.答案不唯一(如或)
12.
13.
14.40°
15.AB=AC
16解:他的发现正确,理由如下:
在与中,
,
∴,
∴,,
∴不仅平分,且平分.
17.解:∵AD=BC,AE=BE,
∴CE=DE,
在△ACE和△BDE中,
,
∴△ACE≌△BDE(SAS),
∴AC=BD.
18.(1)解:过F作于G,如图:
∴,
∴四边形是矩形,
∴米,米,
∵,
∴,
在与中,
,
∴,
∴;
(2)解:∵,
∴,
∵(米),
∴(米),
∴(米),
答:单元楼的高39米.
19.解:已知:在△ABC中,AB=AC,
求证:∠B=∠C,
证明:过点A作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
∵
∴Rt△ABD≌Rt△ACD(HL),
∴∠B=∠C.
20.相等.
理由是:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
一、单选题
1.如图,要测量河两岸相对两点,的距离,可以在的垂线上取两点、,使,再作出的垂线,使,,在一条直线上,这时测得的长是,那么的长为( )
A. B. C. D.条件不够,无法判断
2.如图,已知AD∥BC,欲用“边角边”证明△ABC≌△CDA,需补充条件( )
A.AB = CD B.∠B = ∠D C.AD = CB D.∠BAC = ∠DCA
3.如图,小明的三角板损坏了一角,如果他想画一个与该三角板完全重合的三角形,那么他画图的依据是( )
A. B. C. D.
4.如图,已知∠DAB=∠EAC=90°,AD=AB,AE=AC.则下列结论:①BE=CD;②∠ACD=∠AEB;③DC⊥BE;④∠BDC=∠BEC,以上结论正确的共有( )
A.1个 B.2个 C.3个 D.4个
5.如图,∠A=∠D=90°,AC=DB,则ABC≌DCB的依据是( )
A.HL B.ASA C.AAS D.SAS
6.如图,某地需要开辟一条隧道,隧道AB的长度无法直接测量,李师傅设计了一个方案.补充内容不正确的是( )
(1)在地上取一个可以直接到达点A和点B的点C;
(2)连接BC并延长到E,使得 △ ;
(3)连接AC并延长到D,使得 ▽ ;
(4)连接 ○ 并测量出它的长度,即为AB的长;
(5)上述方案的依据是 ◇ .
A.△代表 B.▽代表
C.○代表DE D.◇代表SSS
7.如图,在△ABC中,AB=10,BC=8,AC=6,点O是三条角平分线的交点,则△BOC的BC边上的高是( )
A.1 B.2 C.3 D.4
8.如图,在△OBC中,延长BO到D,延长CO到A,要证明OD=OA,则下面添加的条件中错误的是( )
A.△ABC≌△DCB
B.OB=OC,∠A=∠D
C.OB=OC,AB=DC
D.∠A=∠D,∠ABC=∠DCB
9.如图,在和中,点、、、在同一直线上,以下四个论断:①;②;③;④.从中选取哪三个作为条件不能证明和全等的是( )
A.①②③ B.②③④ C.①②④ D.①③④
10.如图,中,,、是边的中线,有;垂足为点E交于点D.且平分交于N.交于H.连接.则下列结论:
①;②;③;④;错误的有( )个.
A.0 B.1 C.3 D.4
二、填空题
11.如图,在和中,,,当添加条件______时,就可得到.(只需填写一个即可)
12.如图,△ABC的面积为16,AD平分∠BAC,且AD⊥BD于D,则△ADC的面积是__________.
13.如图,点在上,点在上,与相交于点,且,,若,则________.
14.如图.在△ABC中,∠B=∠C=50°,D是BC的中点,DE⊥AB, DF⊥AC,则∠BAD=_________.
15.如图,若D为BC中点,那么用“SSS”判定△ABD≌△ACD需添加的一个条件是 _______.
三、解答题
16.放风筝是中国民间的传统游戏之一,风筝又称风琴,纸鹞,鹞子,纸鸢.如图1,小华制作了一个风筝,示意图如图2所示,,,他发现不仅平分,且平分,你觉得他的发现正确吗?请说明理由.
17.如图,已知,,说明的理由.
18.如图,小明和小华住在同一个小区不同单元楼,他们想要测量小华家所在单元楼的高度.首先他们在两栋单元楼之间选定一点E,然后小明在自己家阳台C处测得E处的俯角为,小华站在E处测得眼睛F到楼端点A的仰角为,发现α与β互余,已知米,米,米.
(1)求证:;
(2)求单元楼的高.
19.写出下列命题的已知、求证,并完成证明过程.
命题:如果一个三角形的两条边相等,那么两条边所对的角也相等(简称:“等边对等角”.)
已知: .
求证: .
证明:
20.如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
参考答案
1.B
2.C
3.B
4.C
5.A
6.D
7.B
8.C
9.A
10.A
11.答案不唯一(如或)
12.
13.
14.40°
15.AB=AC
16解:他的发现正确,理由如下:
在与中,
,
∴,
∴,,
∴不仅平分,且平分.
17.解:∵AD=BC,AE=BE,
∴CE=DE,
在△ACE和△BDE中,
,
∴△ACE≌△BDE(SAS),
∴AC=BD.
18.(1)解:过F作于G,如图:
∴,
∴四边形是矩形,
∴米,米,
∵,
∴,
在与中,
,
∴,
∴;
(2)解:∵,
∴,
∵(米),
∴(米),
∴(米),
答:单元楼的高39米.
19.解:已知:在△ABC中,AB=AC,
求证:∠B=∠C,
证明:过点A作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中,
∵
∴Rt△ABD≌Rt△ACD(HL),
∴∠B=∠C.
20.相等.
理由是:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
