空间几何体的结构(浙江省台州市三门县)
文档属性
| 名称 | 空间几何体的结构(浙江省台州市三门县) |  | |
| 格式 | rar | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-12 23:22:00 | ||
图片预览








文档简介
课件42张PPT。空间几何体的结构
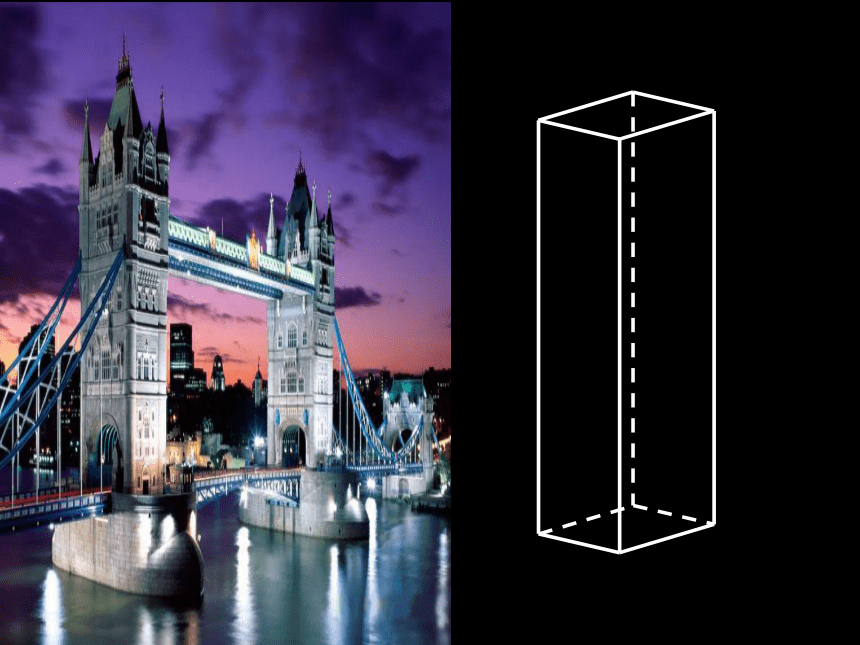
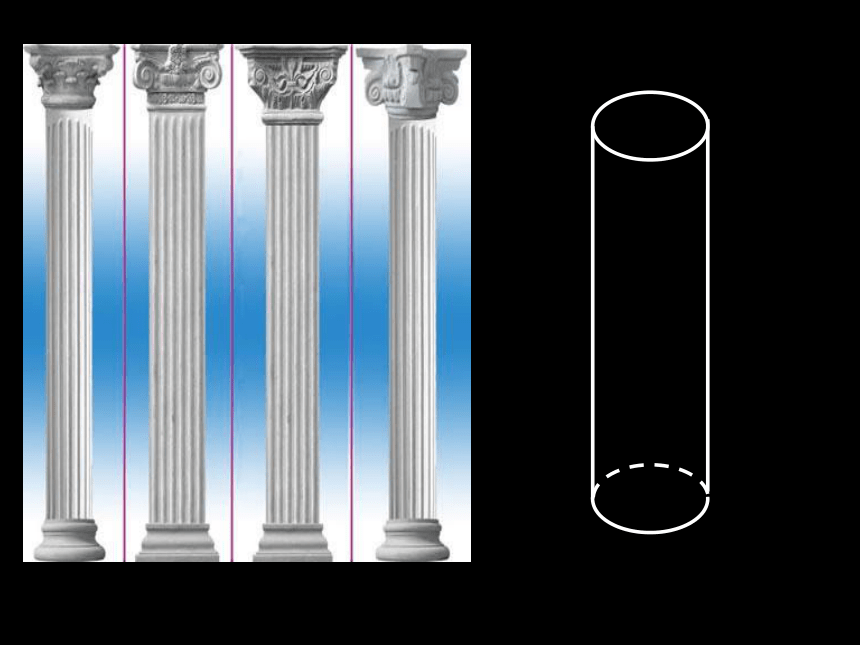
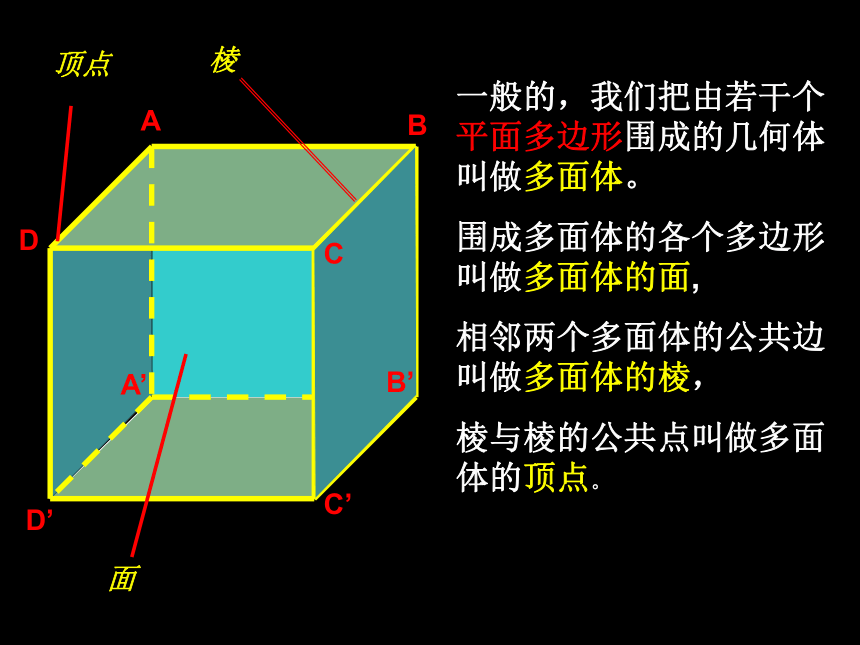
(一)一:空间几何体:对于空间的物体,如果只考虑它的的形状、大小和位置,而不考虑物体的其他性质,从中抽象出来的空间图形叫做空间几何体 观察右边的图片,这些物体具有什么特征?可以怎样对它们进行分类?共同特征:组成几何体的每个面都是平面图形,并且都是平面多边形.共同特征:组成几何体的面不全是平面图形.一般的,我们把由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面,
相邻两个多面体的公共边叫做多面体的棱,
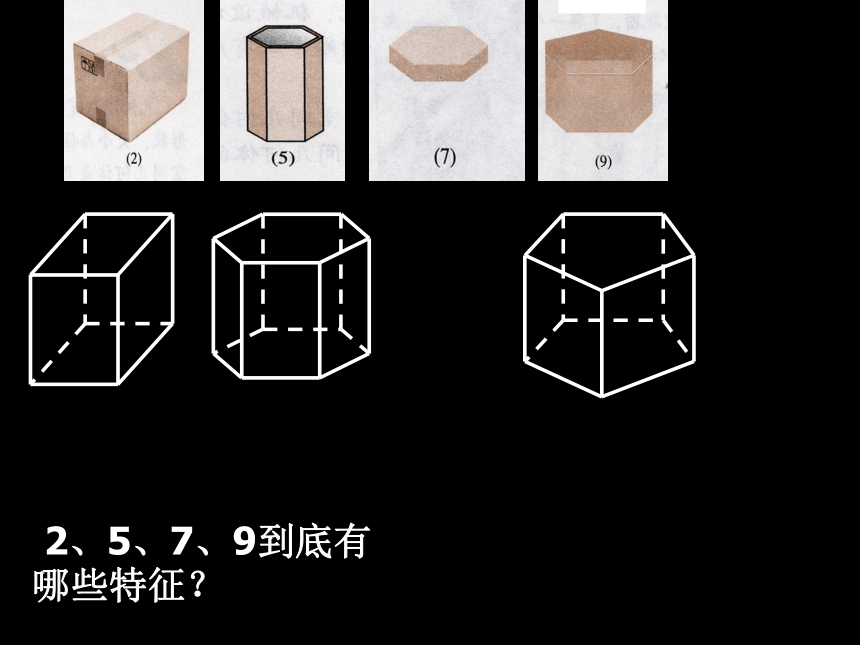
棱与棱的公共点叫做多面体的顶点。ABCDA’B’C’D’ 2、5、7、9到底有
哪些特征? 通过观察有以下特征:
1、有两个面互相平行,
2、其余各面都是四边形,
3、每相邻两个四边形的公共边
都互相平行。 我们把满足上面三个条件的
几何体称为棱柱(prism)。
1、两个互相平行的面叫棱柱的底面。
2、其余各面叫棱柱的侧面。
3、相邻侧面的公共边叫侧棱。
4、侧面与底面的公共顶点叫
棱柱的顶点。
底面是三角形、四边形、五边形…
的棱柱分别叫三棱柱 、四棱柱、五棱
柱…
棱柱的表示法:
四棱柱 ABCD-A’B’C’D’底面侧棱侧面顶点一个长方体,能作为棱柱底面的有几对?探究一个长方体,能作为棱柱底面的有几对?探究一个长方体,能作为棱柱底面的有几对?探究一个长方体,能作为棱柱底面的有几对?探究长方体按如图截去一角后所得的两部分还是棱柱吗?探究A’B’C’D’ABCD长方体按如图截去一角后所得的两部分还是棱柱吗?探究ABCDA’B’C’D’EFGHF’E’H’G’ 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?探究 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?探究 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?探究 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?探究 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?答案: 4对平行平面,只有一对能作为底面.探究 有两个面互相平行,其余各面都是平行四边形
的几何体是棱柱吗?探究定义:
1、有两个面互相平行,
2、其余各面都是四边形,
3、每相邻两个四边形的公共边
都互相平行。
探究棱柱的侧棱与底面一定是垂直的吗?定义
1、有两个面互相平行,
2、其余各面都是四边形,
3、每相邻两个四边形的公共边
都互相平行。 有各种各样的棱柱,你能不能把它们分类呢?
以什么为标准为好?问题 2、棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、…… 三棱柱四棱柱五棱柱3、棱柱的表示法(下图) 用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE- A1B1C1D1E1 。1、棱锥的概念 有一个面是多边形,其余各面是有一个公共顶点的三角形, 由这些面所围成的几何体叫做棱锥。这个多边形面叫做棱锥的底面。 有公共顶点的各个三角形叫做棱锥的侧面。 各侧面的公共顶点叫做棱锥的顶点。 相邻侧面的公共边叫做棱锥 的侧棱。2、棱锥的分类:
按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。三、棱台的结构特征BCADSB1A1C1D1 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。1、棱台的概念:用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…3、棱台的表示法:
棱台用表示上、下底面各顶点的字母来表示,如右图,棱台ABCD-A1B1C1D1 。
(一)一:空间几何体:对于空间的物体,如果只考虑它的的形状、大小和位置,而不考虑物体的其他性质,从中抽象出来的空间图形叫做空间几何体 观察右边的图片,这些物体具有什么特征?可以怎样对它们进行分类?共同特征:组成几何体的每个面都是平面图形,并且都是平面多边形.共同特征:组成几何体的面不全是平面图形.一般的,我们把由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面,
相邻两个多面体的公共边叫做多面体的棱,
棱与棱的公共点叫做多面体的顶点。ABCDA’B’C’D’ 2、5、7、9到底有
哪些特征? 通过观察有以下特征:
1、有两个面互相平行,
2、其余各面都是四边形,
3、每相邻两个四边形的公共边
都互相平行。 我们把满足上面三个条件的
几何体称为棱柱(prism)。
1、两个互相平行的面叫棱柱的底面。
2、其余各面叫棱柱的侧面。
3、相邻侧面的公共边叫侧棱。
4、侧面与底面的公共顶点叫
棱柱的顶点。
底面是三角形、四边形、五边形…
的棱柱分别叫三棱柱 、四棱柱、五棱
柱…
棱柱的表示法:
四棱柱 ABCD-A’B’C’D’底面侧棱侧面顶点一个长方体,能作为棱柱底面的有几对?探究一个长方体,能作为棱柱底面的有几对?探究一个长方体,能作为棱柱底面的有几对?探究一个长方体,能作为棱柱底面的有几对?探究长方体按如图截去一角后所得的两部分还是棱柱吗?探究A’B’C’D’ABCD长方体按如图截去一角后所得的两部分还是棱柱吗?探究ABCDA’B’C’D’EFGHF’E’H’G’ 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?探究 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?探究 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?探究 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?探究 螺丝杆头部是个六棱柱外形,它有几对平行平面?
能作为底面的有几对?答案: 4对平行平面,只有一对能作为底面.探究 有两个面互相平行,其余各面都是平行四边形
的几何体是棱柱吗?探究定义:
1、有两个面互相平行,
2、其余各面都是四边形,
3、每相邻两个四边形的公共边
都互相平行。
探究棱柱的侧棱与底面一定是垂直的吗?定义
1、有两个面互相平行,
2、其余各面都是四边形,
3、每相邻两个四边形的公共边
都互相平行。 有各种各样的棱柱,你能不能把它们分类呢?
以什么为标准为好?问题 2、棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、…… 三棱柱四棱柱五棱柱3、棱柱的表示法(下图) 用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE- A1B1C1D1E1 。1、棱锥的概念 有一个面是多边形,其余各面是有一个公共顶点的三角形, 由这些面所围成的几何体叫做棱锥。这个多边形面叫做棱锥的底面。 有公共顶点的各个三角形叫做棱锥的侧面。 各侧面的公共顶点叫做棱锥的顶点。 相邻侧面的公共边叫做棱锥 的侧棱。2、棱锥的分类:
按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。三、棱台的结构特征BCADSB1A1C1D1 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。1、棱台的概念:用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…3、棱台的表示法:
棱台用表示上、下底面各顶点的字母来表示,如右图,棱台ABCD-A1B1C1D1 。
