第四章三角形之三角形全等基础版(含答案) 2022—2023学年北师大版数学七年级下册
文档属性
| 名称 | 第四章三角形之三角形全等基础版(含答案) 2022—2023学年北师大版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 220.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 20:16:02 | ||
图片预览

文档简介
7下数学第四章三角形之三角形全等(基础版)
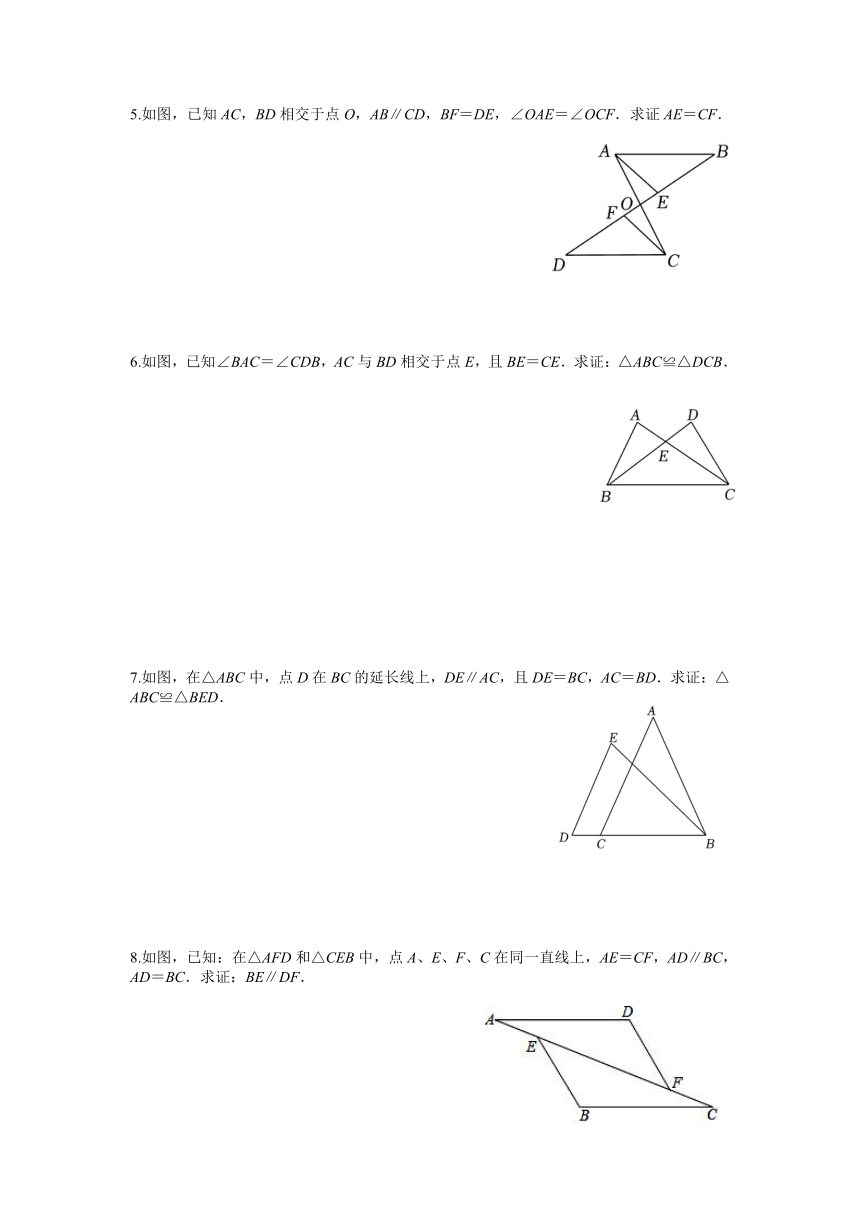
1.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
2.如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE,求证:AE∥CF.
3.如图,点C,F在线段BE上,BF=EC,∠1=∠2,AC=DF.试说明:
(1)△ABC≌△DEF;
(2)AB∥DE.
4.如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点.
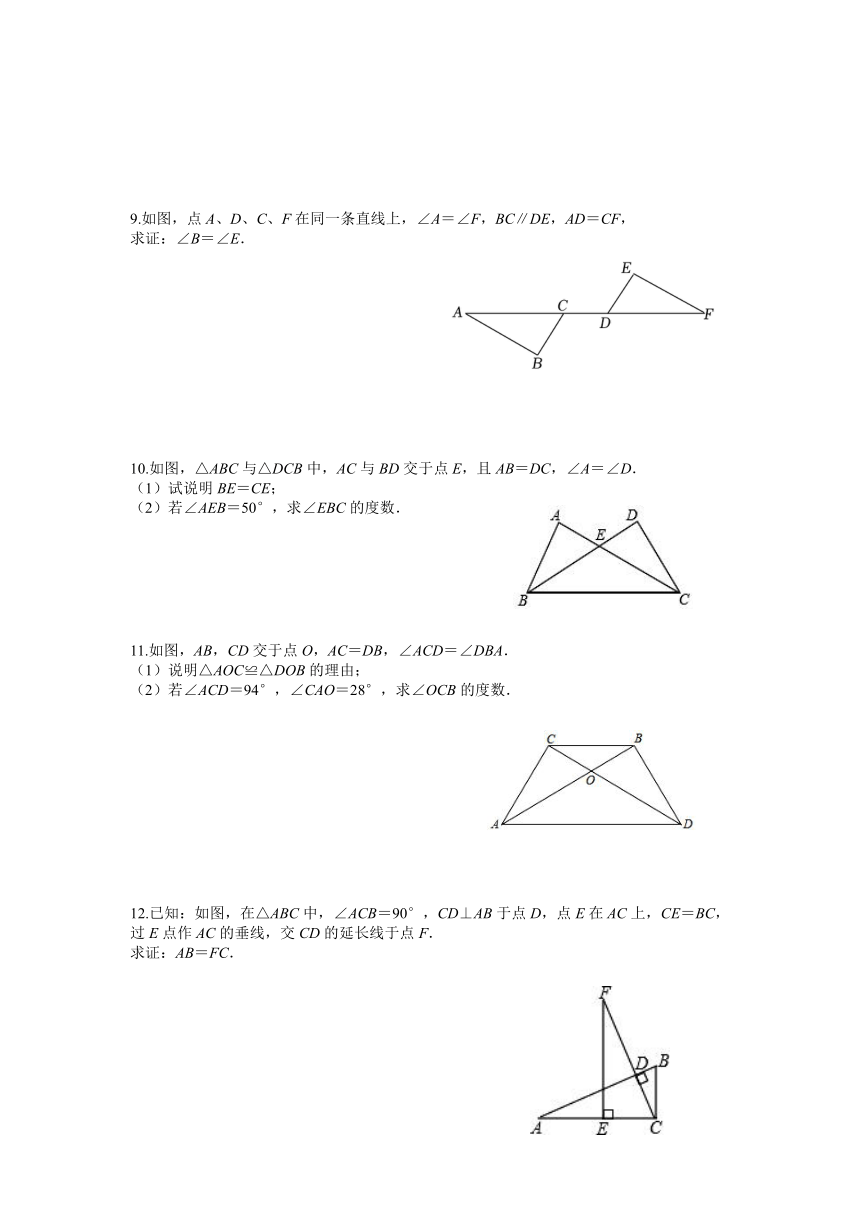
5.如图,已知AC,BD相交于点O,AB∥CD,BF=DE,∠OAE=∠OCF.求证AE=CF.
6.如图,已知∠BAC=∠CDB,AC与BD相交于点E,且BE=CE.求证:△ABC≌△DCB.
7.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.
8.如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.
9.如图,点A、D、C、F在同一条直线上,∠A=∠F,BC∥DE,AD=CF,
求证:∠B=∠E.
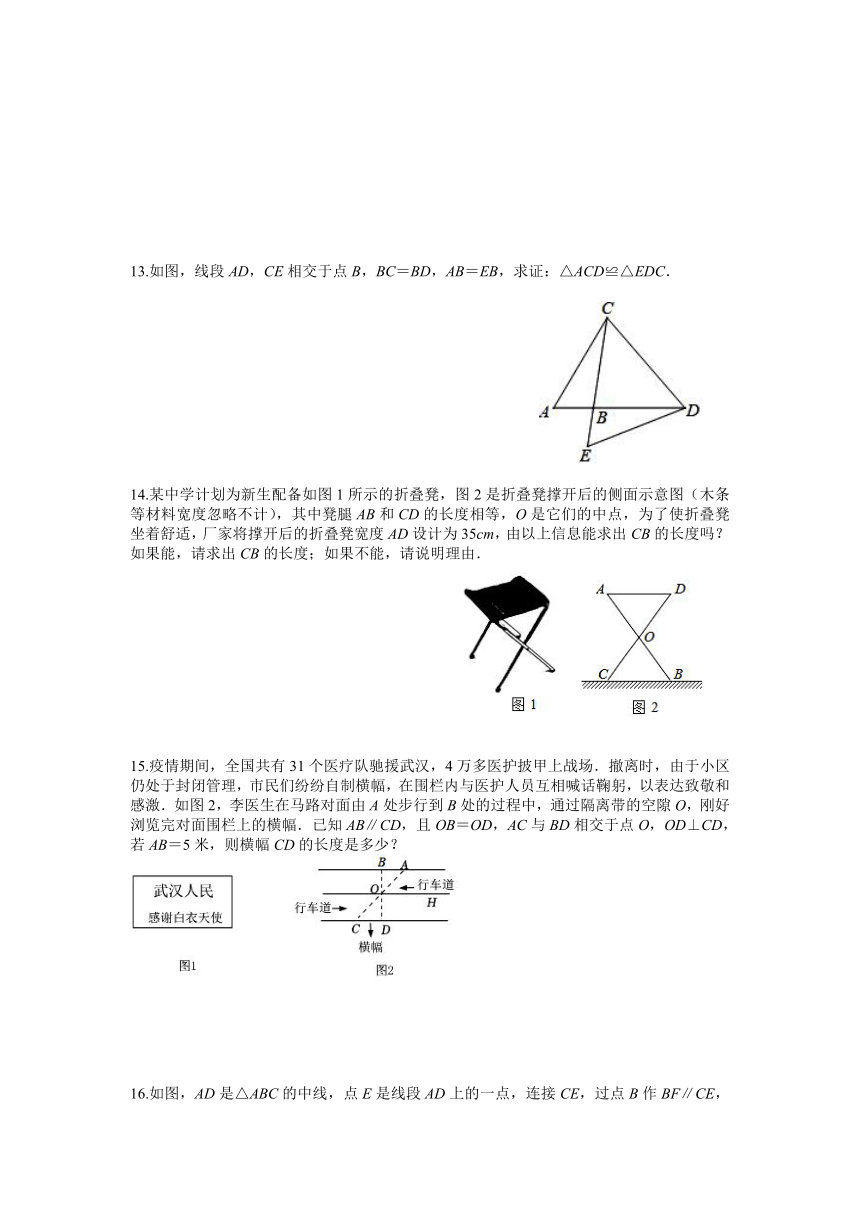
10.如图,△ABC与△DCB中,AC与BD交于点E,且AB=DC,∠A=∠D.
(1)试说明BE=CE;
(2)若∠AEB=50°,求∠EBC的度数.
11.如图,AB,CD交于点O,AC=DB,∠ACD=∠DBA.
(1)说明△AOC≌△DOB的理由;
(2)若∠ACD=94°,∠CAO=28°,求∠OCB的度数.
12.已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.
求证:AB=FC.
13.如图,线段AD,CE相交于点B,BC=BD,AB=EB,求证:△ACD≌△EDC.
14.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
15.疫情期间,全国共有31个医疗队驰援武汉,4万多医护披甲上战场.撤离时,由于小区仍处于封闭管理,市民们纷纷自制横幅,在围栏内与医护人员互相喊话鞠躬,以表达致敬和感激.如图2,李医生在马路对面由A处步行到B处的过程中,通过隔离带的空隙O,刚好浏览完对面围栏上的横幅.已知AB∥CD,且OB=OD,AC与BD相交于点O,OD⊥CD,若AB=5米,则横幅CD的长度是多少?
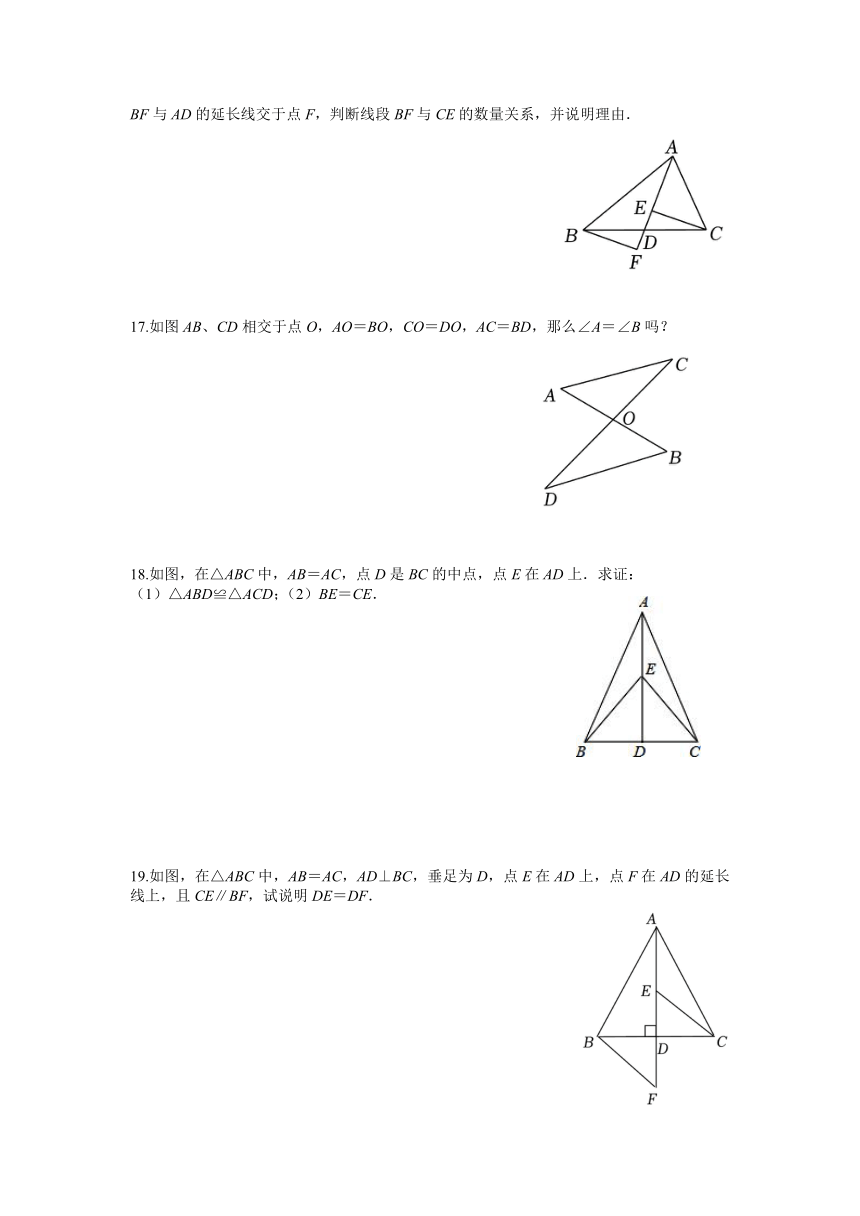
16.如图,AD是△ABC的中线,点E是线段AD上的一点,连接CE,过点B作BF∥CE,BF与AD的延长线交于点F,判断线段BF与CE的数量关系,并说明理由.
17.如图AB、CD相交于点O,AO=BO,CO=DO,AC=BD,那么∠A=∠B吗?
18.如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:
(1)△ABD≌△ACD;(2)BE=CE.
19.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E在AD上,点F在AD的延长线上,且CE∥BF,试说明DE=DF.
如图,点A,B,C,D在一条直线上,且AB=CD,若∠1=∠2,EC=FB.
求证:∠E=∠F.
7下数学第四章三角形之三角形全等(基础版)答案
1.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
【解答】证明:∵FB=CE,
∴FB+FC=CE+FC,
∴BC=EF,
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠DFE,
∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AC=DF.
2.如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE,求证:AE∥CF.
【解答】证明:∵BF=DE,
∴BF+EF=DE+EF,
即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE∥CF.
3.如图,点C,F在线段BE上,BF=EC,∠1=∠2,AC=DF.试说明:
(1)△ABC≌△DEF;
(2)AB∥DE.
【解答】解:(1)∵BF=EC,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS);
(2)∵△ABC≌△DEF,
∴∠B=∠E,
∴AB∥DE.
4.如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点.
【解答】证明:∵AB∥CD,
∴∠A=∠ECD,
在△AEF和△CED中,
,
∴△AEF≌△CED,
∴EF=DE,
∴点E是DF的中点.
5.如图,已知AC,BD相交于点O,AB∥CD,BF=DE,∠OAE=∠OCF.求证AE=CF.
【解答】证明:如图,∵AB∥CD,
∴∠B=∠D,∠BAO=∠DCO,
∵∠OAE=∠OCF,
∴∠BAO﹣∠OAE=∠DCO﹣∠OCF,
∴∠BAE=∠DCF,
∵BF=DE,
∴BF﹣EF=DE﹣EF,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF.
6.如图,已知∠BAC=∠CDB,AC与BD相交于点E,且BE=CE.求证:△ABC≌△DCB.
【解答】证明:∵BE=CE,
∴∠DBC=∠ACB,
在△ABC与△DCB中,
,
∴△ABC≌△DCB(AAS).
7.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.
【解答】证明:∵DE∥AC,
∴∠D=∠ACB,
在△ABC和△BED中,
,
∴△ABC≌△BED(SAS).
8.如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.
【解答】证明:∵AD∥BC,
∴∠A=∠C,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=EC,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS),
∴∠AFD=∠BEC,
∴BE∥DF.
9.如图,点A、D、C、F在同一条直线上,∠A=∠F,BC∥DE,AD=CF,
求证:∠B=∠E.
【解答】证明:∵AD=CF,
∴AD﹣CD=CF﹣CD,
∴AC=DF.
∵BC∥DE,
∴∠BCD=∠EDC,
∴180°﹣∠BCD=180°﹣∠EDC,
∴∠ACB=∠FDE,
在△ABC和△FDE中,
,
∴△ABC≌△FDE(SAS),
∴∠B=∠E.
10.如图,△ABC与△DCB中,AC与BD交于点E,且AB=DC,∠A=∠D.
(1)试说明BE=CE;
(2)若∠AEB=50°,求∠EBC的度数.
【解答】(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴BE=CE;
(2)解:由(1)知,BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
11.如图,AB,CD交于点O,AC=DB,∠ACD=∠DBA.
(1)说明△AOC≌△DOB的理由;
(2)若∠ACD=94°,∠CAO=28°,求∠OCB的度数.
【解答】解:(1)在△AOC和△DOB中,
,
∴△AOC≌△DOB(AAS);
(2)∵∠ACD=94°,∠CAO=28°,
∴∠COB=∠ACD+∠CAO=122°,
∵△AOC≌△DOB,
∴OC=OB,
∴∠OCB=(180°﹣122°)÷2=29°.
12.已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.
求证:AB=FC.
【解答】证明:∵FE⊥AC于点E,∠ACB=90°,
∴∠FEC=∠ACB=90°.
∴∠F+∠ECF=90°.
又∵CD⊥AB于点D,
∴∠A+∠ECF=90°.
∴∠A=∠F.
在△ABC和△FCE中,,
∴△ABC≌△FCE(AAS),
∴AB=FC.
13.如图,线段AD,CE相交于点B,BC=BD,AB=EB,求证:△ACD≌△EDC.
【解答】证明:∵BC=BD,
∴∠ADC=∠ECD,
又AB=EB,
∴BC+EB=BD+AB,
即CE=DA.
在△ACD与△EDC中
,
∴△ACD≌△EDC(SAS).
14.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
【解答】解:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=35cm,
∴CB=35(cm),
答:CB的长度为35cm.
15.疫情期间,全国共有31个医疗队驰援武汉,4万多医护披甲上战场.撤离时,由于小区仍处于封闭管理,市民们纷纷自制横幅,在围栏内与医护人员互相喊话鞠躬,以表达致敬和感激.如图2,李医生在马路对面由A处步行到B处的过程中,通过隔离带的空隙O,刚好浏览完对面围栏上的横幅.已知AB∥CD,且OB=OD,AC与BD相交于点O,OD⊥CD,若AB=5米,则横幅CD的长度是多少?
【解答】解:∵AB∥CD,
∴∠ABO=∠CDO,
∵OD⊥CD,
∴∠CDO=90°,
∴∠ABO=90°,即OB⊥AB,
在△ABO与△CDO中,
,
∴△ABO≌△CDO(ASA),
∴CD=AB=5米.
答:横幅CD的长度是5米.
16.如图,AD是△ABC的中线,点E是线段AD上的一点,连接CE,过点B作BF∥CE,BF与AD的延长线交于点F,判断线段BF与CE的数量关系,并说明理由.
【解答】解:BF=CE.
理由如下:
∵AD是△ABC中线,
∴BD=DC,
∵BF∥CE,
∴∠F=∠CED,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(AAS),
∴BF=CE.
17.如图AB、CD相交于点O,AO=BO,CO=DO,AC=BD,那么∠A=∠B吗?
【解答】解:∠A=∠B,理由如下:
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SSS),
∴∠A=∠B.
18.如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:
(1)△ABD≌△ACD;
(2)BE=CE.
【解答】证明:(1)∵D是BC的中点,
∴BD=CD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS);
(2)由(1)知△ABD≌△ACD,
∴∠BAD=∠CAD,即∠BAE=∠CAE,
在△ABE和△ACE中,
∴△ABE≌△ACE (SAS),
∴BE=CE(全等三角形的对应边相等)
19.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E在AD上,点F在AD的延长线上,且CE∥BF,试说明DE=DF.
【解答】证明:∵AB=AC,AD⊥BC,
∴BD=CD,
∵CE∥BF,
∴∠CED=∠BFD,
在△CED和△BFD中,
,
∴△CED≌△BFD(AAS),
∴DE=DF.
20.如图,点A,B,C,D在一条直线上,且AB=CD,若∠1=∠2,EC=FB.求证:∠E=∠F.
【解答】证明:∵∠1+∠DBF=180°,∠2+∠ACE=180°.
又∵∠1=∠2,
∴∠DBF=∠ACE,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=DB,
在△ACE 和△DBF中,
∴△ACE≌△DBF(SAS),∴∠E=∠F.
1.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
2.如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE,求证:AE∥CF.
3.如图,点C,F在线段BE上,BF=EC,∠1=∠2,AC=DF.试说明:
(1)△ABC≌△DEF;
(2)AB∥DE.
4.如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点.
5.如图,已知AC,BD相交于点O,AB∥CD,BF=DE,∠OAE=∠OCF.求证AE=CF.
6.如图,已知∠BAC=∠CDB,AC与BD相交于点E,且BE=CE.求证:△ABC≌△DCB.
7.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.
8.如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.
9.如图,点A、D、C、F在同一条直线上,∠A=∠F,BC∥DE,AD=CF,
求证:∠B=∠E.
10.如图,△ABC与△DCB中,AC与BD交于点E,且AB=DC,∠A=∠D.
(1)试说明BE=CE;
(2)若∠AEB=50°,求∠EBC的度数.
11.如图,AB,CD交于点O,AC=DB,∠ACD=∠DBA.
(1)说明△AOC≌△DOB的理由;
(2)若∠ACD=94°,∠CAO=28°,求∠OCB的度数.
12.已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.
求证:AB=FC.
13.如图,线段AD,CE相交于点B,BC=BD,AB=EB,求证:△ACD≌△EDC.
14.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
15.疫情期间,全国共有31个医疗队驰援武汉,4万多医护披甲上战场.撤离时,由于小区仍处于封闭管理,市民们纷纷自制横幅,在围栏内与医护人员互相喊话鞠躬,以表达致敬和感激.如图2,李医生在马路对面由A处步行到B处的过程中,通过隔离带的空隙O,刚好浏览完对面围栏上的横幅.已知AB∥CD,且OB=OD,AC与BD相交于点O,OD⊥CD,若AB=5米,则横幅CD的长度是多少?
16.如图,AD是△ABC的中线,点E是线段AD上的一点,连接CE,过点B作BF∥CE,BF与AD的延长线交于点F,判断线段BF与CE的数量关系,并说明理由.
17.如图AB、CD相交于点O,AO=BO,CO=DO,AC=BD,那么∠A=∠B吗?
18.如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:
(1)△ABD≌△ACD;(2)BE=CE.
19.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E在AD上,点F在AD的延长线上,且CE∥BF,试说明DE=DF.
如图,点A,B,C,D在一条直线上,且AB=CD,若∠1=∠2,EC=FB.
求证:∠E=∠F.
7下数学第四章三角形之三角形全等(基础版)答案
1.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
【解答】证明:∵FB=CE,
∴FB+FC=CE+FC,
∴BC=EF,
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠DFE,
∵在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴AC=DF.
2.如图,D、E、F、B在一条直线上,AB=CD,∠B=∠D,BF=DE,求证:AE∥CF.
【解答】证明:∵BF=DE,
∴BF+EF=DE+EF,
即BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE∥CF.
3.如图,点C,F在线段BE上,BF=EC,∠1=∠2,AC=DF.试说明:
(1)△ABC≌△DEF;
(2)AB∥DE.
【解答】解:(1)∵BF=EC,
∴BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS);
(2)∵△ABC≌△DEF,
∴∠B=∠E,
∴AB∥DE.
4.如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点.
【解答】证明:∵AB∥CD,
∴∠A=∠ECD,
在△AEF和△CED中,
,
∴△AEF≌△CED,
∴EF=DE,
∴点E是DF的中点.
5.如图,已知AC,BD相交于点O,AB∥CD,BF=DE,∠OAE=∠OCF.求证AE=CF.
【解答】证明:如图,∵AB∥CD,
∴∠B=∠D,∠BAO=∠DCO,
∵∠OAE=∠OCF,
∴∠BAO﹣∠OAE=∠DCO﹣∠OCF,
∴∠BAE=∠DCF,
∵BF=DE,
∴BF﹣EF=DE﹣EF,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF.
6.如图,已知∠BAC=∠CDB,AC与BD相交于点E,且BE=CE.求证:△ABC≌△DCB.
【解答】证明:∵BE=CE,
∴∠DBC=∠ACB,
在△ABC与△DCB中,
,
∴△ABC≌△DCB(AAS).
7.如图,在△ABC中,点D在BC的延长线上,DE∥AC,且DE=BC,AC=BD.求证:△ABC≌△BED.
【解答】证明:∵DE∥AC,
∴∠D=∠ACB,
在△ABC和△BED中,
,
∴△ABC≌△BED(SAS).
8.如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.
【解答】证明:∵AD∥BC,
∴∠A=∠C,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=EC,
在△ADF和△CBE中,
,
∴△ADF≌△CBE(SAS),
∴∠AFD=∠BEC,
∴BE∥DF.
9.如图,点A、D、C、F在同一条直线上,∠A=∠F,BC∥DE,AD=CF,
求证:∠B=∠E.
【解答】证明:∵AD=CF,
∴AD﹣CD=CF﹣CD,
∴AC=DF.
∵BC∥DE,
∴∠BCD=∠EDC,
∴180°﹣∠BCD=180°﹣∠EDC,
∴∠ACB=∠FDE,
在△ABC和△FDE中,
,
∴△ABC≌△FDE(SAS),
∴∠B=∠E.
10.如图,△ABC与△DCB中,AC与BD交于点E,且AB=DC,∠A=∠D.
(1)试说明BE=CE;
(2)若∠AEB=50°,求∠EBC的度数.
【解答】(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴BE=CE;
(2)解:由(1)知,BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
11.如图,AB,CD交于点O,AC=DB,∠ACD=∠DBA.
(1)说明△AOC≌△DOB的理由;
(2)若∠ACD=94°,∠CAO=28°,求∠OCB的度数.
【解答】解:(1)在△AOC和△DOB中,
,
∴△AOC≌△DOB(AAS);
(2)∵∠ACD=94°,∠CAO=28°,
∴∠COB=∠ACD+∠CAO=122°,
∵△AOC≌△DOB,
∴OC=OB,
∴∠OCB=(180°﹣122°)÷2=29°.
12.已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.
求证:AB=FC.
【解答】证明:∵FE⊥AC于点E,∠ACB=90°,
∴∠FEC=∠ACB=90°.
∴∠F+∠ECF=90°.
又∵CD⊥AB于点D,
∴∠A+∠ECF=90°.
∴∠A=∠F.
在△ABC和△FCE中,,
∴△ABC≌△FCE(AAS),
∴AB=FC.
13.如图,线段AD,CE相交于点B,BC=BD,AB=EB,求证:△ACD≌△EDC.
【解答】证明:∵BC=BD,
∴∠ADC=∠ECD,
又AB=EB,
∴BC+EB=BD+AB,
即CE=DA.
在△ACD与△EDC中
,
∴△ACD≌△EDC(SAS).
14.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长度相等,O是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为35cm,由以上信息能求出CB的长度吗?如果能,请求出CB的长度;如果不能,请说明理由.
【解答】解:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=35cm,
∴CB=35(cm),
答:CB的长度为35cm.
15.疫情期间,全国共有31个医疗队驰援武汉,4万多医护披甲上战场.撤离时,由于小区仍处于封闭管理,市民们纷纷自制横幅,在围栏内与医护人员互相喊话鞠躬,以表达致敬和感激.如图2,李医生在马路对面由A处步行到B处的过程中,通过隔离带的空隙O,刚好浏览完对面围栏上的横幅.已知AB∥CD,且OB=OD,AC与BD相交于点O,OD⊥CD,若AB=5米,则横幅CD的长度是多少?
【解答】解:∵AB∥CD,
∴∠ABO=∠CDO,
∵OD⊥CD,
∴∠CDO=90°,
∴∠ABO=90°,即OB⊥AB,
在△ABO与△CDO中,
,
∴△ABO≌△CDO(ASA),
∴CD=AB=5米.
答:横幅CD的长度是5米.
16.如图,AD是△ABC的中线,点E是线段AD上的一点,连接CE,过点B作BF∥CE,BF与AD的延长线交于点F,判断线段BF与CE的数量关系,并说明理由.
【解答】解:BF=CE.
理由如下:
∵AD是△ABC中线,
∴BD=DC,
∵BF∥CE,
∴∠F=∠CED,
在△BDF和△CDE中,
,
∴△BDF≌△CDE(AAS),
∴BF=CE.
17.如图AB、CD相交于点O,AO=BO,CO=DO,AC=BD,那么∠A=∠B吗?
【解答】解:∠A=∠B,理由如下:
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SSS),
∴∠A=∠B.
18.如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.求证:
(1)△ABD≌△ACD;
(2)BE=CE.
【解答】证明:(1)∵D是BC的中点,
∴BD=CD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS);
(2)由(1)知△ABD≌△ACD,
∴∠BAD=∠CAD,即∠BAE=∠CAE,
在△ABE和△ACE中,
∴△ABE≌△ACE (SAS),
∴BE=CE(全等三角形的对应边相等)
19.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E在AD上,点F在AD的延长线上,且CE∥BF,试说明DE=DF.
【解答】证明:∵AB=AC,AD⊥BC,
∴BD=CD,
∵CE∥BF,
∴∠CED=∠BFD,
在△CED和△BFD中,
,
∴△CED≌△BFD(AAS),
∴DE=DF.
20.如图,点A,B,C,D在一条直线上,且AB=CD,若∠1=∠2,EC=FB.求证:∠E=∠F.
【解答】证明:∵∠1+∠DBF=180°,∠2+∠ACE=180°.
又∵∠1=∠2,
∴∠DBF=∠ACE,
∵AB=CD,
∴AB+BC=CD+BC,
即AC=DB,
在△ACE 和△DBF中,
∴△ACE≌△DBF(SAS),∴∠E=∠F.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
