用字母表示数[上学期]

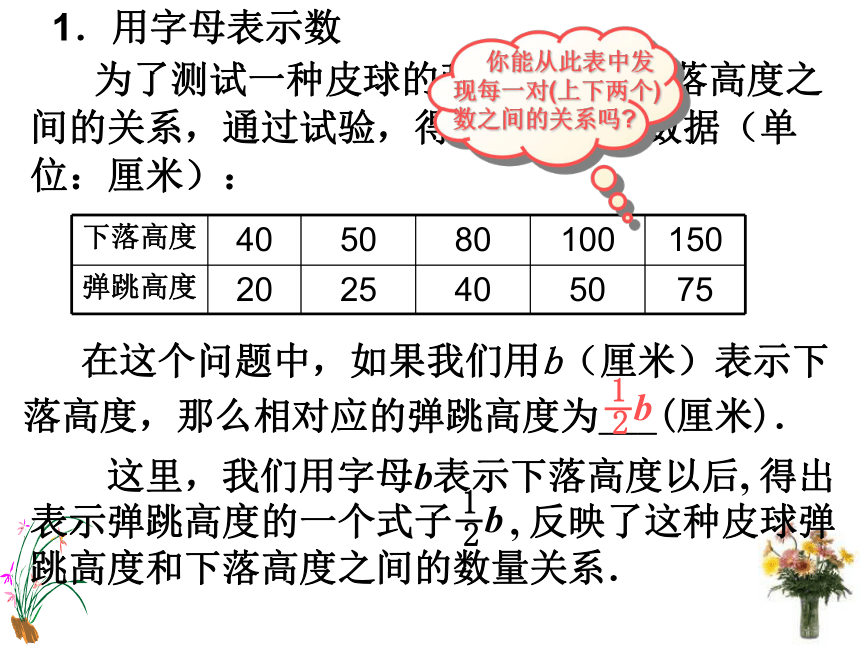
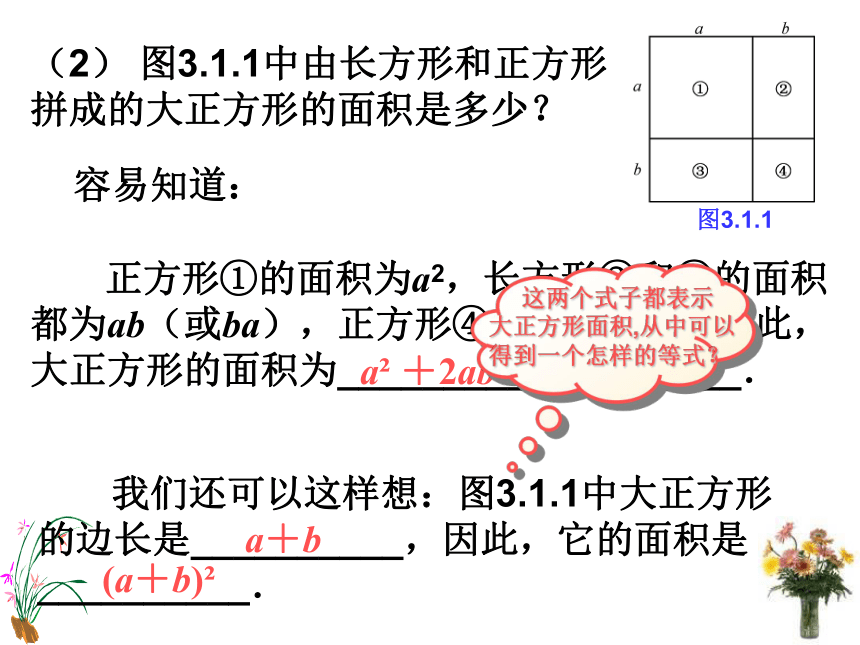
课件13张PPT。第3章 整式的加减§ 3.1 用字母表示数 如图所示的窗框，上半部为半圆，下半部为六个大小一样的长方形，长方形的长与宽的比为3：2。如果长方形的长为0.4米，0.5米，0.6米等等，我们很容易计算出所需的材料的长度。 如果长方形的长是x米，那么所得结果就会是一个x的式子。 将这类式子变形与化简，就会涉及到代数式及整式的有关知识了。本章我们将学习代数式，特别是整式及其加减法。引例回顾1.小学学过哪些几何面积公式？2.请写出路程、速度（平均速度）、时间的关系式。(2)S＝ ab(3)S＝ a2(5)S＝ ?r2(6) s ＝ v t 在这个问题中，如果我们用b（厘米）表示下落高度，那么相对应的弹跳高度为___(厘米)．1．用字母表示数 为了测试一种皮球的弹跳高度与下落高度之间的关系，通过试验，得到下列一组数据（单位：厘米）：让我们再看几个用字母表示数的例子：（1） 如果用a、b表示任意两个有理数，那么加法交换律可以用字母表示为：乘法交换律可以用字母表示为： a＋b＝b＋aab＝ba（2） 图3.1.1中由长方形和正方形拼成的大正方形的面积是多少？ 容易知道： 正方形①的面积为a2，长方形②和③的面积都为ab（或ba），正方形④的面积为b2．因此，大正方形的面积为___________________． 我们还可以这样想：图3.1.1中大正方形的边长是__________，因此，它的面积是__________．图3.1.1a2 ＋2ab＋b2a＋b(a＋b)2（3）我们知道： 这就是说，从1到n这n个正整数的和为_________.1＋2＋3＋4＋5＝________ ＝______,1＋2＋3＋…＋100＝____________ ＝______,… … … … … … … … … … … … …15 5050 从这些例子，我们可以体会到，用字母表示数之后，有些数量之间的关系用含有字母的式子表示，看上去更加简明，更具有普遍意义了． 用字母表示数是代数的一个重要特点,小学里已接触过用字母表示数,初中将进一步研究用字母表示数.例1 填空：
（1）某地为了治理河山，改造环境，计划在第十个五年计划期间植树绿化荒山，如果每年植树绿化x公顷荒山，那么这五年内植树绿化荒山_______公顷；
（2）如果王红用t小时走完的路程为s千米，那么她的速度为_______________千米／时；
（3）每本练习本m元，甲买了5本，乙买了2本，两人一共花了_________________元，甲比乙多花了_________________元．5x(5m＋2m)(5m－2m)元(3)两人共花(5m＋2m)元， 解:甲比乙多花了(5m－2m)元．(1)绿化荒山5x公顷．练习1．填空：
(1)一打铅笔有12枝;n打铅笔有___枝;
(2)三角形的三边分别为3a,4a,5a,则其周长为___；
(3)如图，某广场四角铺上四分之一圆形的草地，若圆形的半径为r米，则共有草地____平方米。2．我们知道：
23＝2×10＋3;类似地，5984＝__×103＋__×102＋__×10＋__. 若某三位数的个位数字为a，十位数字为b，百位数字为c，则此三位数可表示为__________________. 865 ＝8×102 ＋6 ×10 ＋5;c×102＋b×10＋a作业书P92习题3.1第1、2题。