圆周角
图片预览




文档简介
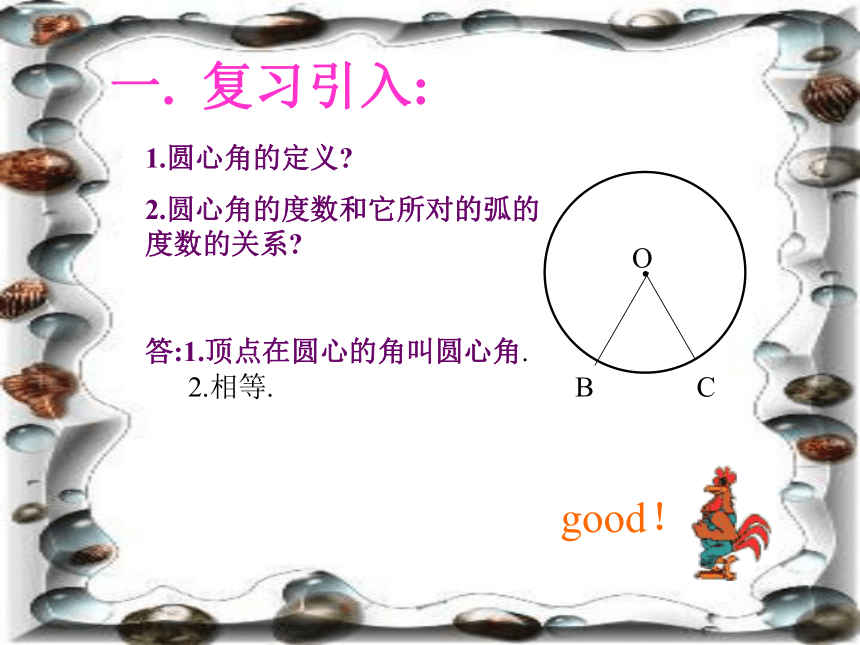
课件21张PPT。圆周角good!一. 复习引入:1.圆心角的定义?
2.圆心角的度数和它所对的弧的 度数的关系?
BC2.相等.答:1.顶点在圆心的角叫圆心角.
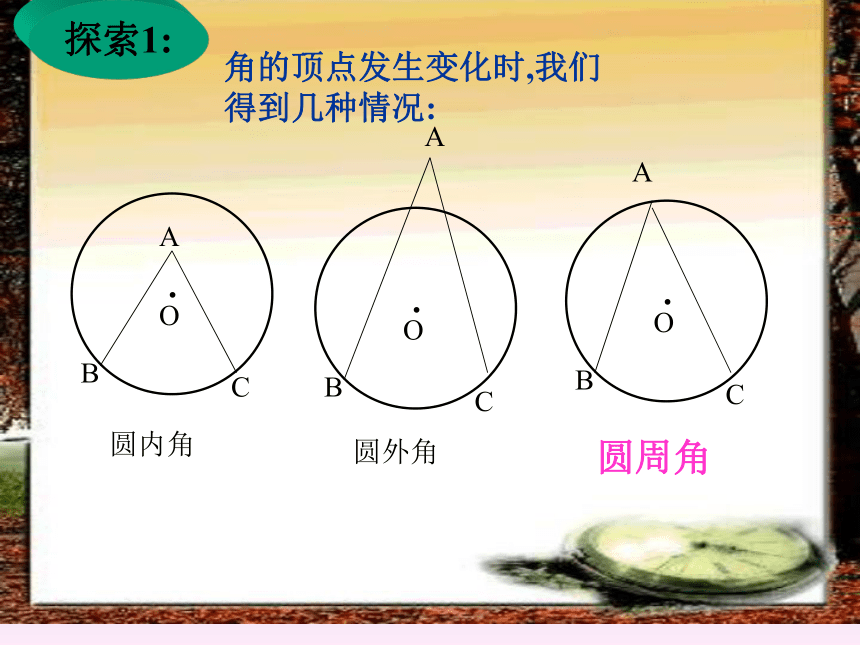
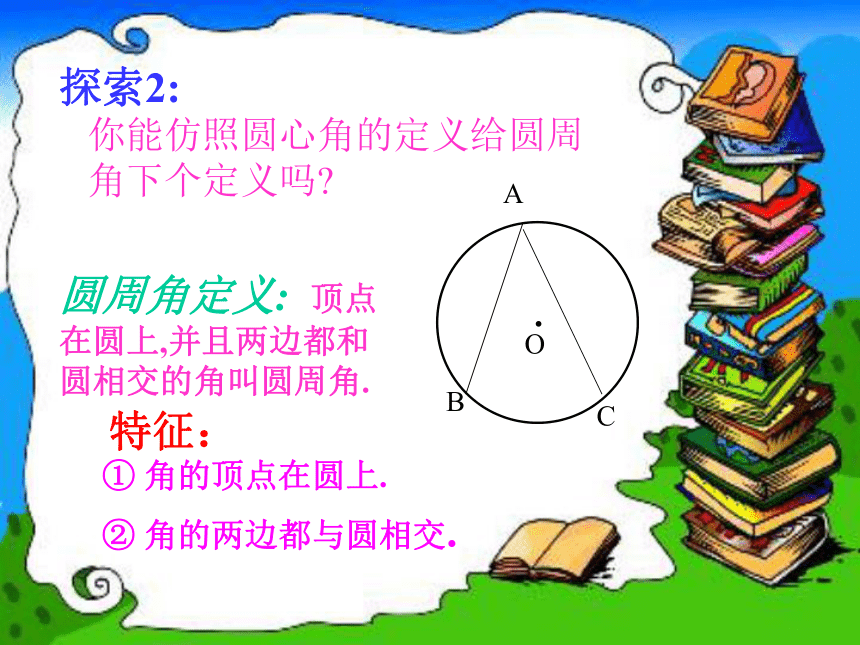
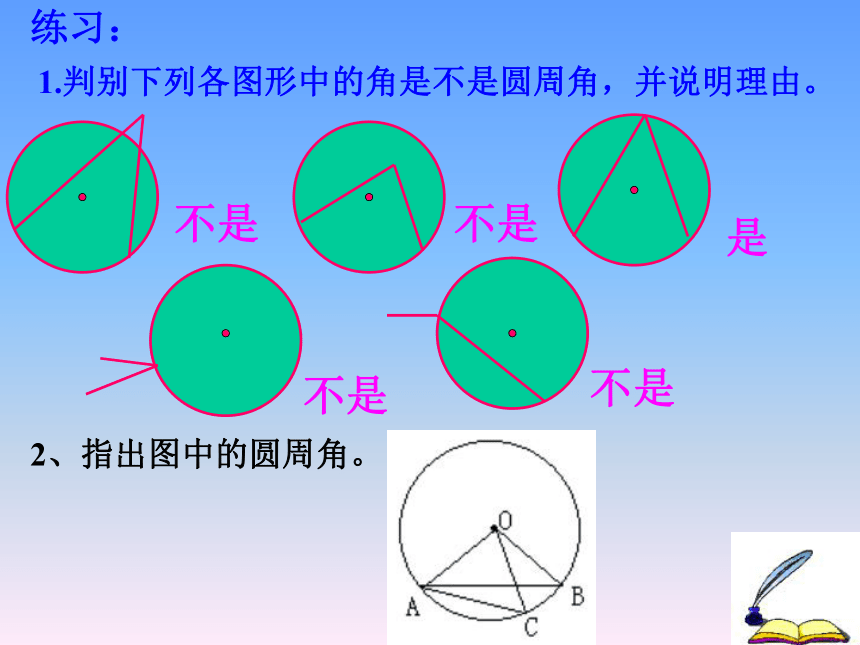
探索1:角的顶点发生变化时,我们得到几种情况:A.OBCAA圆内角圆外角圆周角探索1:探索2:你能仿照圆心角的定义给圆周角下个定义吗?圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:① 角的顶点在圆上.② 角的两边都与圆相交.探究活动:有关圆周角的度数 1. 探究半圆或直径所对的圆周角 等于多少度? 2.90°的圆周角所对的弦是否是直径?线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B), 那 么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢?练习:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是2、指出图中的圆周角。
结论:
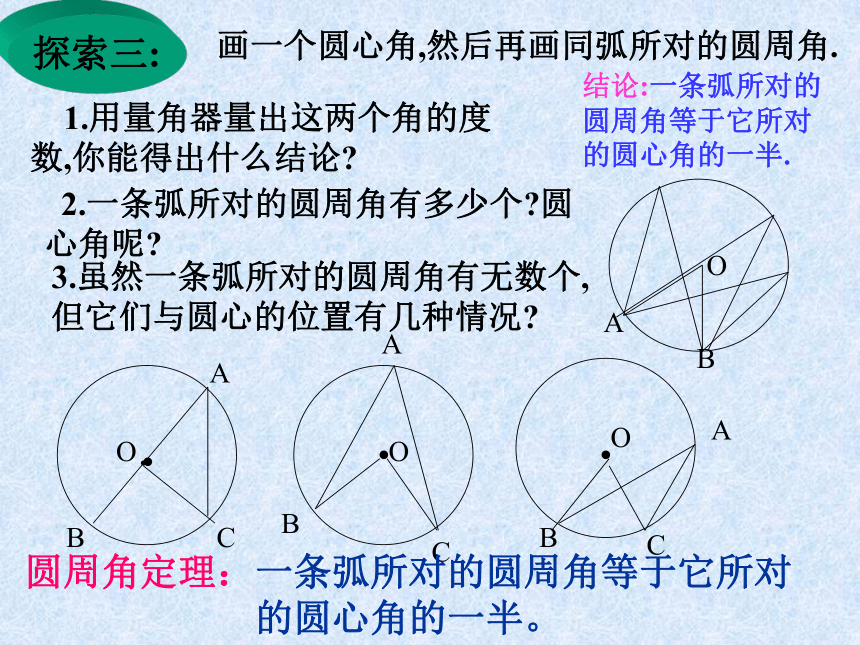
半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径探索三:画一个圆心角,然后再画同弧所对的圆周角.
2.一条弧所对的圆周角有多少个?圆心角呢?3.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置有几种情况? 1.用量角器量出这两个角的度数,你能得出什么结论?结论:一条弧所对的圆周角等于它所对的圆心角的一半.O圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。观察图形、探索圆周角与圆心角的关系定理的证明分三种情况来证明:
(1)圆心在∠BAC的一边上.
OA=OC∠C=∠BAC∠BOC=∠BAC+∠C∠BAC= ∠BOC12(3)圆心在∠BAC的外部.D作直径AD.∠DAB= ∠DOB12∠DAC= ∠DOC12∠DAC-∠DAB= (∠DOC-∠DOB)12∠BAC= ∠BOC12(2)圆心在∠BAC的内部.D作直径AD.∠BAD= ∠BOD12∠DAC= ∠DOC12∠BAD+∠DAC=
(∠BOD+∠DOC)12∠BAC= ∠BOC12在同一圆内,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等.
?
结论:分析定理 因为圆心角的度数等于它所对弧的度数,所以圆周角的度数就等于所对弧度数的一半。巩固练习1.如图,AB是⊙O的直径,∠A=80°,求∠ABC的度数. 练习:2.如图,圆心角∠AOB=100°,则∠ACB=___。1.求圆中角X的度数3、 如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________4、在圆O中,一条弧所对的圆心角和圆周角分别为(2x+100)0和(5x-30)0,则这条弧的度数为____例1.如图:OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.证明:∠ACB= ∠AOB12∠BAC= ∠BOC12∠AOC=2∠BOC∠ACB=2∠BAC分析:1使用曲尺检验工件的凹面,成半圆时为合格.如图所示的三种情况中,哪种是合格的?哪种是不合格的?为什么?
练习: 1、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=350,求∠BOC的度数。 2、如图,在⊙O中,BC=2DE, ∠ BOC=84°,求∠ A的度数。⌒⌒2.如图, ⊙O中,弦AB、CD的延长线交于圆外一点P,∠AOC=100°,求:(1)∠ABC的度数;(2)猜∠P的度数范围,并说明理由.(3)若⊙O中弦AB、CD交于圆内一点P,
∠AOC=100°, ∠ACP的度数范围又如
何呢?总结扩展:这节课主要学习了两个知识点:
1、圆周角定义。
2、圆周角定理及其定理应用。
方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法。
2.圆心角的度数和它所对的弧的 度数的关系?
BC2.相等.答:1.顶点在圆心的角叫圆心角.
探索1:角的顶点发生变化时,我们得到几种情况:A.OBCAA圆内角圆外角圆周角探索1:探索2:你能仿照圆心角的定义给圆周角下个定义吗?圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征:① 角的顶点在圆上.② 角的两边都与圆相交.探究活动:有关圆周角的度数 1. 探究半圆或直径所对的圆周角 等于多少度? 2.90°的圆周角所对的弦是否是直径?线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B), 那 么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?为什么呢?练习:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是2、指出图中的圆周角。
结论:
半圆或直径所对的圆周角都相等,都等于90°(直角)。反过来也是成立的,即90°的圆周角所对的弦是圆的直径探索三:画一个圆心角,然后再画同弧所对的圆周角.
2.一条弧所对的圆周角有多少个?圆心角呢?3.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置有几种情况? 1.用量角器量出这两个角的度数,你能得出什么结论?结论:一条弧所对的圆周角等于它所对的圆心角的一半.O圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。观察图形、探索圆周角与圆心角的关系定理的证明分三种情况来证明:
(1)圆心在∠BAC的一边上.
OA=OC∠C=∠BAC∠BOC=∠BAC+∠C∠BAC= ∠BOC12(3)圆心在∠BAC的外部.D作直径AD.∠DAB= ∠DOB12∠DAC= ∠DOC12∠DAC-∠DAB= (∠DOC-∠DOB)12∠BAC= ∠BOC12(2)圆心在∠BAC的内部.D作直径AD.∠BAD= ∠BOD12∠DAC= ∠DOC12∠BAD+∠DAC=
(∠BOD+∠DOC)12∠BAC= ∠BOC12在同一圆内,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半; 相等的圆周角所对的弧相等.
?
结论:分析定理 因为圆心角的度数等于它所对弧的度数,所以圆周角的度数就等于所对弧度数的一半。巩固练习1.如图,AB是⊙O的直径,∠A=80°,求∠ABC的度数. 练习:2.如图,圆心角∠AOB=100°,则∠ACB=___。1.求圆中角X的度数3、 如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________4、在圆O中,一条弧所对的圆心角和圆周角分别为(2x+100)0和(5x-30)0,则这条弧的度数为____例1.如图:OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.证明:∠ACB= ∠AOB12∠BAC= ∠BOC12∠AOC=2∠BOC∠ACB=2∠BAC分析:1使用曲尺检验工件的凹面,成半圆时为合格.如图所示的三种情况中,哪种是合格的?哪种是不合格的?为什么?
练习: 1、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=350,求∠BOC的度数。 2、如图,在⊙O中,BC=2DE, ∠ BOC=84°,求∠ A的度数。⌒⌒2.如图, ⊙O中,弦AB、CD的延长线交于圆外一点P,∠AOC=100°,求:(1)∠ABC的度数;(2)猜∠P的度数范围,并说明理由.(3)若⊙O中弦AB、CD交于圆内一点P,
∠AOC=100°, ∠ACP的度数范围又如
何呢?总结扩展:这节课主要学习了两个知识点:
1、圆周角定义。
2、圆周角定理及其定理应用。
方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法。
