圆的对称性
图片预览




文档简介
课件18张PPT。圆的对称性做一做,想一想: 一、圆是如何形成的? 1.请同学们画两个等圆,并把其中一个圆剪下,
让两个圆的圆心重合,使得其中一个圆绕着圆心旋转,由此,你发现了什么?2.沿着任意一条直径所在的直线折叠
你所画的任意一个圆. 你又发现了什么?结论:
圆是旋转对称图形,也是中心对称圆形,
而且还是轴对称图形,过圆心的每一条直线
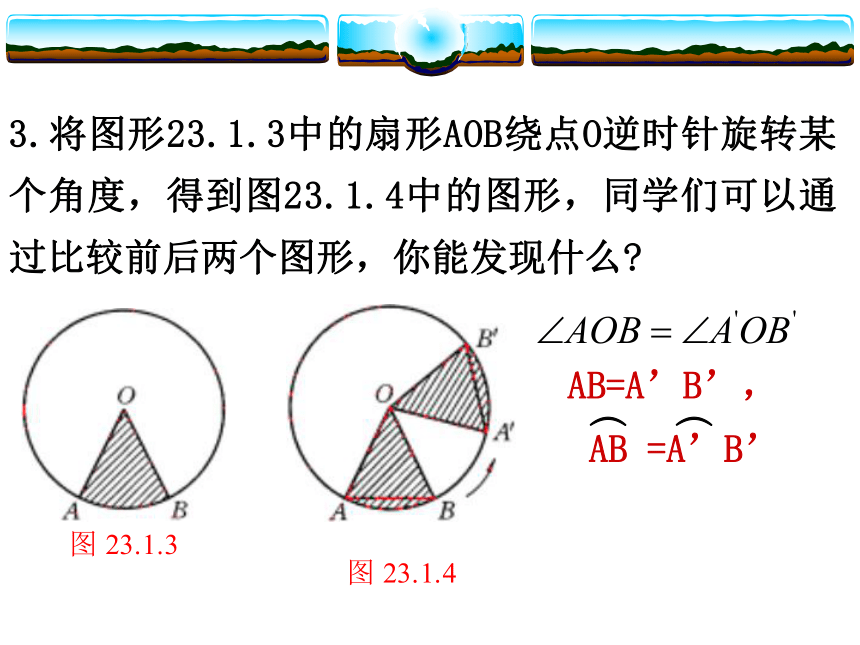
都是圆的对称轴. 3.将图形23.1.3中的扇形AOB绕点O逆时针旋转某个角度,得到图23.1.4中的图形,同学们可以通过比较前后两个图形,你能发现什么? AB=A’B’,实质上, 确定了扇形AOB的大小,所以,
在同一个圆中,如果圆心角相等,
那么它所对的弧相等,所对的弦相等。想一想:
在等圆中,如果圆心角相等,
那么它所对的弧相等吗?所对的弦呢?结论:在同圆或等圆中,如果圆心角相等,那么它所对的弧相等,所对的弦也相等.;在同圆或等圆中,如果弧相等,那么它所对的圆心角
____________,所对的弦_____________;
在同圆或等圆中,如果弦相等,那么它所对的圆心角
____________,所对的弧______________.举一反三:线段AB为直径,.这个以点O为圆心的圆叫作“圆O”,
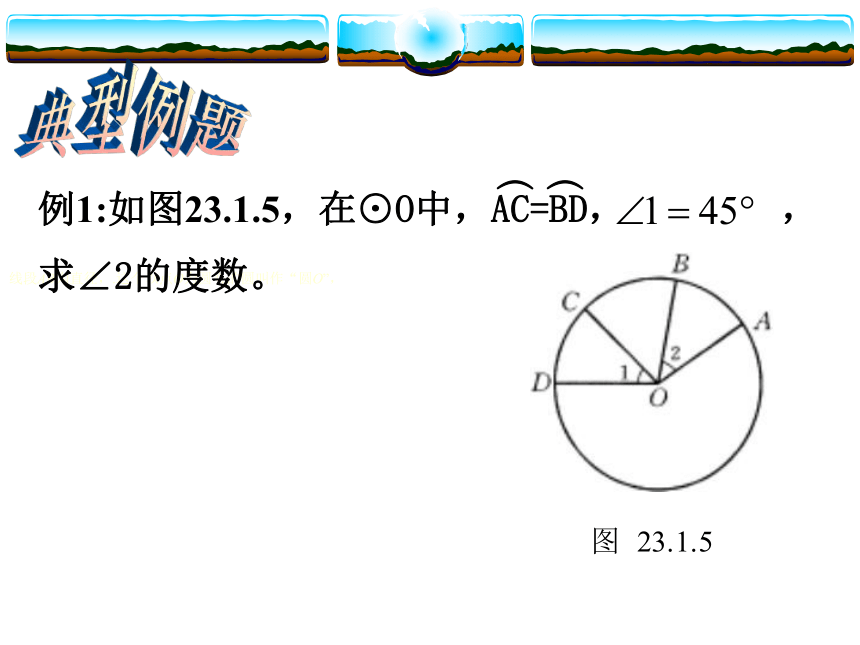
例1:如图23.1.5,在⊙O中,AC=BD, ,
求∠2的度数。
?
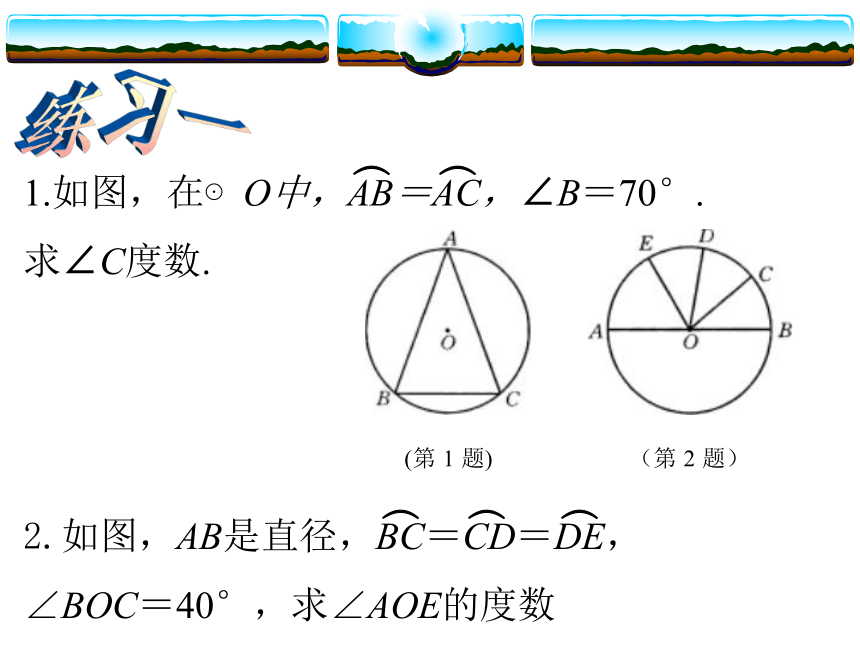
?典型例题︵︵1.如图,在⊙O中,AB=AC,∠B=70°.
求∠C度数.
2.如图,AB是直径,BC=CD=DE,
∠BOC=40°,求∠AOE的度数 练习一︵︵︵︵︵3.如图,在⊙O中,,∠1= ∠2,
试说明:AC= BD
4.如图,已知AD=BC,
试说明AB=CD练习一︵︵ 如图23.1.7,如果在图形纸片上任意画一条
垂直于直径CD的弦AB,垂足为P,再将纸片沿着
直径CD对折,比较AP与PB、AC与CB,
你能发现什么结论?
三、再做一做,想一想: 演示练习二1、如图,AB为⊙O的直径,CD为弦,CD⊥AB于E.则下列结论中错误的是(???? ).
A.∠COE=∠DOE B.CE=DE
C.AE=OE D.BC= BD
︵︵练习二2、如图,⊙O直径CD与弦AB(非直径)交于点M,添加一个条件:____________,
就可得到点M是AB的中点.练习二3、如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.
最大值为____________. 练习二4、如图,矩形ABCD与圆O交于点A、B、E、F,
DE=1cm,EF=3cm,则AB=________cm练习二例2:已知,在⊙O中,弦AB的长为 8 cm ,圆心O到AB的距离为3cm ,
求⊙O的半径。典型例题例3:如图,在圆O中,已知AC=BD,
试说明:(1)OC=OD
(2)AE= BF︵︵典型例题例4:已知⊙O的半径为5cm,弦AB∥CD,
且AB=6cm,CD=8cm,
试求AB与CD之间的距离.课堂小结1、在同圆或等圆中, 对应弧、弦、圆心角之间的关系。
2、垂径定理
如图,在一个半径为6米的圆形花坛里,准备种植六种不同颜色的花卉,要求每种花卉的种植面积相等,请你帮助设计种植方案。思考:
让两个圆的圆心重合,使得其中一个圆绕着圆心旋转,由此,你发现了什么?2.沿着任意一条直径所在的直线折叠
你所画的任意一个圆. 你又发现了什么?结论:
圆是旋转对称图形,也是中心对称圆形,
而且还是轴对称图形,过圆心的每一条直线
都是圆的对称轴. 3.将图形23.1.3中的扇形AOB绕点O逆时针旋转某个角度,得到图23.1.4中的图形,同学们可以通过比较前后两个图形,你能发现什么? AB=A’B’,实质上, 确定了扇形AOB的大小,所以,
在同一个圆中,如果圆心角相等,
那么它所对的弧相等,所对的弦相等。想一想:
在等圆中,如果圆心角相等,
那么它所对的弧相等吗?所对的弦呢?结论:在同圆或等圆中,如果圆心角相等,那么它所对的弧相等,所对的弦也相等.;在同圆或等圆中,如果弧相等,那么它所对的圆心角
____________,所对的弦_____________;
在同圆或等圆中,如果弦相等,那么它所对的圆心角
____________,所对的弧______________.举一反三:线段AB为直径,.这个以点O为圆心的圆叫作“圆O”,
例1:如图23.1.5,在⊙O中,AC=BD, ,
求∠2的度数。
?
?典型例题︵︵1.如图,在⊙O中,AB=AC,∠B=70°.
求∠C度数.
2.如图,AB是直径,BC=CD=DE,
∠BOC=40°,求∠AOE的度数 练习一︵︵︵︵︵3.如图,在⊙O中,,∠1= ∠2,
试说明:AC= BD
4.如图,已知AD=BC,
试说明AB=CD练习一︵︵ 如图23.1.7,如果在图形纸片上任意画一条
垂直于直径CD的弦AB,垂足为P,再将纸片沿着
直径CD对折,比较AP与PB、AC与CB,
你能发现什么结论?
三、再做一做,想一想: 演示练习二1、如图,AB为⊙O的直径,CD为弦,CD⊥AB于E.则下列结论中错误的是(???? ).
A.∠COE=∠DOE B.CE=DE
C.AE=OE D.BC= BD
︵︵练习二2、如图,⊙O直径CD与弦AB(非直径)交于点M,添加一个条件:____________,
就可得到点M是AB的中点.练习二3、如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.
最大值为____________. 练习二4、如图,矩形ABCD与圆O交于点A、B、E、F,
DE=1cm,EF=3cm,则AB=________cm练习二例2:已知,在⊙O中,弦AB的长为 8 cm ,圆心O到AB的距离为3cm ,
求⊙O的半径。典型例题例3:如图,在圆O中,已知AC=BD,
试说明:(1)OC=OD
(2)AE= BF︵︵典型例题例4:已知⊙O的半径为5cm,弦AB∥CD,
且AB=6cm,CD=8cm,
试求AB与CD之间的距离.课堂小结1、在同圆或等圆中, 对应弧、弦、圆心角之间的关系。
2、垂径定理
如图,在一个半径为6米的圆形花坛里,准备种植六种不同颜色的花卉,要求每种花卉的种植面积相等,请你帮助设计种植方案。思考:
