圆的对称性
图片预览



文档简介
(共25张PPT)
圆的对称性
九年级数学上期 华东师大版
1、圆是对称图形吗?它有哪些对称性。
回顾:
圆既是轴对称图形,又是中心对
称图形,也是旋转对称图形。旋转角度
可以是任意度数。
2、能否用手中的圆演示出它的各种对
称性呢?圆的对称轴在哪里,对称中
心和旋转中心在哪里?
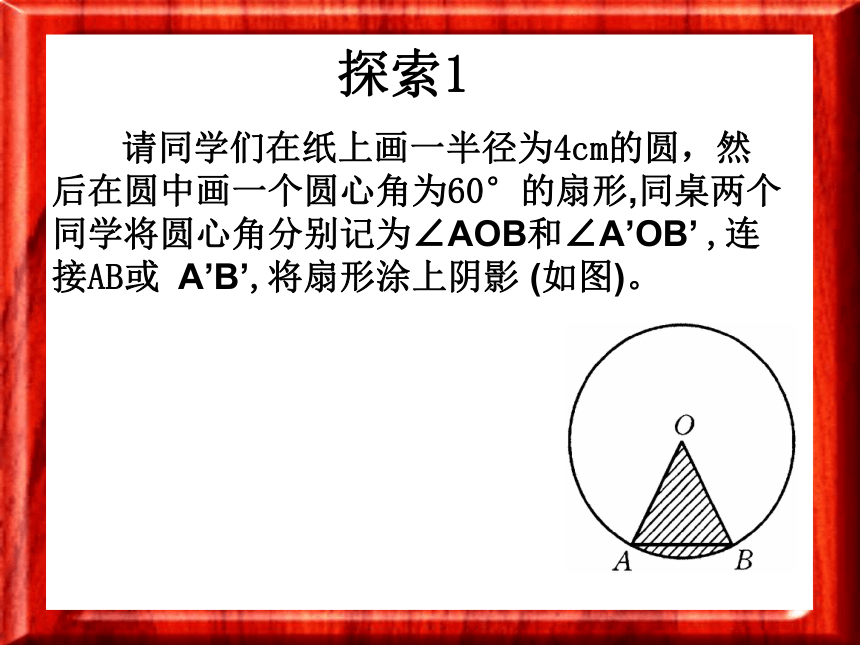
请同学们在纸上画一半径为4cm的圆,然后在圆中画一个圆心角为60°的扇形,同桌两个同学将圆心角分别记为∠AOB和∠A’OB’ ,连接AB或 A’B’,将扇形涂上阴影 (如图)。
探索1
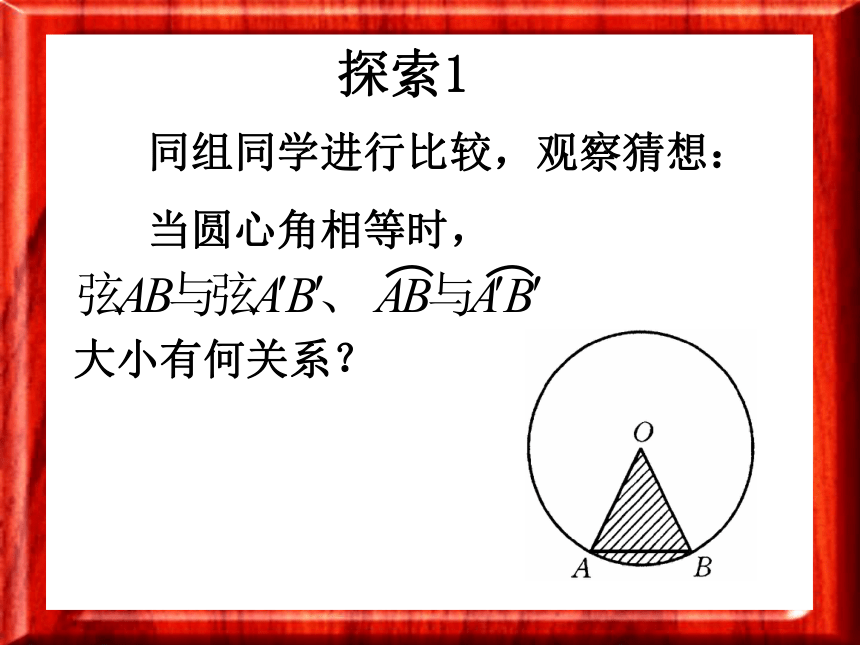
同组同学进行比较,观察猜想:
当圆心角相等时,
探索1
大小有何关系?
将图中的扇形AOB绕点O逆时针旋转某个角度。在得到的图形中,同学们可以通过比较前后两个图形,发现有何关系?
实践操作:
如果
那么
1.在同圆(或等圆)中,相等的圆心角所对的弧相等、所对的弦相等。
结论:
2.在同圆(或等圆)中,如果弦相等,那么所对的圆心角、所对的弧是否相等。
以上三句话如没有在同一圆中,这个结论还会成立吗?
3.在同圆(或等圆) 中,如果弧相等,那么所对的圆心角、所对的弦是否相等。
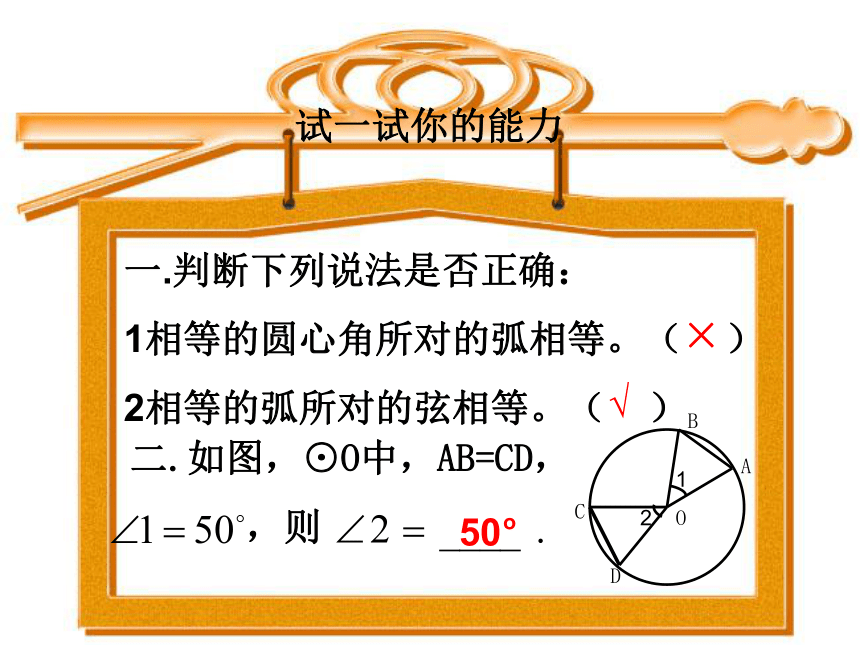
一.判断下列说法是否正确:
1相等的圆心角所对的弧相等。( )
2相等的弧所对的弦相等。( )
二.如图,⊙O中,AB=CD,
,则
O
D
C
A
B
1
2
试一试你的能力
×
√
50
o
如图,在⊙O中,
AC=BD, ,
求∠2的度数。
你会做吗?
解:
∵
AC=BD
(已知)
∴
∴
AB=CD
∴
AC-BC=BD-BC
(等式的性质)
∠1=∠2
(在同圆中,相等的弧所对的圆心角相等)
探究2:
动手操作:
如何将圆两等分?四等分?八等分?
讨论:如何将一个圆3等分? n等分呢?
如图,如果在圆形纸片上任意画一条直径CD,过直径上一点P作弦AB,弦AB与直径CD一定垂直吗?
探究3:
·
1.请同学们将图1沿着直径CD对折,你能发现什么结论?
在⊙O中,如果
2、请同学们将图2沿着直径CD对折,你能发现什么结论?
图1
图2
那么弦
结论:
B
P
O
A
C
D
·
在⊙O中,如果CD是直径
AD=BD,
AC=BC
那么:AP=BP,
垂直于弦的直径
平分这条弦,
并且平分弦所对的两条弧。
1、如图,在⊙O中,弧AB=弧AC,∠B=70°.求∠C 度数.
达标练习:
今天你学到了什么?
1、采用了哪些数学方法?
2、你有什么体会,还有什么疑惑?
3、你认为哪一组的同学表现得最好。
你说我说大家说!
作业
P52习题
A 1、2、3、
B 4、5
学习目标
1、知道圆是中心对称图形和轴对称图形,并能运用其特有的性质推出在同一个圆中,圆心角、弧、弦之间的关系;
2、能运用圆心角、弧、弦之间的关系解决问题,培养善于从实验中获取知识的科学的方法。
3、在积极参与数学活动的过程中,体验发现问题、总结规律的态度以及养成质疑和独立思考的习惯。
2、如图,AB是直径,弧BC=弧CD=弧DE,∠BOC=40°,求∠AOE的度数
讨论:
1.在同圆(或等圆) 中,如果弧相等,那么所对的圆心角、所对的弦是否相等呢?
2.在同圆(或等圆)中,如果弦相等,那么所对的圆心角、所对的弧是否相等呢?
A
B
E
A’
B’
F
O
play
观察:
圆的对称性
九年级数学上期 华东师大版
1、圆是对称图形吗?它有哪些对称性。
回顾:
圆既是轴对称图形,又是中心对
称图形,也是旋转对称图形。旋转角度
可以是任意度数。
2、能否用手中的圆演示出它的各种对
称性呢?圆的对称轴在哪里,对称中
心和旋转中心在哪里?
请同学们在纸上画一半径为4cm的圆,然后在圆中画一个圆心角为60°的扇形,同桌两个同学将圆心角分别记为∠AOB和∠A’OB’ ,连接AB或 A’B’,将扇形涂上阴影 (如图)。
探索1
同组同学进行比较,观察猜想:
当圆心角相等时,
探索1
大小有何关系?
将图中的扇形AOB绕点O逆时针旋转某个角度。在得到的图形中,同学们可以通过比较前后两个图形,发现有何关系?
实践操作:
如果
那么
1.在同圆(或等圆)中,相等的圆心角所对的弧相等、所对的弦相等。
结论:
2.在同圆(或等圆)中,如果弦相等,那么所对的圆心角、所对的弧是否相等。
以上三句话如没有在同一圆中,这个结论还会成立吗?
3.在同圆(或等圆) 中,如果弧相等,那么所对的圆心角、所对的弦是否相等。
一.判断下列说法是否正确:
1相等的圆心角所对的弧相等。( )
2相等的弧所对的弦相等。( )
二.如图,⊙O中,AB=CD,
,则
O
D
C
A
B
1
2
试一试你的能力
×
√
50
o
如图,在⊙O中,
AC=BD, ,
求∠2的度数。
你会做吗?
解:
∵
AC=BD
(已知)
∴
∴
AB=CD
∴
AC-BC=BD-BC
(等式的性质)
∠1=∠2
(在同圆中,相等的弧所对的圆心角相等)
探究2:
动手操作:
如何将圆两等分?四等分?八等分?
讨论:如何将一个圆3等分? n等分呢?
如图,如果在圆形纸片上任意画一条直径CD,过直径上一点P作弦AB,弦AB与直径CD一定垂直吗?
探究3:
·
1.请同学们将图1沿着直径CD对折,你能发现什么结论?
在⊙O中,如果
2、请同学们将图2沿着直径CD对折,你能发现什么结论?
图1
图2
那么弦
结论:
B
P
O
A
C
D
·
在⊙O中,如果CD是直径
AD=BD,
AC=BC
那么:AP=BP,
垂直于弦的直径
平分这条弦,
并且平分弦所对的两条弧。
1、如图,在⊙O中,弧AB=弧AC,∠B=70°.求∠C 度数.
达标练习:
今天你学到了什么?
1、采用了哪些数学方法?
2、你有什么体会,还有什么疑惑?
3、你认为哪一组的同学表现得最好。
你说我说大家说!
作业
P52习题
A 1、2、3、
B 4、5
学习目标
1、知道圆是中心对称图形和轴对称图形,并能运用其特有的性质推出在同一个圆中,圆心角、弧、弦之间的关系;
2、能运用圆心角、弧、弦之间的关系解决问题,培养善于从实验中获取知识的科学的方法。
3、在积极参与数学活动的过程中,体验发现问题、总结规律的态度以及养成质疑和独立思考的习惯。
2、如图,AB是直径,弧BC=弧CD=弧DE,∠BOC=40°,求∠AOE的度数
讨论:
1.在同圆(或等圆) 中,如果弧相等,那么所对的圆心角、所对的弦是否相等呢?
2.在同圆(或等圆)中,如果弦相等,那么所对的圆心角、所对的弧是否相等呢?
A
B
E
A’
B’
F
O
play
观察:
