圆的对称性(垂径定理)
图片预览



文档简介
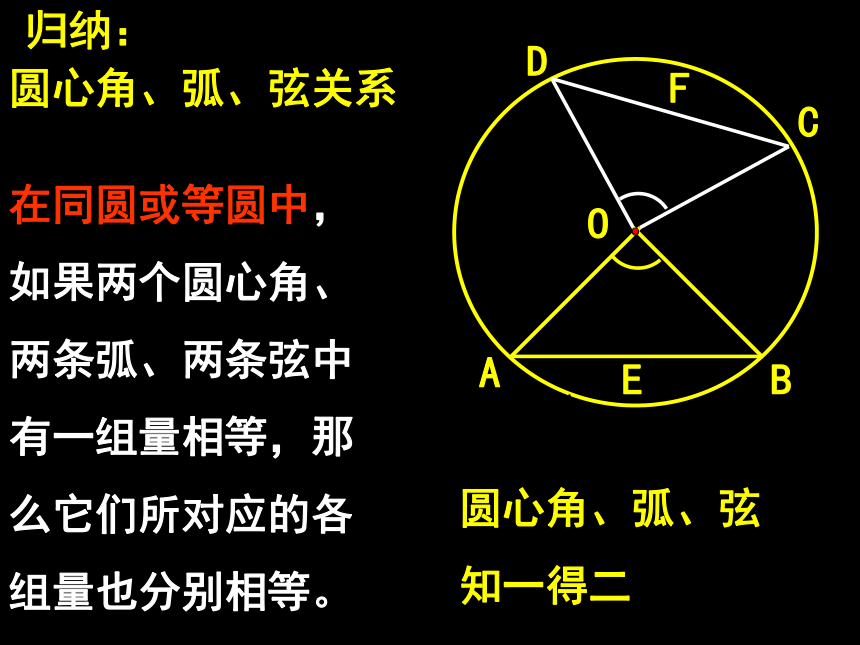
课件23张PPT。垂径定理归纳:OCABA圆心角、弧、弦关系在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的各组量也分别相等。DEF圆心角、弧、弦
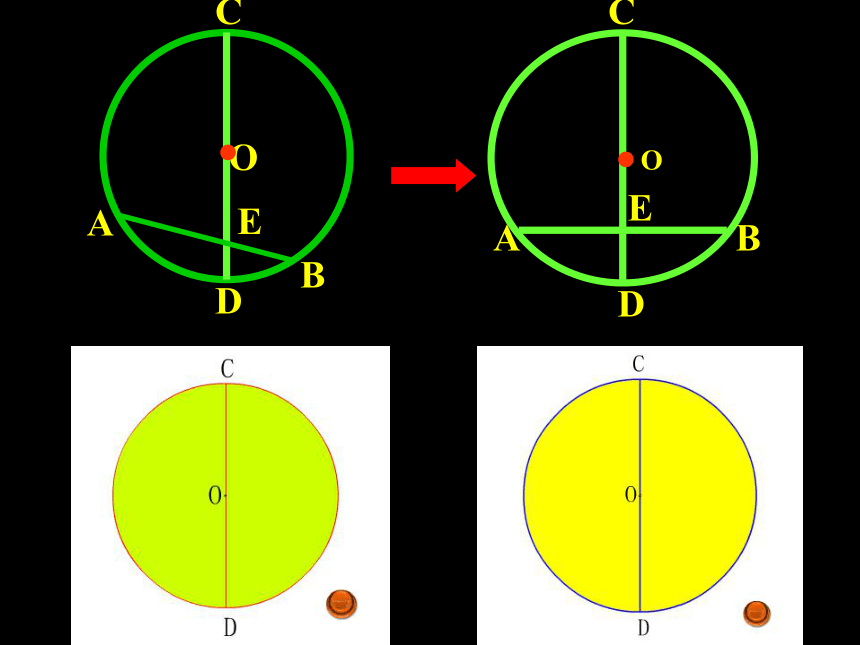
知一得二1、我们所学的圆是不是轴对称图形呢?圆是轴对称图形,经过圆心的每一条直线都是它们的对称轴D{平分弦
平分弦所对的优弧
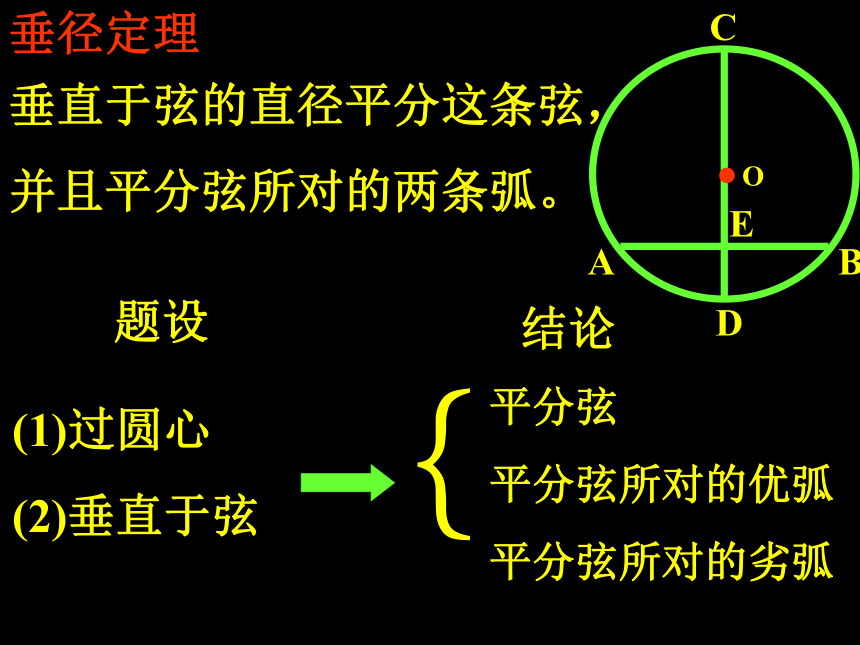
平分弦所对的劣弧垂径定理垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧。题设结论垂直于弦的直径(1)过圆心
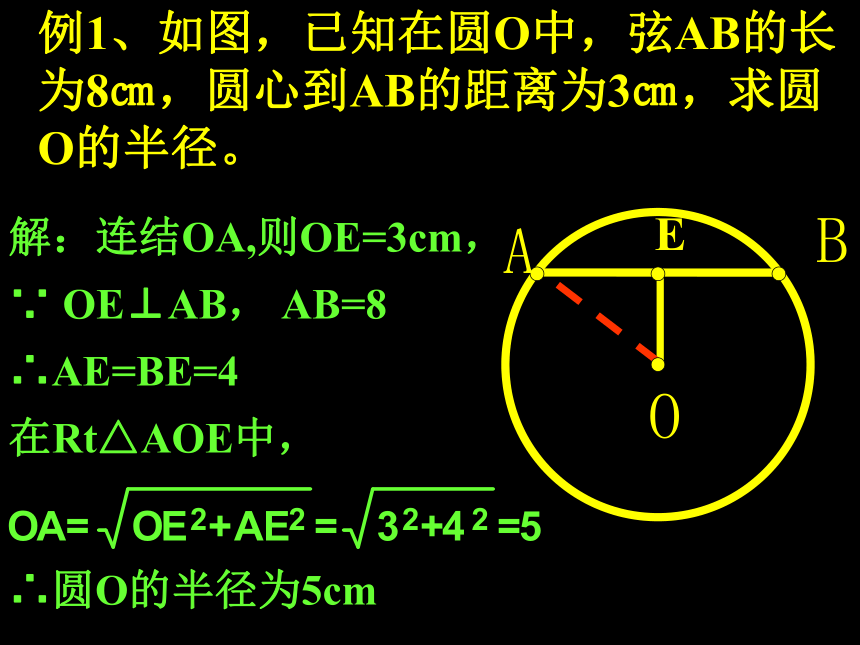
(2)垂直于弦例1、如图,已知在圆O中,弦AB的长为8㎝,圆心到AB的距离为3㎝,求圆O的半径。E解:连结OA,则OE=3cm,
∵ OE⊥AB, AB=8
∴AE=BE=4
在Rt△AOE中,∴圆O的半径为5cmOAB1.(90)【67.5】⊙O的直径为10,圆心O到弦AB的距离为3,则AB的长为_____
2.(93)【63.2】已知⊙O的半径为5㎝,弦AB=8㎝,则圆心O到AB的距离等于 _______㎝.
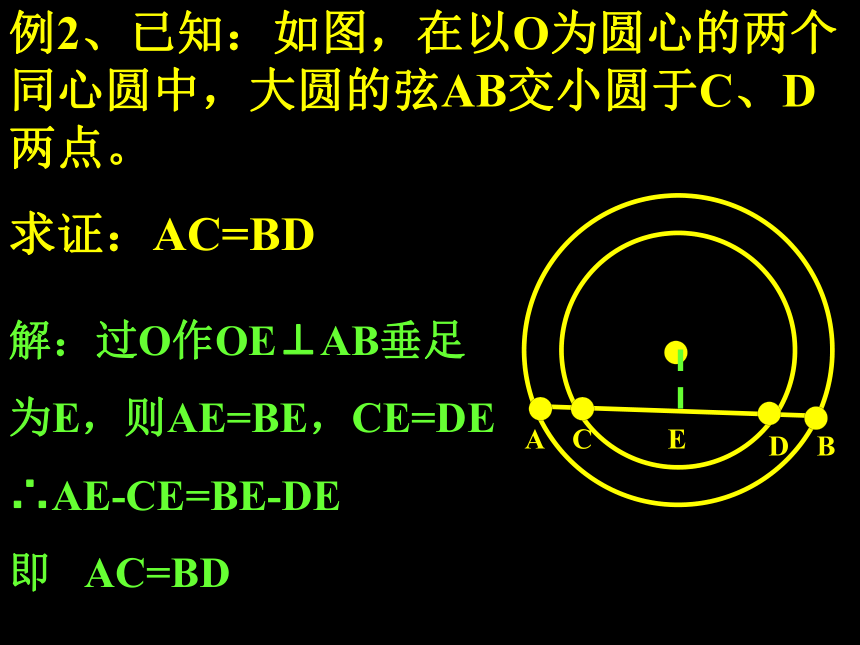
3.(00)【73.1】已知⊙O的半径OA=6cm,弦AB=8cm,则弦心距OD等于______cm 例2、已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
求证:AC=BD解:过O作OE⊥AB垂足为E,则AE=BE,CE=DE
∴AE-CE=BE-DE
即 AC=BDACDBE小结:在圆中,解有关弦的问题时,“垂直于弦的直径”是常用辅助线。垂径定理(二){平分弦
平分弧垂径定理垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧。题设结论(1)过圆心
(2)垂直于弦在⊙o中,
如果AB是⊙o的直径,
AB⊥CD于E
那么CE= ,
= ,
= 。在⊙O中,AB⊥OC于D
那么AD= ,
= 。(1)过圆心 (2)垂直于弦
(3)平分弦 (4)平分弧1、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧(1)过圆心
(3)平分弦 {(2)垂直于弦(4)平分弧(1)过圆心 (2)垂直于弦
(3)平分弦 (4)平分弧(1)过圆心
(4)平分弧 {(2)垂直于弦(4)平分弦2、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧(1)过圆心 (2)垂直于弦
(3)平分弦 (4)平分弧3、弦的垂直平分线经过圆心,并且平分弦所对的两条弧(1)垂直于弦
(3)平分弦 {(1)过圆心 (4)平分弧按图填空:在⊙O中,
(1)若MN⊥AB,MN为直径,
则______,______,______;
(2)若AC=BC,MN为直径,
AB不是直径,则______,______,______;
(3)若MN⊥AB,AC=BC,则_______,________,_____________;
(4)若 ,MN为直径,则________,________,________.AC=BCMN是⊙直径AC=BC例:在半径为20㎜的⊙O中,有长20㎜的弦AB。计算:
(1)点O与AB的距离
(2)∠AOB的度数ACOB如图,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE、∠DOE的度数.1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为
E,如果AB=10,CD=8,求OE.2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为
E,如果BE=2,CD=8,求AB.如图弦AB=10cm,C是 中点,OC交AB于E,求CE=1cm,求⊙O的半径51解直角三角形依据 ??? (1)三边之间的关系:????(2)锐角之间的关系: ? a2+b2=c2(勾股定理) ∠A+∠B=90° (3)边角之间的关系: sinA=cosA =tanA=cotA=
知一得二1、我们所学的圆是不是轴对称图形呢?圆是轴对称图形,经过圆心的每一条直线都是它们的对称轴D{平分弦
平分弦所对的优弧
平分弦所对的劣弧垂径定理垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧。题设结论垂直于弦的直径(1)过圆心
(2)垂直于弦例1、如图,已知在圆O中,弦AB的长为8㎝,圆心到AB的距离为3㎝,求圆O的半径。E解:连结OA,则OE=3cm,
∵ OE⊥AB, AB=8
∴AE=BE=4
在Rt△AOE中,∴圆O的半径为5cmOAB1.(90)【67.5】⊙O的直径为10,圆心O到弦AB的距离为3,则AB的长为_____
2.(93)【63.2】已知⊙O的半径为5㎝,弦AB=8㎝,则圆心O到AB的距离等于 _______㎝.
3.(00)【73.1】已知⊙O的半径OA=6cm,弦AB=8cm,则弦心距OD等于______cm 例2、已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。
求证:AC=BD解:过O作OE⊥AB垂足为E,则AE=BE,CE=DE
∴AE-CE=BE-DE
即 AC=BDACDBE小结:在圆中,解有关弦的问题时,“垂直于弦的直径”是常用辅助线。垂径定理(二){平分弦
平分弧垂径定理垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧。题设结论(1)过圆心
(2)垂直于弦在⊙o中,
如果AB是⊙o的直径,
AB⊥CD于E
那么CE= ,
= ,
= 。在⊙O中,AB⊥OC于D
那么AD= ,
= 。(1)过圆心 (2)垂直于弦
(3)平分弦 (4)平分弧1、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧(1)过圆心
(3)平分弦 {(2)垂直于弦(4)平分弧(1)过圆心 (2)垂直于弦
(3)平分弦 (4)平分弧(1)过圆心
(4)平分弧 {(2)垂直于弦(4)平分弦2、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧(1)过圆心 (2)垂直于弦
(3)平分弦 (4)平分弧3、弦的垂直平分线经过圆心,并且平分弦所对的两条弧(1)垂直于弦
(3)平分弦 {(1)过圆心 (4)平分弧按图填空:在⊙O中,
(1)若MN⊥AB,MN为直径,
则______,______,______;
(2)若AC=BC,MN为直径,
AB不是直径,则______,______,______;
(3)若MN⊥AB,AC=BC,则_______,________,_____________;
(4)若 ,MN为直径,则________,________,________.AC=BCMN是⊙直径AC=BC例:在半径为20㎜的⊙O中,有长20㎜的弦AB。计算:
(1)点O与AB的距离
(2)∠AOB的度数ACOB如图,⊙O的直径AB垂直于弦CD,AB、CD相交于点E,∠COD=100°,求∠COE、∠DOE的度数.1.如图,AB是⊙O的直径,弦CD⊥AB,垂足为
E,如果AB=10,CD=8,求OE.2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为
E,如果BE=2,CD=8,求AB.如图弦AB=10cm,C是 中点,OC交AB于E,求CE=1cm,求⊙O的半径51解直角三角形依据 ??? (1)三边之间的关系:????(2)锐角之间的关系: ? a2+b2=c2(勾股定理) ∠A+∠B=90° (3)边角之间的关系: sinA=cosA =tanA=cotA=
