圆的对称性
图片预览



文档简介
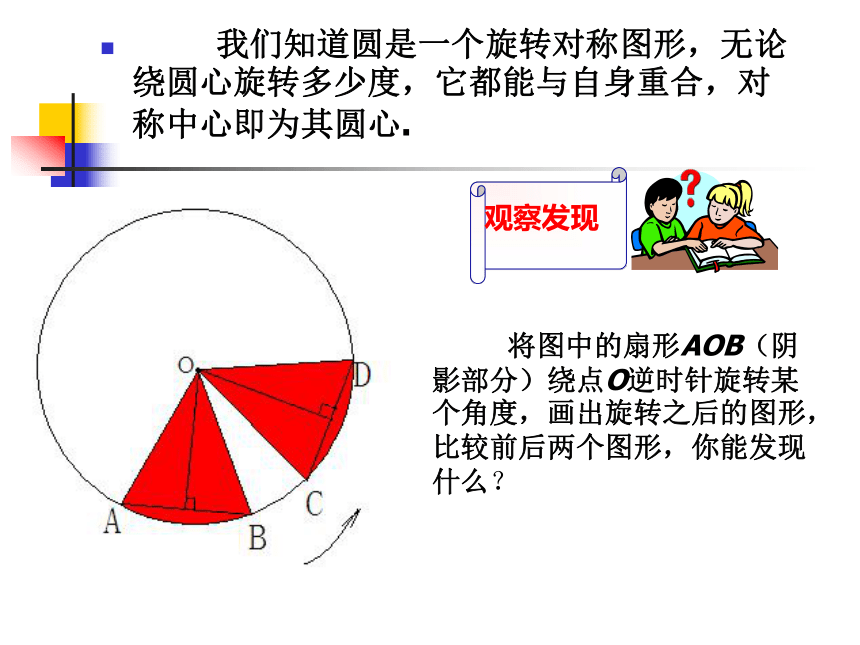
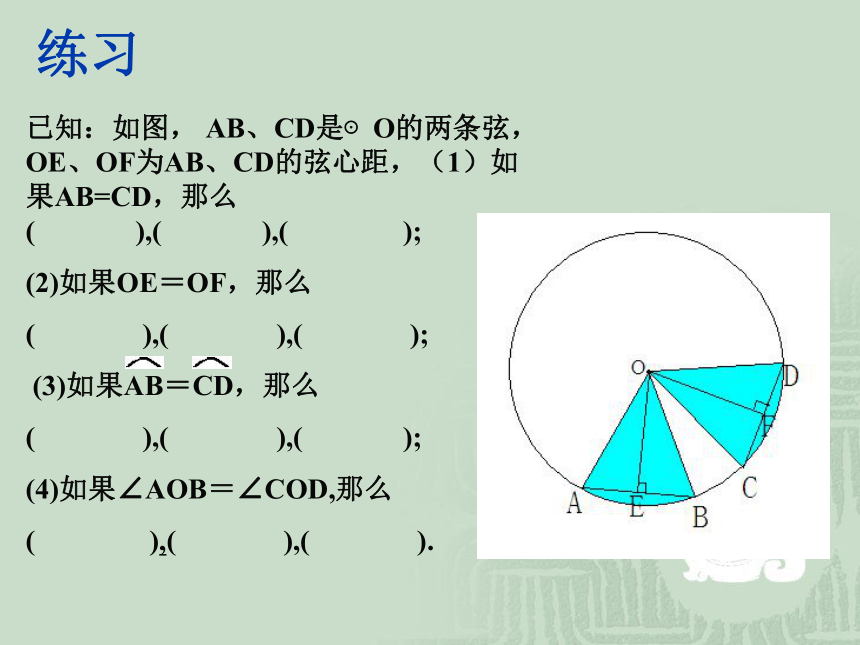
课件16张PPT。圆的对称性 我们知道圆是一个旋转对称图形,无论绕圆心旋转多少度,它都能与自身重合,对称中心即为其圆心. 将图中的扇形AOB(阴影部分)绕点O逆时针旋转某个角度,画出旋转之后的图形,比较前后两个图形,你能发现什么?定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。练习已知:如图, AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,(1)如果AB=CD,那么( ),( ),( );
(2)如果OE=OF,那么
( ),( ),( );
(3)如果AB=CD,那么
( ),( ),( );
(4)如果∠AOB=∠COD,那么
( ),( ),( ).
判断:
1、等弦所对的弧相等。 ( )
2、等弧所对的弦相等。 ( )
3、圆心角相等,所对的弦相等 ( )
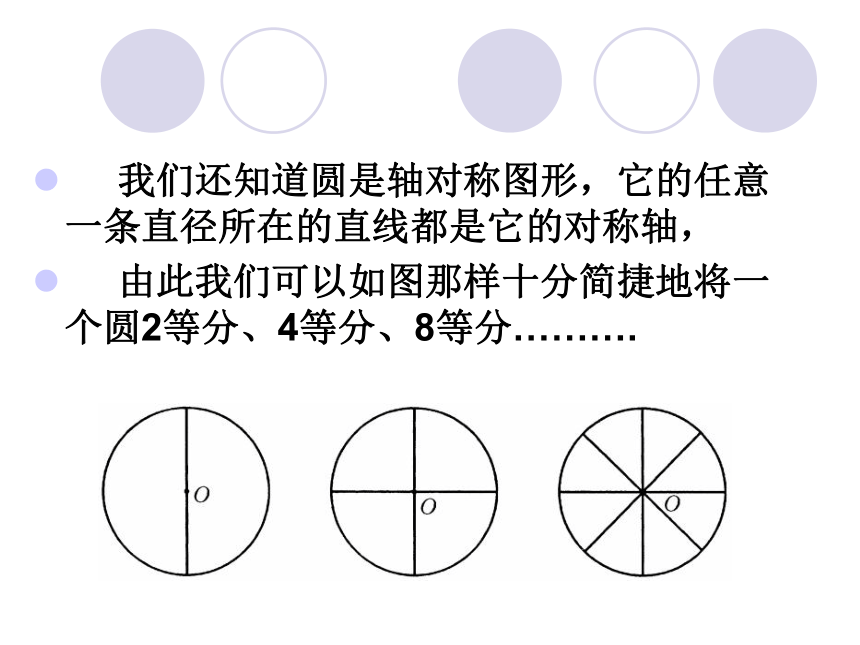
4、弦相等,所对的圆心角相等 ( ) ×××√ 我们还知道圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴,
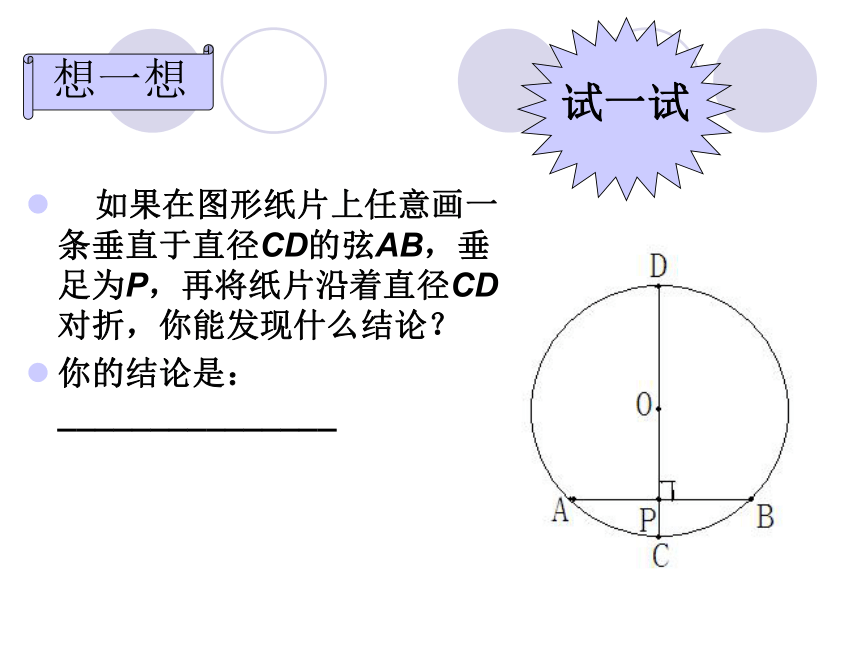
由此我们可以如图那样十分简捷地将一个圆2等分、4等分、8等分……….想一想 如果在图形纸片上任意画一条垂直于直径CD的弦AB,垂足为P,再将纸片沿着直径CD对折,你能发现什么结论?
你的结论是:_______________试一试结论(垂径定理) 垂直于弦的直径平分弦,并且平分这条弦所对的弧. 推论(1)垂直于弦,(2)平分弦(3)平分弧.(4)是直径(过圆心)
只要满足其中的两个条件,其余随之成立.
练习 1.如图,在⊙O中,
AB=AC,∠B=70°
求∠C度数. 2.如图,AB是直径,
BC=CD=DE,
∠BOC=40°,
求∠AOE的度数. 2.如图,AB是直径,
BC=CD=DE,
∠BOC=40°,
求∠AOE的度数.·DOM 如图,点O是∠BPD平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D 求证:AB=CD证明:作OM⊥AB,ON⊥CD,M、N为垂足,PABCN·ABCDOMN变化如果BD=CD那么AB=AC吗?D?ABCDMNO如图M、N为AB、CD的中点,且AB=CD.
求证:∠AMN=∠CNM如图⊙A与⊙B是两个等圆,直线CF∥AB,分别交⊙A于点C、D,交⊙B于点E、F。
求证:∠CAD=∠EBF?A?BCDEFGH?OABCDEF已知AB和CD是⊙O的两条弦,OE和OF分别是AB和CD的弦心距,如果AB>CD,那么OE和OF有什么关系?为什么?想一想?再见
(2)如果OE=OF,那么
( ),( ),( );
(3)如果AB=CD,那么
( ),( ),( );
(4)如果∠AOB=∠COD,那么
( ),( ),( ).
判断:
1、等弦所对的弧相等。 ( )
2、等弧所对的弦相等。 ( )
3、圆心角相等,所对的弦相等 ( )
4、弦相等,所对的圆心角相等 ( ) ×××√ 我们还知道圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴,
由此我们可以如图那样十分简捷地将一个圆2等分、4等分、8等分……….想一想 如果在图形纸片上任意画一条垂直于直径CD的弦AB,垂足为P,再将纸片沿着直径CD对折,你能发现什么结论?
你的结论是:_______________试一试结论(垂径定理) 垂直于弦的直径平分弦,并且平分这条弦所对的弧. 推论(1)垂直于弦,(2)平分弦(3)平分弧.(4)是直径(过圆心)
只要满足其中的两个条件,其余随之成立.
练习 1.如图,在⊙O中,
AB=AC,∠B=70°
求∠C度数. 2.如图,AB是直径,
BC=CD=DE,
∠BOC=40°,
求∠AOE的度数. 2.如图,AB是直径,
BC=CD=DE,
∠BOC=40°,
求∠AOE的度数.·DOM 如图,点O是∠BPD平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D 求证:AB=CD证明:作OM⊥AB,ON⊥CD,M、N为垂足,PABCN·ABCDOMN变化如果BD=CD那么AB=AC吗?D?ABCDMNO如图M、N为AB、CD的中点,且AB=CD.
求证:∠AMN=∠CNM如图⊙A与⊙B是两个等圆,直线CF∥AB,分别交⊙A于点C、D,交⊙B于点E、F。
求证:∠CAD=∠EBF?A?BCDEFGH?OABCDEF已知AB和CD是⊙O的两条弦,OE和OF分别是AB和CD的弦心距,如果AB>CD,那么OE和OF有什么关系?为什么?想一想?再见
