圆周角定理
图片预览

文档简介
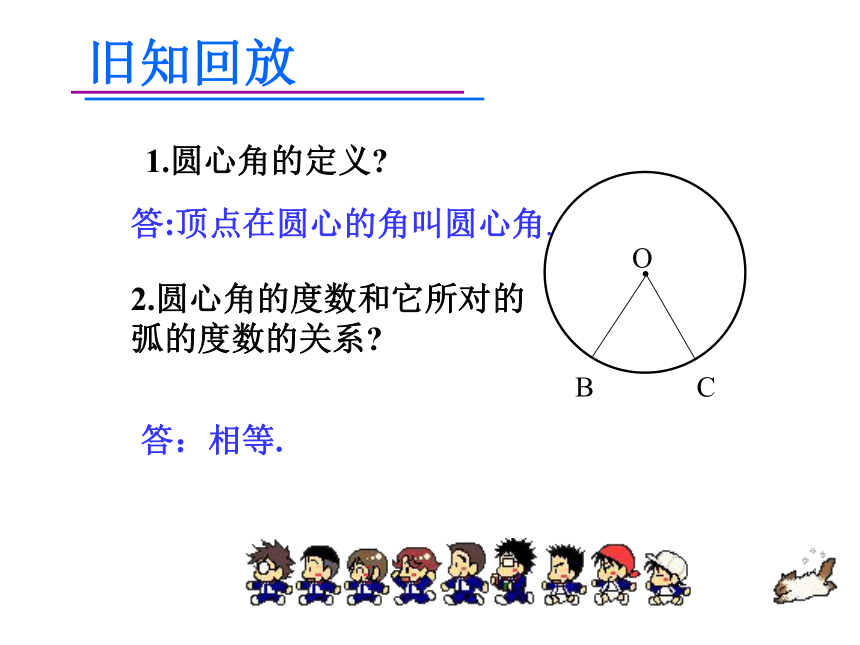
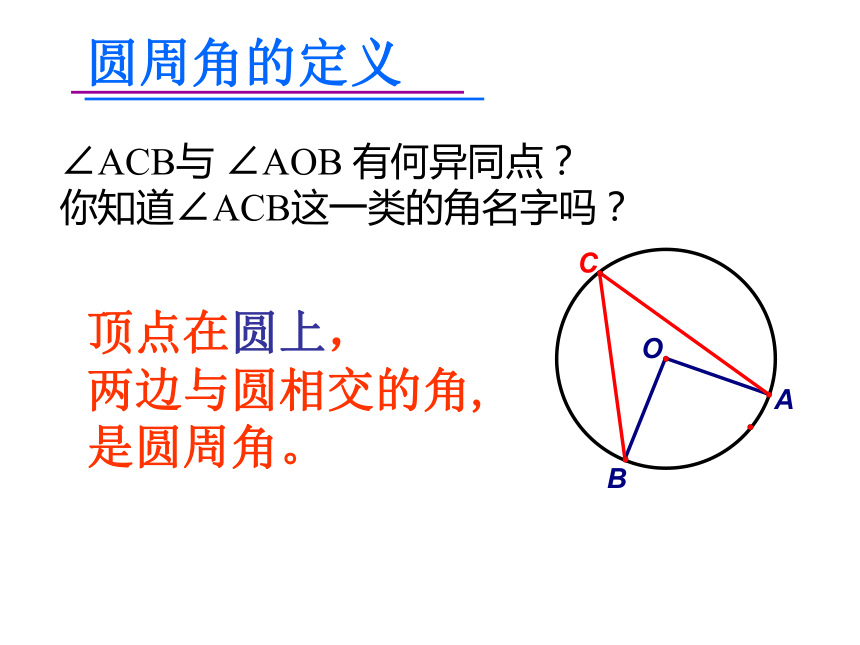
课件24张PPT。圆周角及圆周角定理旧知回放1.圆心角的定义?答:相等.答:顶点在圆心的角叫圆心角.2.圆心角的度数和它所对的弧的度数的关系?圆周角的定义∠ACB与 ∠AOB 有何异同点?
你知道∠ACB这一类的角名字吗? 顶点在圆上,
两边与圆相交的角,
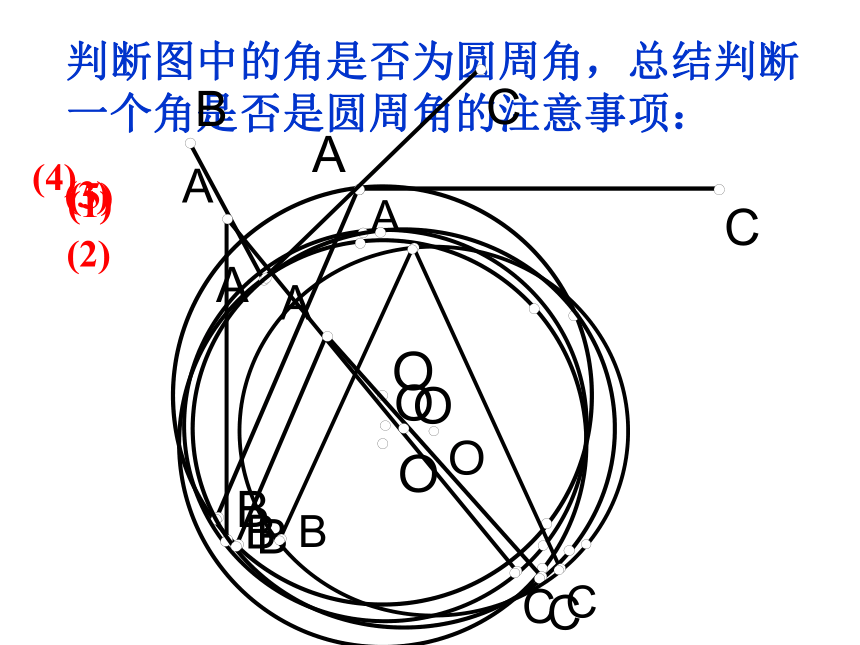
是圆周角。 判断图中的角是否为圆周角,总结判断
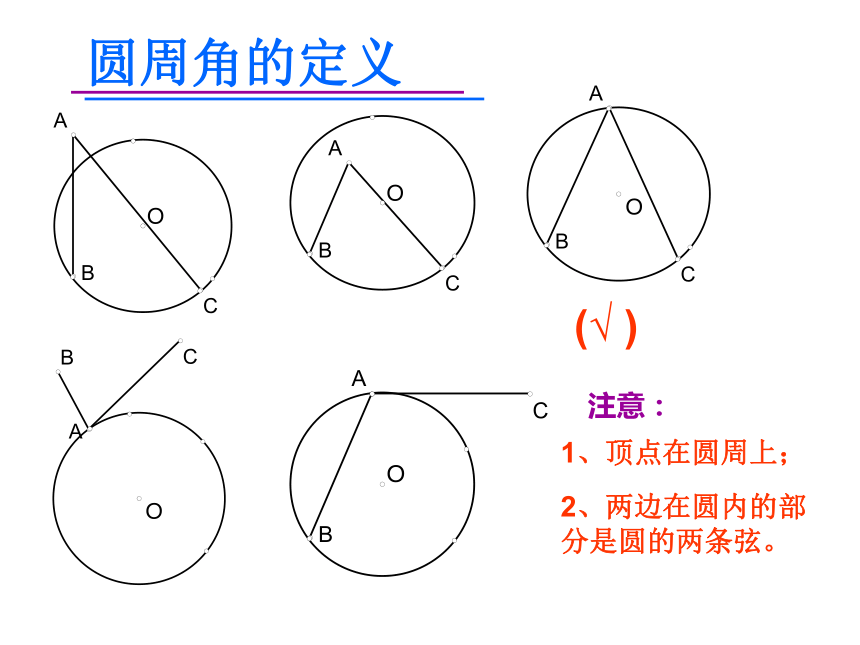
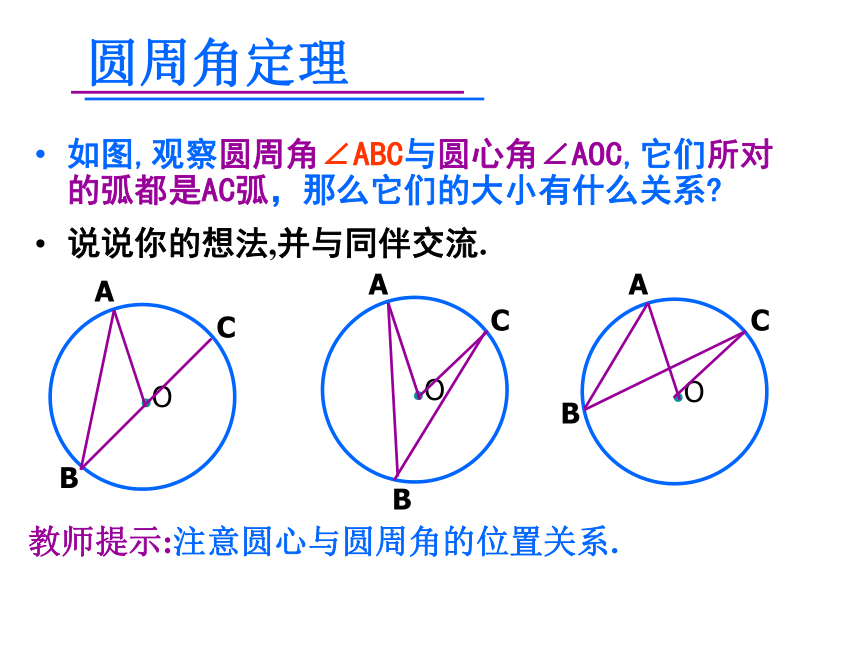
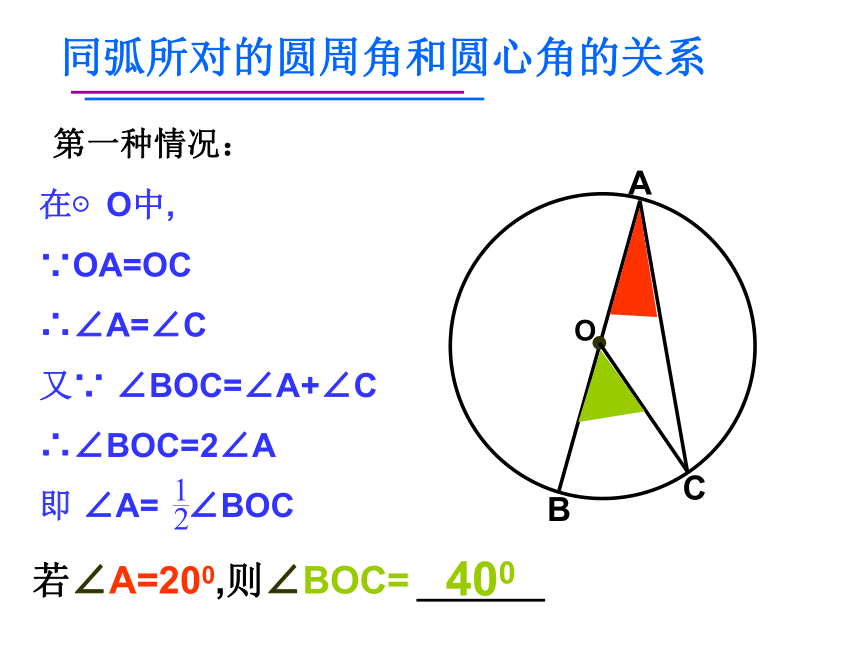
一个角是否是圆周角的注意事项:(1)(2)(3)(4)(5)(√ )圆周角的定义注意:1、顶点在圆周上;2、两边在圆内的部分是圆的两条弦。圆周角定理如图,观察圆周角∠ABC与圆心角∠AOC,它们所对的弧都是AC弧,那么它们的大小有什么关系?说说你的想法,并与同伴交流.教师提示:注意圆心与圆周角的位置关系.第一种情况:400同弧所对的圆周角和圆心角的关系在⊙O中,
∵OA=OC
∴∠A=∠C
又∵ ∠BOC=∠A+∠C
∴∠BOC=2∠A
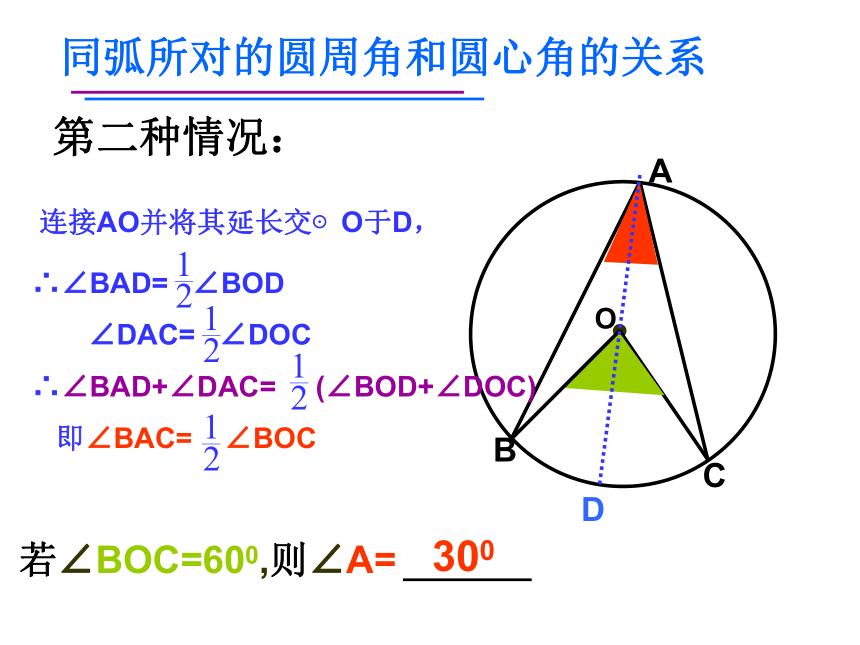
即 ∠A= ∠BOC OABC第二种情况:300同弧所对的圆周角和圆心角的关系连接AO并将其延长交⊙O于D,∴∠BAD= ∠BOD
∠DAC= ∠DOC
∴∠BAD+∠DAC= (∠BOD+∠DOC)
即∠BAC= ∠BOC
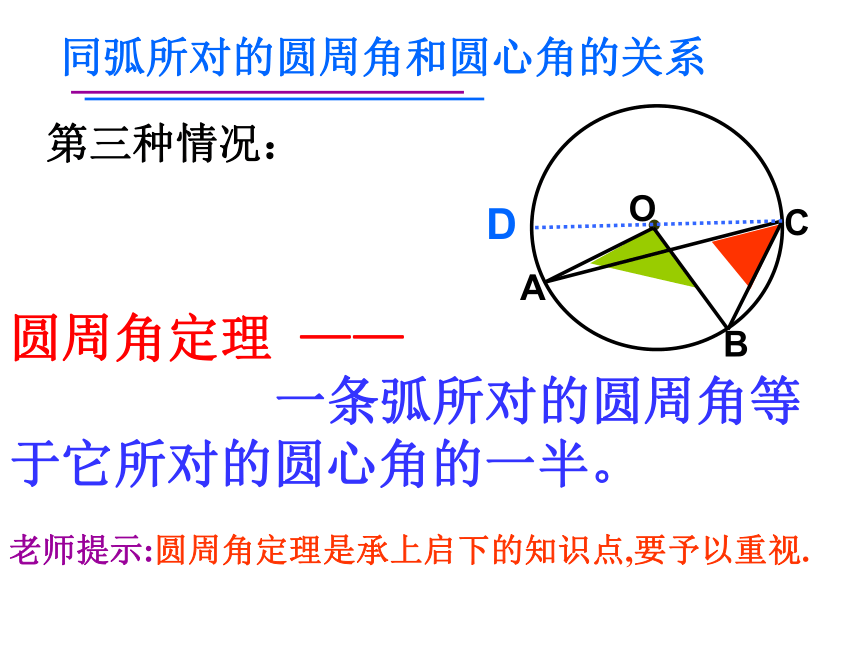
第三种情况:圆周角定理 ——
一条弧所对的圆周角等于它所对的圆心角的一半。同弧所对的圆周角和圆心角的关系老师提示:圆周角定理是承上启下的知识点,要予以重视.1.如图:圆心角∠BOC=60°,则圆周角∠BAC=_____;30060°巩固练习12.如图,圆周角∠BAC=25°,则圆心角∠BOC=____;5002503.如图,若弧BC的度数为40°,
则圆心角∠BOC=____;
圆周角∠BAC=____;
400200巩固练习15.如图,圆心角∠AOB=100°,则∠ACB=_ __。4.求圆中角X的度数130° C C B巩固练习16、判断
(1)顶点在圆上的角叫圆周角。( )
(2)圆周角的度数等于所对弧的度数的一半。( )
7、计算
半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是 。×√O60°或120°巩固练习1老师提示:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理。课本P103页1)100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。课后测验B
100o50o36o或144o64o100o圆周角定理的推论问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?∠B = ∠D= ∠E圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。用于找相等的弧用于找相等的角圆周角定理的推论问题2、如图2,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?∠BAC =90o圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;用于判断某条线是否过圆心圆周角定理的推论问题3、如图3,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?90°的圆周角所对的弦是直径。圆周角定理的推论2:用于判断某个圆周角是否是直角ABCD(1)(2).O.OABCCD.O.OABCD(3) 1. 在⊙o中,与∠BAC相等的角有( ).2.如图,在⊙O中,四边形ABCD的对角线把四个内角分
成的八个角中有( ) 相等的角.
3.如图,在⊙O中,直径AB=10㎝, ∠BAC=30°,则
AC=( ) ㎝.∠BDC四对 巩固练习2已知:如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E,(1)BD与CD的大小有什么关系?为什么?(2)求证:⌒ ⌒BD=DE理由是: 连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴ AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD = DE(同圆或等圆中相等的圆周角所对弧相等)。解:BD=CD.∴BD=CD,典型例题知识小结1.同弧或等弧所对的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧相等.
2.半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.教师提示:条件“同弧或等弧”改为“同弦或等弦”,
或删去“同圆或等圆”的条件,结论都不成立了.如图,圆O中,AB是直径,半径CO⊥ AB,D 是CO的中点,DE // AB,求:∠EBA思维拓展 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点, ∠ACB就是”危险角”,当船与两个灯塔的夹角大于”危险角”时,就有可能触礁.(1)当船与两个灯塔的夹角∠a大于”危险角”时,船位于哪个区域?为什么?(1)当船与两个灯塔的夹角∠a小于”危险角”时,船位于哪个区域?为什么?实践应用结束寄语要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.再见
你知道∠ACB这一类的角名字吗? 顶点在圆上,
两边与圆相交的角,
是圆周角。 判断图中的角是否为圆周角,总结判断
一个角是否是圆周角的注意事项:(1)(2)(3)(4)(5)(√ )圆周角的定义注意:1、顶点在圆周上;2、两边在圆内的部分是圆的两条弦。圆周角定理如图,观察圆周角∠ABC与圆心角∠AOC,它们所对的弧都是AC弧,那么它们的大小有什么关系?说说你的想法,并与同伴交流.教师提示:注意圆心与圆周角的位置关系.第一种情况:400同弧所对的圆周角和圆心角的关系在⊙O中,
∵OA=OC
∴∠A=∠C
又∵ ∠BOC=∠A+∠C
∴∠BOC=2∠A
即 ∠A= ∠BOC OABC第二种情况:300同弧所对的圆周角和圆心角的关系连接AO并将其延长交⊙O于D,∴∠BAD= ∠BOD
∠DAC= ∠DOC
∴∠BAD+∠DAC= (∠BOD+∠DOC)
即∠BAC= ∠BOC
第三种情况:圆周角定理 ——
一条弧所对的圆周角等于它所对的圆心角的一半。同弧所对的圆周角和圆心角的关系老师提示:圆周角定理是承上启下的知识点,要予以重视.1.如图:圆心角∠BOC=60°,则圆周角∠BAC=_____;30060°巩固练习12.如图,圆周角∠BAC=25°,则圆心角∠BOC=____;5002503.如图,若弧BC的度数为40°,
则圆心角∠BOC=____;
圆周角∠BAC=____;
400200巩固练习15.如图,圆心角∠AOB=100°,则∠ACB=_ __。4.求圆中角X的度数130° C C B巩固练习16、判断
(1)顶点在圆上的角叫圆周角。( )
(2)圆周角的度数等于所对弧的度数的一半。( )
7、计算
半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是 。×√O60°或120°巩固练习1老师提示:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理。课本P103页1)100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。课后测验B
100o50o36o或144o64o100o圆周角定理的推论问题1、如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?∠B = ∠D= ∠E圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。用于找相等的弧用于找相等的角圆周角定理的推论问题2、如图2,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?∠BAC =90o圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;用于判断某条线是否过圆心圆周角定理的推论问题3、如图3,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?90°的圆周角所对的弦是直径。圆周角定理的推论2:用于判断某个圆周角是否是直角ABCD(1)(2).O.OABCCD.O.OABCD(3) 1. 在⊙o中,与∠BAC相等的角有( ).2.如图,在⊙O中,四边形ABCD的对角线把四个内角分
成的八个角中有( ) 相等的角.
3.如图,在⊙O中,直径AB=10㎝, ∠BAC=30°,则
AC=( ) ㎝.∠BDC四对 巩固练习2已知:如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E,(1)BD与CD的大小有什么关系?为什么?(2)求证:⌒ ⌒BD=DE理由是: 连结AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴ AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD = DE(同圆或等圆中相等的圆周角所对弧相等)。解:BD=CD.∴BD=CD,典型例题知识小结1.同弧或等弧所对的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧相等.
2.半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.教师提示:条件“同弧或等弧”改为“同弦或等弦”,
或删去“同圆或等圆”的条件,结论都不成立了.如图,圆O中,AB是直径,半径CO⊥ AB,D 是CO的中点,DE // AB,求:∠EBA思维拓展 船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁,如图,A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点, ∠ACB就是”危险角”,当船与两个灯塔的夹角大于”危险角”时,就有可能触礁.(1)当船与两个灯塔的夹角∠a大于”危险角”时,船位于哪个区域?为什么?(1)当船与两个灯塔的夹角∠a小于”危险角”时,船位于哪个区域?为什么?实践应用结束寄语要养成用数学的语言去说明道理,用数学的思维去解读世界的习惯.再见
