弦、
图片预览

文档简介
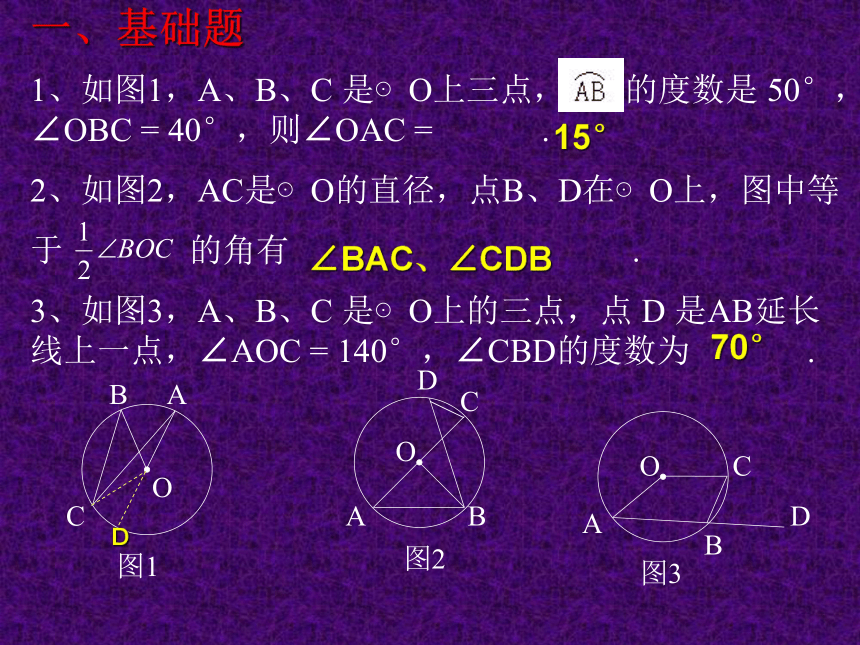
课件13张PPT。弦、弧、圆心角、圆周角习题课1、如图1,A、B、C 是⊙O上三点, 的度数是 50°,∠OBC = 40°,则∠OAC = .
2、如图2,AC是⊙O的直径,点B、D在⊙O上,图中等
于 的角有 .
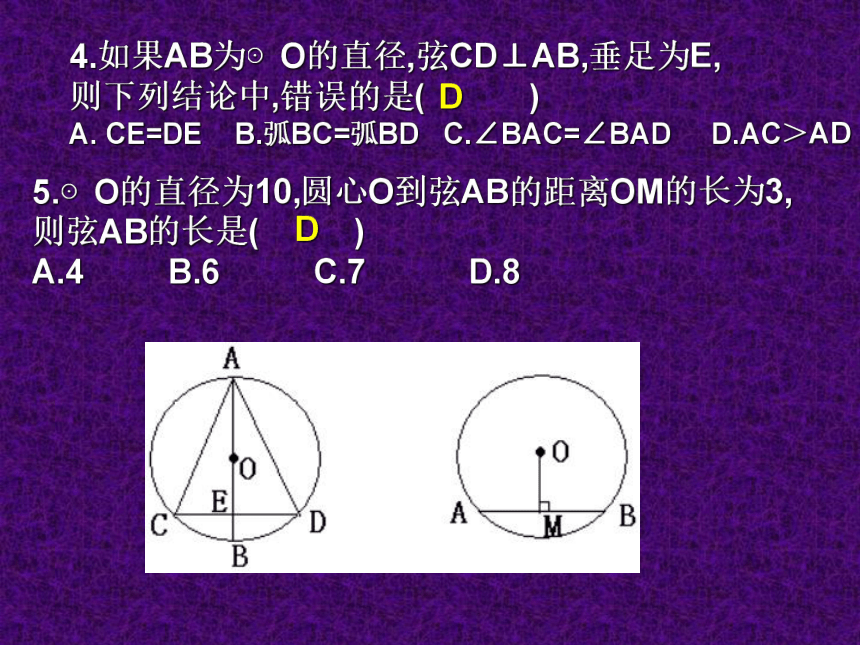
3、如图3,A、B、C 是⊙O上的三点,点 D 是AB延长线上一点,∠AOC = 140°,∠CBD的度数为 .图1ACBOAOBCD图2图3OBCAD15°∠BAC、∠CDB70°D一、基础题4.如果AB为⊙O的直径,弦CD⊥AB,垂足为E,
则下列结论中,错误的是( )
A. CE=DE B.弧BC=弧BD C.∠BAC=∠BAD D.AC>AD5.⊙O的直径为10,圆心O到弦AB的距离OM的长为3,
则弦AB的长是( )
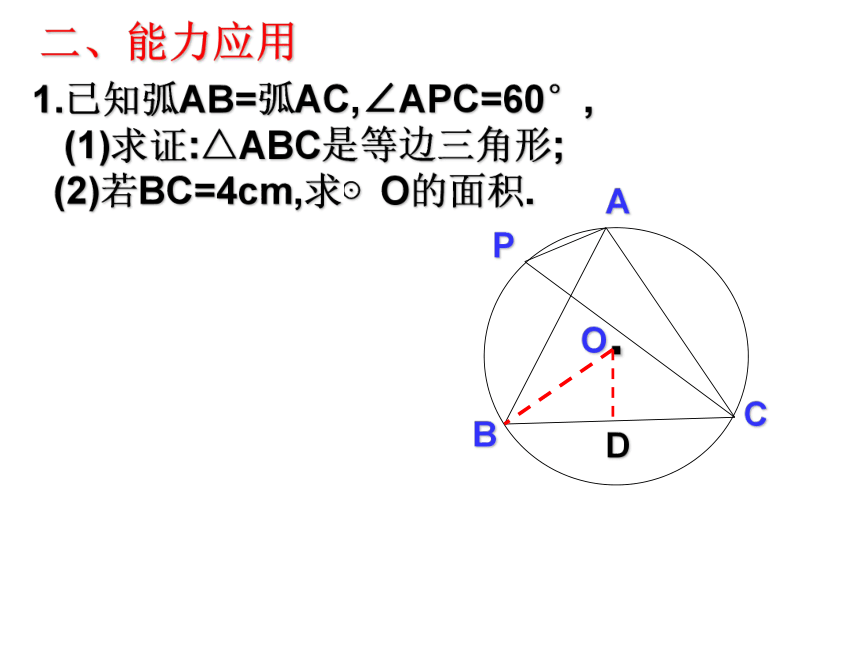
A.4 B.6 C.7 D.8DD1.已知弧AB=弧AC,∠APC=60°,
(1)求证:△ABC是等边三角形;
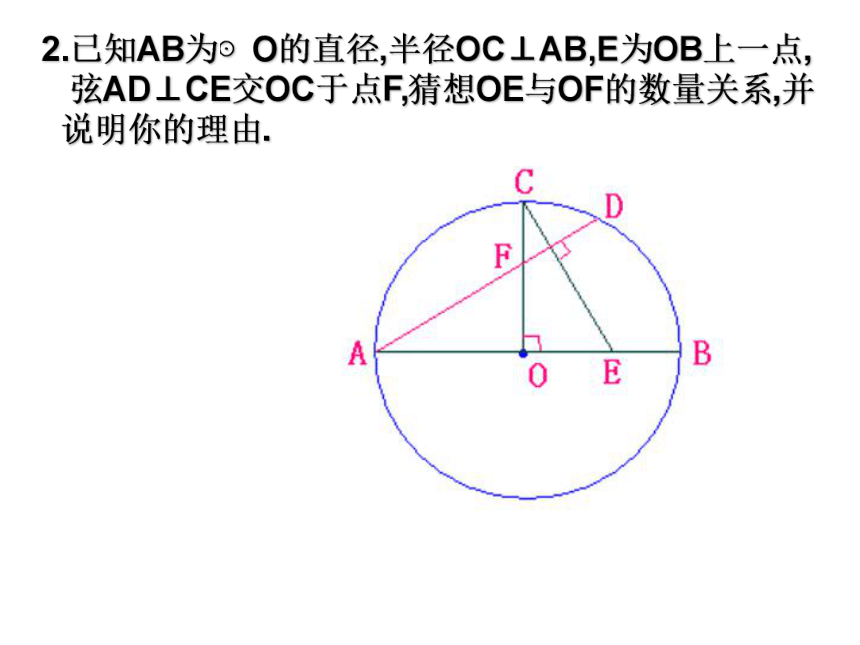
(2)若BC=4cm,求⊙O的面积..APOBCD二、能力应用2.已知AB为⊙O的直径,半径OC⊥AB,E为OB上一点,
弦AD⊥CE交OC于点F,猜想OE与OF的数量关系,并
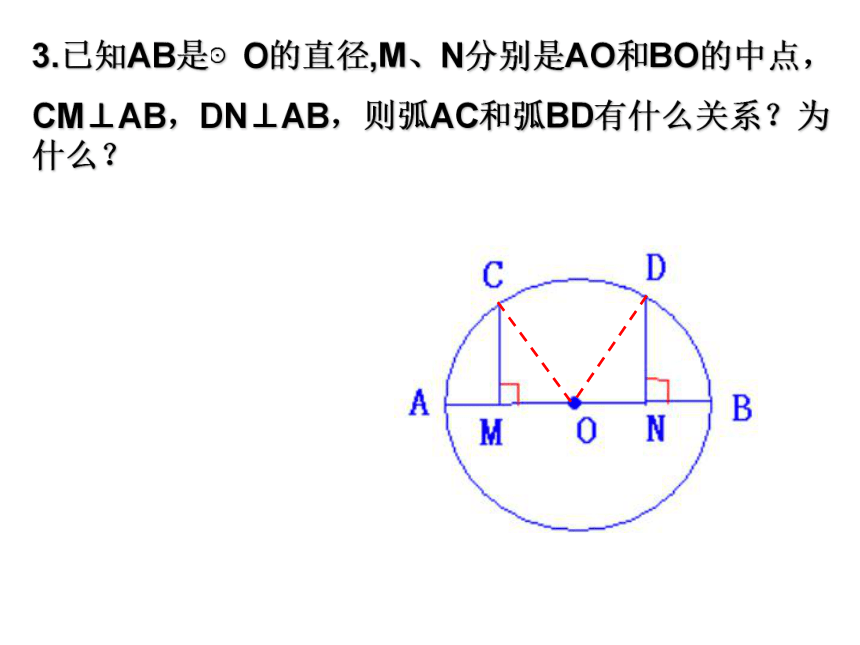
说明你的理由.3.已知AB是⊙O的直径,M、N分别是AO和BO的中点,
CM⊥AB,DN⊥AB,则弧AC和弧BD有什么关系?为什么?⊙⊙EF5.A、B、C是⊙O上三个点,连接弧AB和弧AC
的中点D、E的弦交弦AB、AC于F、G,试
判断△AFG的形状.6.在足球比赛场上,甲、乙两名队员互相配合向对方
球门MN进攻,当甲带球攻到球门前A处时,乙已跟随
冲到B点.这里甲是选择自己攻门好,还是迅速将球
传给乙,让乙射门?解:球场上的情况是很复杂的,球员射门
常会选择较好的射门角度.这就要
看A、B两点各自对球门MN的张角
的大小,当张角较小时,则球容易
被对方守门员截住.因此,只需比较
∠MAN与∠MBN的大小.
过M、N点及B点作一个⊙O,即⊙O过点B、M、N,
显然点A在⊙O外,设AM交圆O于C,则
∠MAN<∠MCN=∠MBN。因此,在B点射门较好。MN7.⊙C经过坐标原点,且与两坐标轴分别交于
点A、B,点A的坐标为(0,4),M是圆上
一点,∠BMO=120°.
(1)求证:AB为⊙c的直径.
(2)求⊙C的半径及圆心C的坐标.DE8.我们定义:顶点在圆外,并且两边都和圆相交的角叫
圆外角.如图,∠DPB是圆外角,那么∠DPB的度数与
它所夹的两段弧BD弧AC的度数有什么关系?
(1)你的结论用文字表述为(不准出现字母和数学符号)
_______________________________________
__________________;
(2)证明你的结论.圆外角的度数等于它所夹的两段大弧与小弧的
度数差的一半.9.BC为⊙O的直径,AD⊥BC于点D,P是弧AC上的一动点,
连结PB分别交AD、AC于点E,F。
(1)当弧PA=弧AB时,求证:AE=BE;
(2)当点P在什么位置时,AF=EF?证明你的结论。动脑、动手才有收获
2、如图2,AC是⊙O的直径,点B、D在⊙O上,图中等
于 的角有 .
3、如图3,A、B、C 是⊙O上的三点,点 D 是AB延长线上一点,∠AOC = 140°,∠CBD的度数为 .图1ACBOAOBCD图2图3OBCAD15°∠BAC、∠CDB70°D一、基础题4.如果AB为⊙O的直径,弦CD⊥AB,垂足为E,
则下列结论中,错误的是( )
A. CE=DE B.弧BC=弧BD C.∠BAC=∠BAD D.AC>AD5.⊙O的直径为10,圆心O到弦AB的距离OM的长为3,
则弦AB的长是( )
A.4 B.6 C.7 D.8DD1.已知弧AB=弧AC,∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)若BC=4cm,求⊙O的面积..APOBCD二、能力应用2.已知AB为⊙O的直径,半径OC⊥AB,E为OB上一点,
弦AD⊥CE交OC于点F,猜想OE与OF的数量关系,并
说明你的理由.3.已知AB是⊙O的直径,M、N分别是AO和BO的中点,
CM⊥AB,DN⊥AB,则弧AC和弧BD有什么关系?为什么?⊙⊙EF5.A、B、C是⊙O上三个点,连接弧AB和弧AC
的中点D、E的弦交弦AB、AC于F、G,试
判断△AFG的形状.6.在足球比赛场上,甲、乙两名队员互相配合向对方
球门MN进攻,当甲带球攻到球门前A处时,乙已跟随
冲到B点.这里甲是选择自己攻门好,还是迅速将球
传给乙,让乙射门?解:球场上的情况是很复杂的,球员射门
常会选择较好的射门角度.这就要
看A、B两点各自对球门MN的张角
的大小,当张角较小时,则球容易
被对方守门员截住.因此,只需比较
∠MAN与∠MBN的大小.
过M、N点及B点作一个⊙O,即⊙O过点B、M、N,
显然点A在⊙O外,设AM交圆O于C,则
∠MAN<∠MCN=∠MBN。因此,在B点射门较好。MN7.⊙C经过坐标原点,且与两坐标轴分别交于
点A、B,点A的坐标为(0,4),M是圆上
一点,∠BMO=120°.
(1)求证:AB为⊙c的直径.
(2)求⊙C的半径及圆心C的坐标.DE8.我们定义:顶点在圆外,并且两边都和圆相交的角叫
圆外角.如图,∠DPB是圆外角,那么∠DPB的度数与
它所夹的两段弧BD弧AC的度数有什么关系?
(1)你的结论用文字表述为(不准出现字母和数学符号)
_______________________________________
__________________;
(2)证明你的结论.圆外角的度数等于它所夹的两段大弧与小弧的
度数差的一半.9.BC为⊙O的直径,AD⊥BC于点D,P是弧AC上的一动点,
连结PB分别交AD、AC于点E,F。
(1)当弧PA=弧AB时,求证:AE=BE;
(2)当点P在什么位置时,AF=EF?证明你的结论。动脑、动手才有收获
