圆周角
图片预览


文档简介
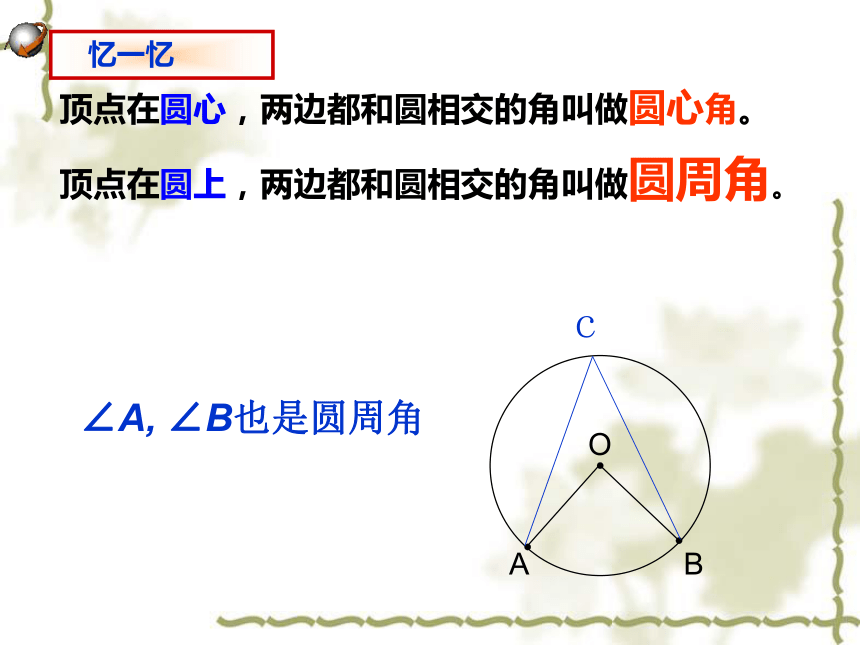
课件14张PPT。23.1.3 圆周角顶点在圆上,两边都和圆相交的角叫做圆周角。
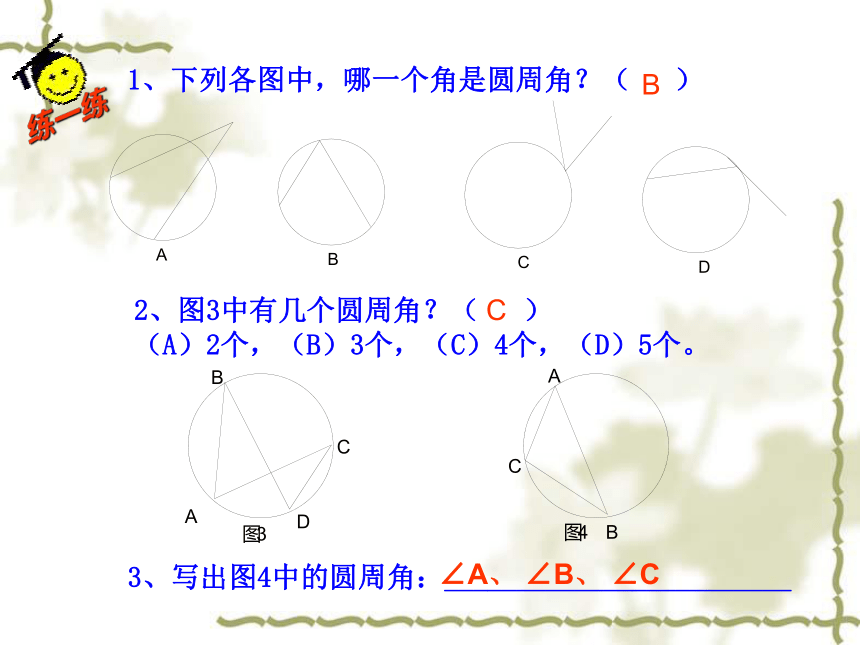
顶点在圆心,两边都和圆相交的角叫做圆心角。∠A, ∠B也是圆周角 练一练1、下列各图中,哪一个角是圆周角?( )
2、图3中有几个圆周角?( )
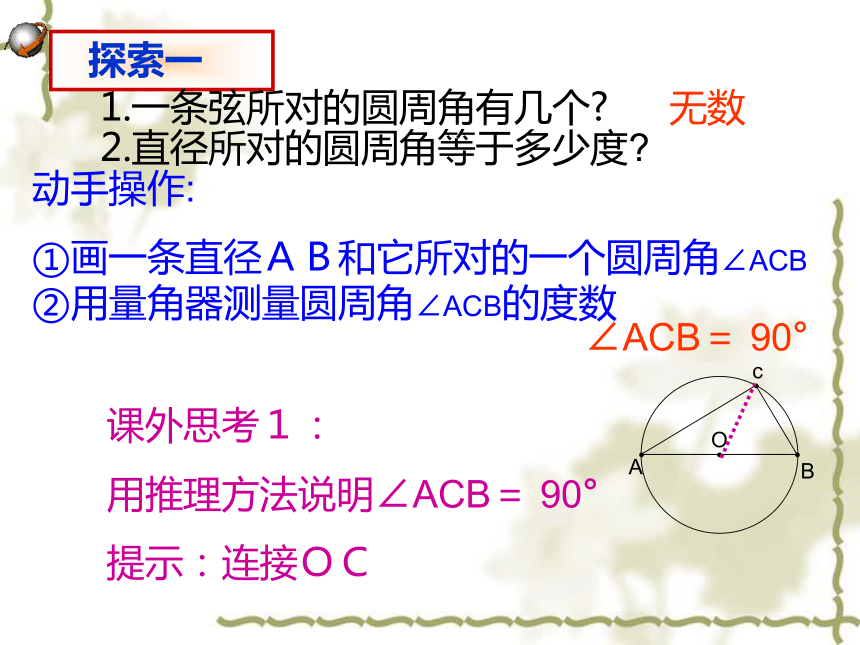
(A)2个,(B)3个,(C)4个,(D)5个。3、写出图4中的圆周角:________________________BC∠A、 ∠B、 ∠C1.一条弦所对的圆周角有几个? 无数2.直径所对的圆周角等于多少度?动手操作:
①画一条直径AB和它所对的一个圆周角∠ACB ②用量角器测量圆周角∠ACB的度数∠ACB= 90°课外思考1:
用推理方法说明∠ACB= 90°
提示:连接OC 结论1:半圆或直径所对的圆周角都相等, 都等于90°(直角) 90°的圆周角所对的弦是圆的直径例1 如图,AB为⊙O的直径,∠A=80°
求∠B的度数。ABO解:∵AB为⊙O的直径
∴∠C=90°
又∵ ∠A=80°
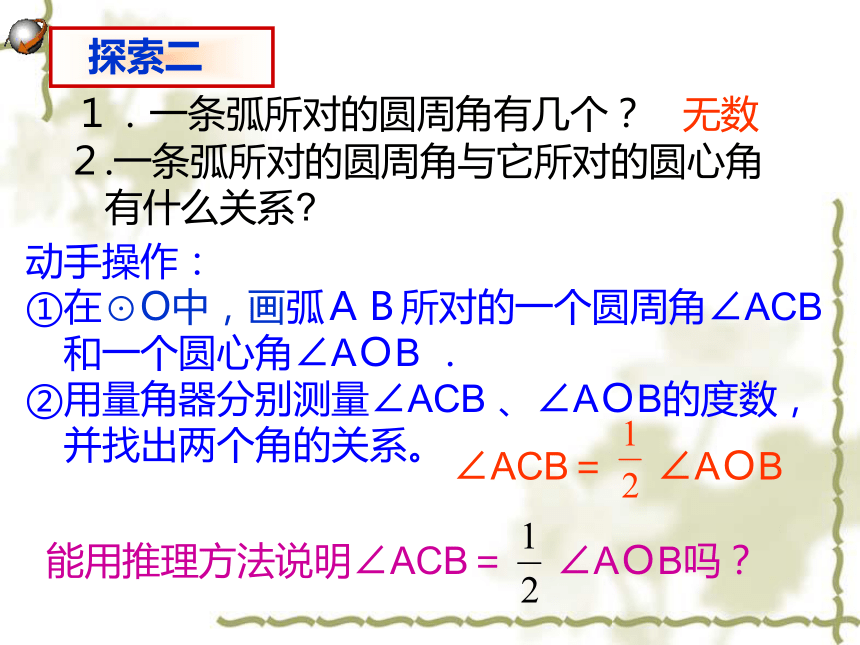
∴∠B=180°-∠A-∠C=10°1.一条弧所对的圆周角有几个?无数2.一条弧所对的圆周角与它所对的圆心角
有什么关系?动手操作:
①在⊙O中,画弧AB所对的一个圆周角∠ACB
和一个圆心角∠AOB .
②用量角器分别测量∠ACB 、∠AOB的度数,
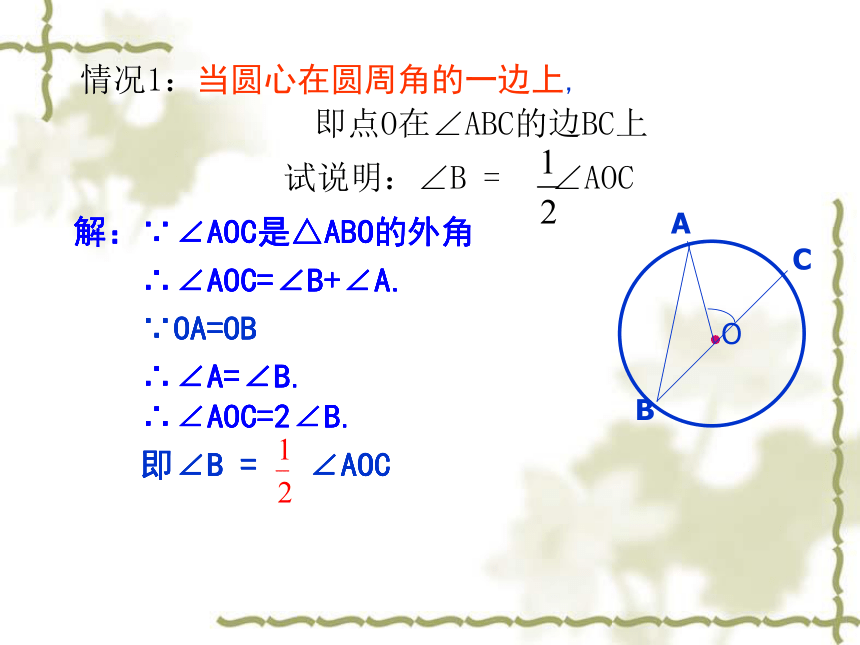
并找出两个角的关系。 ∠ACB= ∠AOB能用推理方法说明∠ACB= ∠AOB吗?情况1:当圆心在圆周角的一边上,
即点O在∠ABC的边BC上解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC试说明:∠B = ∠AOC解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC提示:能不能转化为第1种情况?解:作直径BD∠1 = ∠3,
∠2= ∠4,情况2:当圆心在圆周角内部,
即点O在∠ABC 内试说明: ∠ABC = ∠AOC由第一种情况可得 ∴∠1+ ∠2 = (∠3+∠4)
即∠ABC = ∠AOC.课外思考2
情况3:当圆心在圆周角外部,
即点O在∠ABC 内试说明: ∠ABC = ∠AOC提示:过点B作直径BD,
转化为第一种情况 结论2: 在同一圆内,一条弧所对的圆周 角等于它所对的圆心角的一半. 练一练1、如图6,已知∠ACB = 20o,
则∠AOB = _____, ∠OAB =
40o70o130o2、如图7,已知圆心角∠AOB=100°,
则∠ACB = _______。练习:P51. 第1题,第2题结论3:同圆内,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧相等。 我的收获这节课你有哪些收获?(1)一个概念(圆周角)(2)三个结论
1.半圆或直径所对的圆周角是直角;
90°的圆周角所对的弦是直径。
2.在一个圆中, 一条弧所对的圆周角等于该弧所对的圆心角的一半;
3. 同圆内,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧相等。
1.作业:(必做题)P52.第6题 第7题
2.(自选题)如图8,OA、OB、OC都是圆O的
半径,∠AOB = 2∠BOC
求证:∠ACB = 2∠BAC.多谢指导
顶点在圆心,两边都和圆相交的角叫做圆心角。∠A, ∠B也是圆周角 练一练1、下列各图中,哪一个角是圆周角?( )
2、图3中有几个圆周角?( )
(A)2个,(B)3个,(C)4个,(D)5个。3、写出图4中的圆周角:________________________BC∠A、 ∠B、 ∠C1.一条弦所对的圆周角有几个? 无数2.直径所对的圆周角等于多少度?动手操作:
①画一条直径AB和它所对的一个圆周角∠ACB ②用量角器测量圆周角∠ACB的度数∠ACB= 90°课外思考1:
用推理方法说明∠ACB= 90°
提示:连接OC 结论1:半圆或直径所对的圆周角都相等, 都等于90°(直角) 90°的圆周角所对的弦是圆的直径例1 如图,AB为⊙O的直径,∠A=80°
求∠B的度数。ABO解:∵AB为⊙O的直径
∴∠C=90°
又∵ ∠A=80°
∴∠B=180°-∠A-∠C=10°1.一条弧所对的圆周角有几个?无数2.一条弧所对的圆周角与它所对的圆心角
有什么关系?动手操作:
①在⊙O中,画弧AB所对的一个圆周角∠ACB
和一个圆心角∠AOB .
②用量角器分别测量∠ACB 、∠AOB的度数,
并找出两个角的关系。 ∠ACB= ∠AOB能用推理方法说明∠ACB= ∠AOB吗?情况1:当圆心在圆周角的一边上,
即点O在∠ABC的边BC上解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC试说明:∠B = ∠AOC解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC解:∵∠AOC是△ABO的外角
∴∠AOC=∠B+∠A.
∵OA=OB
∴∠A=∠B.
∴∠AOC=2∠B.
即∠B = ∠AOC提示:能不能转化为第1种情况?解:作直径BD∠1 = ∠3,
∠2= ∠4,情况2:当圆心在圆周角内部,
即点O在∠ABC 内试说明: ∠ABC = ∠AOC由第一种情况可得 ∴∠1+ ∠2 = (∠3+∠4)
即∠ABC = ∠AOC.课外思考2
情况3:当圆心在圆周角外部,
即点O在∠ABC 内试说明: ∠ABC = ∠AOC提示:过点B作直径BD,
转化为第一种情况 结论2: 在同一圆内,一条弧所对的圆周 角等于它所对的圆心角的一半. 练一练1、如图6,已知∠ACB = 20o,
则∠AOB = _____, ∠OAB =
40o70o130o2、如图7,已知圆心角∠AOB=100°,
则∠ACB = _______。练习:P51. 第1题,第2题结论3:同圆内,同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧相等。 我的收获这节课你有哪些收获?(1)一个概念(圆周角)(2)三个结论
1.半圆或直径所对的圆周角是直角;
90°的圆周角所对的弦是直径。
2.在一个圆中, 一条弧所对的圆周角等于该弧所对的圆心角的一半;
3. 同圆内,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧相等。
1.作业:(必做题)P52.第6题 第7题
2.(自选题)如图8,OA、OB、OC都是圆O的
半径,∠AOB = 2∠BOC
求证:∠ACB = 2∠BAC.多谢指导
