人教版八年级下册 19.2.1正比例函数巩固培优练 含答案
文档属性
| 名称 | 人教版八年级下册 19.2.1正比例函数巩固培优练 含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 333.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 21:58:06 | ||
图片预览




文档简介
19.2.1 正比例函数 巩固培优练
一、单选题
1.下列说法中,不正确的是( ).
A.在中,是的正比例函数
B.在中,是的正比例函数
C.在=3中,是的正比例函数
D.正方形的边长与周长为正比例关系
2.直线y=﹣2x+5与x轴、y轴的交点坐标分别是( )
A.(,0),(0,5) B.(﹣,0),(0,5)
C.(,0),(0,﹣5) D.(﹣,0),(0,﹣5)
3.点和点都在直线上,则与的关系是( )
A. B. C. D.
4.已知函数y=x+k+1是正比例函数,则k的值为( )
A.1 B.﹣1 C.0 D.±1
5.若函数是正比例函数,则下列叙述正确的是( )
A. B. C. D.y随x的增大而增大
6.已知是关于x的正比例函数,则m的值为( )
A.2 B.1 C.0或2 D.0
7.函数的图象与、y轴的交点为A、B,则AB等于 ( )
A. B.2 C.2 D.5
8.已知正比例函数y=(2m-1)x的图象上两点A(-1,y1),B(2,y2),且有y1>y2,那么m的取值范围是( )
A.m< B.m> C.m<2 D.m>2
9.在平面直角坐标系中,对于平面内一点(m,n)规定以下两种变换,
①f(m,n)=(m,–n),如f(2,1)=(2,–1);
②g(m,n)=(–m,–n),如g(2,1)=(–2,–1).
按照以上变换,则经过点f[g(3,4)],点g[f(–3,2)]的直线方程为()
A.y=–x+3 B.y=x+3 C.y=–x–3 D.y=x–3
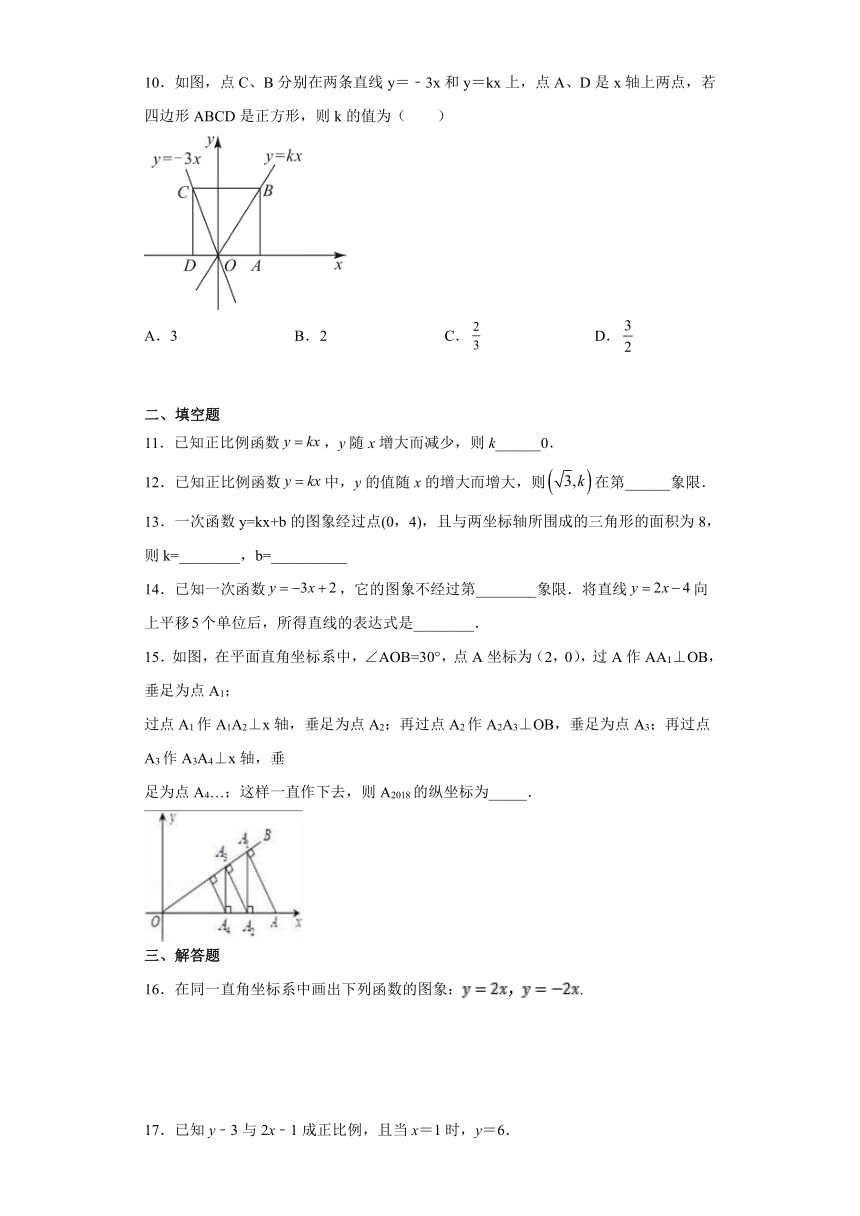
10.如图,点C、B分别在两条直线y=﹣3x和y=kx上,点A、D是x轴上两点,若四边形ABCD是正方形,则k的值为( )
A.3 B.2 C. D.
二、填空题
11.已知正比例函数,y随x增大而减少,则k______0.
12.已知正比例函数中,y的值随x的增大而增大,则在第______象限.
13.一次函数y=kx+b的图象经过点(0,4),且与两坐标轴所围成的三角形的面积为8,则k=________,b=__________
14.已知一次函数,它的图象不经过第________象限.将直线向上平移个单位后,所得直线的表达式是________.
15.如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;
过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂
足为点A4…;这样一直作下去,则A2018的纵坐标为_____.
三、解答题
16.在同一直角坐标系中画出下列函数的图象:.
17.已知y﹣3与2x﹣1成正比例,且当x=1时,y=6.
(1)求y与x之间的函数解析式.
(2)当x=2时,求y的值.
(3)若点A(x1,y1),B(x2,y2)都在该函数的图象上,且y1>y2,试判断x1,x2的大小关系.
18.2017年12月29日郑州市人民政府通告:为减少机动车污染物排放,持续改善我市空气质量,从2018年1月1日起,每周工作日的7时至21时郑州市东三环、南三环、西三环、北三环以内区域的所有道路限行按机动车号牌(含临时号牌和外地号牌)最后一位阿拉伯数字(尾数为字母的以末尾数字为准),工作日每天限行2个号,即:号码最后一位阿拉伯数字为1和6的机动车周一限行,2和7的机动车周二限行,3和8的机动车周三限4和9的机动车周四限行,5和0的机动车周五限行,因法定节假日放假、调休而调整为上班的周六、周日按对应调体的工作日限行但通告中还规定,悬挂新能源专用牌的新能源汽车不受限制.限行通告发布后,新能源汽车成为畅销车型,某4S店销售每辆进价分别为5万元、9万元的A、B两种型号的新能源汽车,下表是近两周的销售情况:
(1)求A、B两种型号的新能源汽车的销售单价;(共
(2)若4S店准备用不超过200万元的金额采购这两种型号的新能源汽车共30辆,求B型号的新能源汽车最多能采购多少辆
(进价、售价均保持不变,利润=销售收入一进货成本)
(3在(2)的条件下,4S销售完这230辆新能源汽车时45店的最大利润是多少 并写
19.下表给出了一次函数y=kx+b(k≠0)中y与x的部分对应值.
x … -2 -1 5 …
y … 1 -1 -12 …
(1)根据表中的数据,确定一次函数的表达式;
(2)点(2,-5)是否在这个一次函数的图象上?请说明理由.
20.在平面直角坐标系中,对任意的点P(x,y),定义P的绝对坐标|P|=|x|+|y|.任取点A(x1,y1),B(x2,y2),记(x1,y2),(x2,y1),若此时|A|2+|B|2≤||2+||2成立,则称点A,B相关.
(1)分别判断下面各组中两点是相关点的是 ;
①A(﹣2,1),B(3,2);②C(4,﹣3),D(2,4).
(2)①对于点P(x,y),其中﹣6≤x≤6,﹣6≤y≤6,其中x,y是整数.则所有满足条件的P点有 个;
②求所有满足①条件的所有点中与点E(3,3)相关的点的个数;
③对于满足①条件的所有点中取出n个点,满足在这n个点中任意选择A,B两点,点A,B都相关,求n的最大值.
参考答案
1.A
2.A
3.A
4.B
5.C
6.D
7.B
8.A
9.A
10.D
11.<
12.一
13. ±1 4
14. 三, y=2x+1
15.
16.解:根据一次函数的特点,的图象过原点,且过点(1,2),
同理,的图象过原点,且过点(1,).
又由其图象为直线,作出图象如图所示.
17.解:(1)设y﹣3=k(2x﹣1),
把x=1,y=6代入得6﹣3=k(2×1﹣1),解得k=3,
则y﹣3=3(2x﹣1),
所以y与x之间的函数解析式为y=6x;
(2)由(1)知,y=6x
∴当x=2x时,y=6=12;
(3)∵,
而,
∴
∴
18.分析: (1)设A, B两种型号的新能源汽车的销售单价分别为x元,y元,根据表格中的等量关系可得 解得 ,(2) 设B型号的新能源汽车a辆,则采购A型号的新能源汽车 (30-a)辆,根据采购两种车辆的金额不超过200万元可列不等式
10a+5.8(30-a)≤200, 解得: a≤12.5,根据实际情况取整,
(3) 设4S店销售完这30辆车,获得的利润是万元,根据总利润=A型号的销售利润+B型号的销售利润,可得:,
详解:(1)设A, B两种型号的新能源汽车的销售单价分别为x元、y元,依题意得:
解得
答:A型汽车的销售单价为5.8万元,B型汽车的销售单价为10万元,
(2)设B型号的新能源汽车a辆,则采购A型号的新能源汽车 (30-a)辆,依题意得:
10a+5.8(30-a)≤200, 解得: a≤12.5. (a取整数),
答:4S店最多采购B型号的新能源汽车12辆.
(3)设4S店销售完这30辆车,获得的利润是万元,
,
,
w随a的增大而增大,
∴a最大时,w最大,
∵,且a是整数,
∴a=12时,w=24+0.2×12=26.4.
答:A型号采购18辆,B型号采购12辆时,利润最大,最大利润是26.4万元.
19.分析:(1)根据待定系数法求得即可;
(2)把点(2,﹣5)代入解析式即可判断.
详解:(1)根据题意得:,
解得:,所以一次函数的表达式为:y=﹣2x﹣3;
(2)点(2,﹣5)不在函数y=﹣2x﹣3的图象上.理由如下:
当x=2时,y=﹣2×2﹣3=﹣7≠﹣5,所以点(2,﹣5)不在函数y=﹣2x﹣3的图象上.
20.解:(1)①A(﹣2,1),B(3,2);A′(-2,2),B′(3,1),
∴,
∴;,
∵>,
∴①不是相关点,
②C(4,﹣3),D(2,4),,
,
∴;,
∵<,
∴②是相关点;
故答案为:②;
(2)①对于点P(x,y),其中﹣6≤x≤6,﹣6≤y≤6,其中x,y是整数.
∴x=-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,共13个整数,
∴y=-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,共13个整数,
所有满足条件的P(x,y)共有13×13=169个,
故答案为169;
②点E(3,3),设点Q(m,n)其中﹣6≤m≤6,﹣6≤n≤6,其中m,n是整数.
∵点E,Q是相关点,
∴,
整理得:,
因式分解得:,
∴或,
由得出两组解,
当时,
m=-3,-2,-1,0,1,2,3;n=-3,-4,-5,-6,7×4=28个;
当时,
m=-3,-2,-1,0,1,2,3;n=3,4,5,6,7×4=28个;
由,得出两组解,
当时,
m=-3,-4,-5,-6,n=-3,-2,-1,0,1,2,3;4×7=28个;
当时,
m=3,4,5,6,n=-3,-2,-1,0,1,2,3;4×7=28个;
(3,3)(3,-3)(-3,-3)(-3,3)各用两次,
所有与点E(3,3)相关的点的个数有4×28-4=108个,
故答案为108;
③设点A(x,y)其中﹣6≤x≤6,﹣6≤y≤6,其中x,y是整数,B(m,k)其中﹣6≤m≤6,﹣6≤k≤6,其中m,k是整数.
∵A、B是相关点,
∴,
整理得:,
因式分解得:,
或,
∴或,
∴或或或,
∴当x=y时,四点,组成正方形,由对角线y=x与y=-x,分成四个部分,每个部分中满足条件或或或是在每部分中长方形区域,在区域内都满足任意两点都是相关点,
每个区域中都有两个点在与上,当点P(x,y),
当x=y=0时,为坐标轴上点,4个区域中,每个区域有7个点,4各区域有(7-1)×4+1=25个,
当x=y=1时,正方形四个顶点为(1,1),(-1,1),(-1,-1),(1,-1),对角线分成4个区域中,正方形每边有3点,每个区域有三行,每行有6个点,每个区域有6×3=18个点,4个区域有(18-1)×4=68个,
当x=y=2时,正方形四个顶点为(2,2),(-2,2),(-2,-2),(2,-2),对角线分成4个区域中,正方形每边有5点,每个区域有五行,每行有5个点,4个区域中,每个区域有5×5=25个点,4个区域有(25-1)×4=96个,
当x=y=3时,正方形四个顶点为(3,3),(-3,3),(-3,-3),(3,-3),对角线分成4个区域中,正方形每边有7点,每个区域有七行,每行有4个点,4个区域中,每个区域有4×7=28个点,4个区域有(28-1)×4=108个,
当x=y=4时,正方形四个顶点为(4,4),(-4,4),(-4,-4),(4,-4),对角线分成4个区域中,正方形每边有9点,每个区域有九行,每行有3个点,4个区域中,每个区域有3×9=27个点,4个区域有(27-1)×4=104个,
当x=y=5时,正方形四个顶点为(5,5),(-5,5),(-5,-5),(5,-5),对角线分成4个区域中,正方形每边有11点,每个区域有十一行,每行有2个点,4个区域中,每个区域有2×11=22个点,4个区域有(22-1)×4=84个,
当x=y=6时,正方形四个顶点为(6,6),(-6,6),(-6,-6),(6,-6),对角线分成4个区域中,正方形每边有13点,每个区域有十三行,每行有1个点,4个区域中,每个区域有1×13=13个点,4个区域有(13-1)×4=48个,
∴n的最大值是108.
一、单选题
1.下列说法中,不正确的是( ).
A.在中,是的正比例函数
B.在中,是的正比例函数
C.在=3中,是的正比例函数
D.正方形的边长与周长为正比例关系
2.直线y=﹣2x+5与x轴、y轴的交点坐标分别是( )
A.(,0),(0,5) B.(﹣,0),(0,5)
C.(,0),(0,﹣5) D.(﹣,0),(0,﹣5)
3.点和点都在直线上,则与的关系是( )
A. B. C. D.
4.已知函数y=x+k+1是正比例函数,则k的值为( )
A.1 B.﹣1 C.0 D.±1
5.若函数是正比例函数,则下列叙述正确的是( )
A. B. C. D.y随x的增大而增大
6.已知是关于x的正比例函数,则m的值为( )
A.2 B.1 C.0或2 D.0
7.函数的图象与、y轴的交点为A、B,则AB等于 ( )
A. B.2 C.2 D.5
8.已知正比例函数y=(2m-1)x的图象上两点A(-1,y1),B(2,y2),且有y1>y2,那么m的取值范围是( )
A.m< B.m> C.m<2 D.m>2
9.在平面直角坐标系中,对于平面内一点(m,n)规定以下两种变换,
①f(m,n)=(m,–n),如f(2,1)=(2,–1);
②g(m,n)=(–m,–n),如g(2,1)=(–2,–1).
按照以上变换,则经过点f[g(3,4)],点g[f(–3,2)]的直线方程为()
A.y=–x+3 B.y=x+3 C.y=–x–3 D.y=x–3
10.如图,点C、B分别在两条直线y=﹣3x和y=kx上,点A、D是x轴上两点,若四边形ABCD是正方形,则k的值为( )
A.3 B.2 C. D.
二、填空题
11.已知正比例函数,y随x增大而减少,则k______0.
12.已知正比例函数中,y的值随x的增大而增大,则在第______象限.
13.一次函数y=kx+b的图象经过点(0,4),且与两坐标轴所围成的三角形的面积为8,则k=________,b=__________
14.已知一次函数,它的图象不经过第________象限.将直线向上平移个单位后,所得直线的表达式是________.
15.如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;
过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂
足为点A4…;这样一直作下去,则A2018的纵坐标为_____.
三、解答题
16.在同一直角坐标系中画出下列函数的图象:.
17.已知y﹣3与2x﹣1成正比例,且当x=1时,y=6.
(1)求y与x之间的函数解析式.
(2)当x=2时,求y的值.
(3)若点A(x1,y1),B(x2,y2)都在该函数的图象上,且y1>y2,试判断x1,x2的大小关系.
18.2017年12月29日郑州市人民政府通告:为减少机动车污染物排放,持续改善我市空气质量,从2018年1月1日起,每周工作日的7时至21时郑州市东三环、南三环、西三环、北三环以内区域的所有道路限行按机动车号牌(含临时号牌和外地号牌)最后一位阿拉伯数字(尾数为字母的以末尾数字为准),工作日每天限行2个号,即:号码最后一位阿拉伯数字为1和6的机动车周一限行,2和7的机动车周二限行,3和8的机动车周三限4和9的机动车周四限行,5和0的机动车周五限行,因法定节假日放假、调休而调整为上班的周六、周日按对应调体的工作日限行但通告中还规定,悬挂新能源专用牌的新能源汽车不受限制.限行通告发布后,新能源汽车成为畅销车型,某4S店销售每辆进价分别为5万元、9万元的A、B两种型号的新能源汽车,下表是近两周的销售情况:
(1)求A、B两种型号的新能源汽车的销售单价;(共
(2)若4S店准备用不超过200万元的金额采购这两种型号的新能源汽车共30辆,求B型号的新能源汽车最多能采购多少辆
(进价、售价均保持不变,利润=销售收入一进货成本)
(3在(2)的条件下,4S销售完这230辆新能源汽车时45店的最大利润是多少 并写
19.下表给出了一次函数y=kx+b(k≠0)中y与x的部分对应值.
x … -2 -1 5 …
y … 1 -1 -12 …
(1)根据表中的数据,确定一次函数的表达式;
(2)点(2,-5)是否在这个一次函数的图象上?请说明理由.
20.在平面直角坐标系中,对任意的点P(x,y),定义P的绝对坐标|P|=|x|+|y|.任取点A(x1,y1),B(x2,y2),记(x1,y2),(x2,y1),若此时|A|2+|B|2≤||2+||2成立,则称点A,B相关.
(1)分别判断下面各组中两点是相关点的是 ;
①A(﹣2,1),B(3,2);②C(4,﹣3),D(2,4).
(2)①对于点P(x,y),其中﹣6≤x≤6,﹣6≤y≤6,其中x,y是整数.则所有满足条件的P点有 个;
②求所有满足①条件的所有点中与点E(3,3)相关的点的个数;
③对于满足①条件的所有点中取出n个点,满足在这n个点中任意选择A,B两点,点A,B都相关,求n的最大值.
参考答案
1.A
2.A
3.A
4.B
5.C
6.D
7.B
8.A
9.A
10.D
11.<
12.一
13. ±1 4
14. 三, y=2x+1
15.
16.解:根据一次函数的特点,的图象过原点,且过点(1,2),
同理,的图象过原点,且过点(1,).
又由其图象为直线,作出图象如图所示.
17.解:(1)设y﹣3=k(2x﹣1),
把x=1,y=6代入得6﹣3=k(2×1﹣1),解得k=3,
则y﹣3=3(2x﹣1),
所以y与x之间的函数解析式为y=6x;
(2)由(1)知,y=6x
∴当x=2x时,y=6=12;
(3)∵,
而,
∴
∴
18.分析: (1)设A, B两种型号的新能源汽车的销售单价分别为x元,y元,根据表格中的等量关系可得 解得 ,(2) 设B型号的新能源汽车a辆,则采购A型号的新能源汽车 (30-a)辆,根据采购两种车辆的金额不超过200万元可列不等式
10a+5.8(30-a)≤200, 解得: a≤12.5,根据实际情况取整,
(3) 设4S店销售完这30辆车,获得的利润是万元,根据总利润=A型号的销售利润+B型号的销售利润,可得:,
详解:(1)设A, B两种型号的新能源汽车的销售单价分别为x元、y元,依题意得:
解得
答:A型汽车的销售单价为5.8万元,B型汽车的销售单价为10万元,
(2)设B型号的新能源汽车a辆,则采购A型号的新能源汽车 (30-a)辆,依题意得:
10a+5.8(30-a)≤200, 解得: a≤12.5. (a取整数),
答:4S店最多采购B型号的新能源汽车12辆.
(3)设4S店销售完这30辆车,获得的利润是万元,
,
,
w随a的增大而增大,
∴a最大时,w最大,
∵,且a是整数,
∴a=12时,w=24+0.2×12=26.4.
答:A型号采购18辆,B型号采购12辆时,利润最大,最大利润是26.4万元.
19.分析:(1)根据待定系数法求得即可;
(2)把点(2,﹣5)代入解析式即可判断.
详解:(1)根据题意得:,
解得:,所以一次函数的表达式为:y=﹣2x﹣3;
(2)点(2,﹣5)不在函数y=﹣2x﹣3的图象上.理由如下:
当x=2时,y=﹣2×2﹣3=﹣7≠﹣5,所以点(2,﹣5)不在函数y=﹣2x﹣3的图象上.
20.解:(1)①A(﹣2,1),B(3,2);A′(-2,2),B′(3,1),
∴,
∴;,
∵>,
∴①不是相关点,
②C(4,﹣3),D(2,4),,
,
∴;,
∵<,
∴②是相关点;
故答案为:②;
(2)①对于点P(x,y),其中﹣6≤x≤6,﹣6≤y≤6,其中x,y是整数.
∴x=-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,共13个整数,
∴y=-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,共13个整数,
所有满足条件的P(x,y)共有13×13=169个,
故答案为169;
②点E(3,3),设点Q(m,n)其中﹣6≤m≤6,﹣6≤n≤6,其中m,n是整数.
∵点E,Q是相关点,
∴,
整理得:,
因式分解得:,
∴或,
由得出两组解,
当时,
m=-3,-2,-1,0,1,2,3;n=-3,-4,-5,-6,7×4=28个;
当时,
m=-3,-2,-1,0,1,2,3;n=3,4,5,6,7×4=28个;
由,得出两组解,
当时,
m=-3,-4,-5,-6,n=-3,-2,-1,0,1,2,3;4×7=28个;
当时,
m=3,4,5,6,n=-3,-2,-1,0,1,2,3;4×7=28个;
(3,3)(3,-3)(-3,-3)(-3,3)各用两次,
所有与点E(3,3)相关的点的个数有4×28-4=108个,
故答案为108;
③设点A(x,y)其中﹣6≤x≤6,﹣6≤y≤6,其中x,y是整数,B(m,k)其中﹣6≤m≤6,﹣6≤k≤6,其中m,k是整数.
∵A、B是相关点,
∴,
整理得:,
因式分解得:,
或,
∴或,
∴或或或,
∴当x=y时,四点,组成正方形,由对角线y=x与y=-x,分成四个部分,每个部分中满足条件或或或是在每部分中长方形区域,在区域内都满足任意两点都是相关点,
每个区域中都有两个点在与上,当点P(x,y),
当x=y=0时,为坐标轴上点,4个区域中,每个区域有7个点,4各区域有(7-1)×4+1=25个,
当x=y=1时,正方形四个顶点为(1,1),(-1,1),(-1,-1),(1,-1),对角线分成4个区域中,正方形每边有3点,每个区域有三行,每行有6个点,每个区域有6×3=18个点,4个区域有(18-1)×4=68个,
当x=y=2时,正方形四个顶点为(2,2),(-2,2),(-2,-2),(2,-2),对角线分成4个区域中,正方形每边有5点,每个区域有五行,每行有5个点,4个区域中,每个区域有5×5=25个点,4个区域有(25-1)×4=96个,
当x=y=3时,正方形四个顶点为(3,3),(-3,3),(-3,-3),(3,-3),对角线分成4个区域中,正方形每边有7点,每个区域有七行,每行有4个点,4个区域中,每个区域有4×7=28个点,4个区域有(28-1)×4=108个,
当x=y=4时,正方形四个顶点为(4,4),(-4,4),(-4,-4),(4,-4),对角线分成4个区域中,正方形每边有9点,每个区域有九行,每行有3个点,4个区域中,每个区域有3×9=27个点,4个区域有(27-1)×4=104个,
当x=y=5时,正方形四个顶点为(5,5),(-5,5),(-5,-5),(5,-5),对角线分成4个区域中,正方形每边有11点,每个区域有十一行,每行有2个点,4个区域中,每个区域有2×11=22个点,4个区域有(22-1)×4=84个,
当x=y=6时,正方形四个顶点为(6,6),(-6,6),(-6,-6),(6,-6),对角线分成4个区域中,正方形每边有13点,每个区域有十三行,每行有1个点,4个区域中,每个区域有1×13=13个点,4个区域有(13-1)×4=48个,
∴n的最大值是108.
