人教版八年级下册 19.2.2一次函数巩固培优练 含答案
文档属性
| 名称 | 人教版八年级下册 19.2.2一次函数巩固培优练 含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 422.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 22:01:18 | ||
图片预览


文档简介
19.2.2一次函数 巩固培优练
一、单选题
1.一次函数的图象大致是( )
A. B.
C. D.
2.若直线不经过第三象限,则的值可以为( )
A. B. C. D.
3.对于一次函数,为常数),如表中给出几组自变量及其对应的函数值,其中恰好有一个函数值计算有误,则这个错误的函数值是( )
0 1 3
7 5 2
A. B.2 C.5 D.7
4.直线与轴的交点坐标是( )
A. B. C. D.
5.在平面直角坐标系xOy中,A(1,3),B(5,1),点M在x轴上,当MA+MB取得最小值时,点M的坐标为( )
A.(5,0) B.(4,0) C.(1,0) D.(0,4)
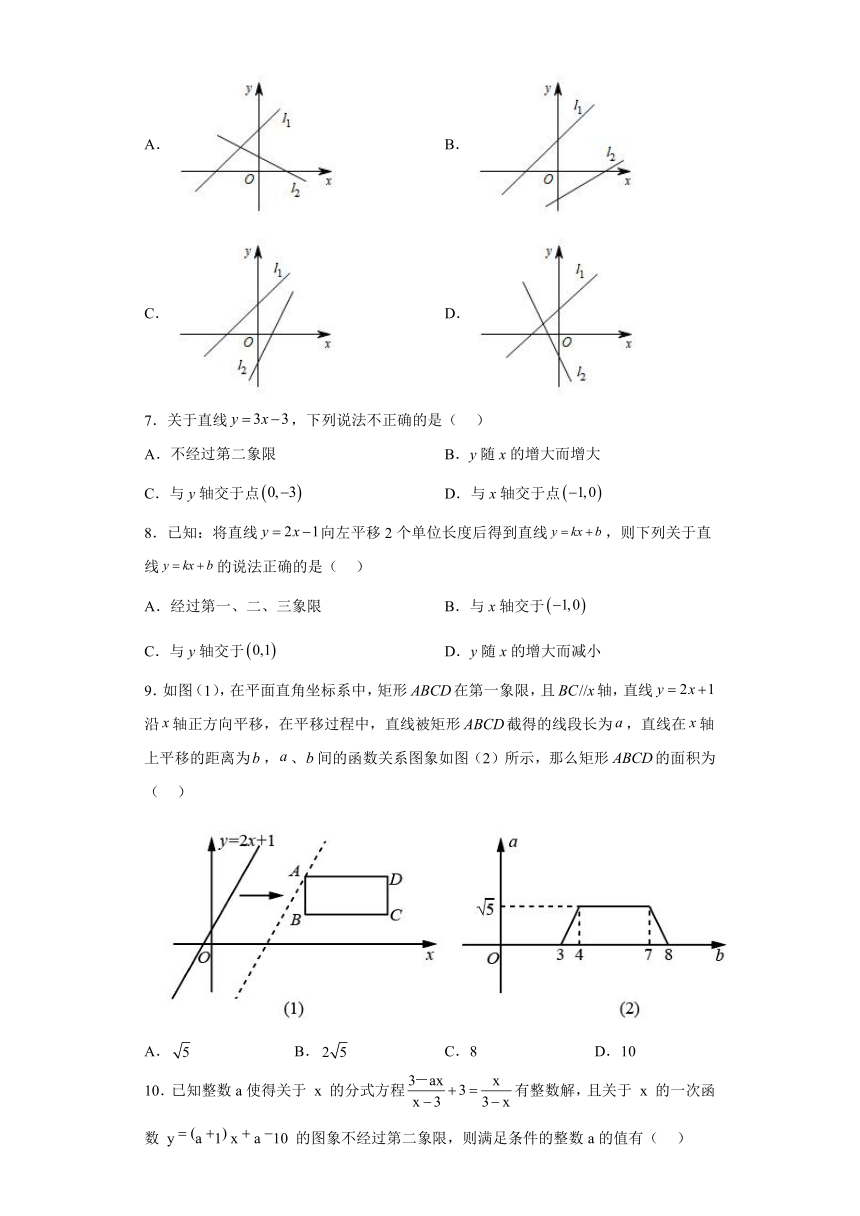
6.直线和在同一直角坐标系中的图象可能是( )
A. B.
C. D.
7.关于直线,下列说法不正确的是( )
A.不经过第二象限 B.y随x的增大而增大
C.与y轴交于点 D.与x轴交于点
8.已知:将直线向左平移2个单位长度后得到直线,则下列关于直线的说法正确的是( )
A.经过第一、二、三象限 B.与x轴交于
C.与y轴交于 D.y随x的增大而减小
9.如图(1),在平面直角坐标系中,矩形在第一象限,且轴,直线沿轴正方向平移,在平移过程中,直线被矩形截得的线段长为,直线在轴上平移的距离为,、间的函数关系图象如图(2)所示,那么矩形的面积为( )
A. B. C.8 D.10
10.已知整数a使得关于 x 的分式方程有整数解,且关于 x 的一次函数 y a 1 x a 10 的图象不经过第二象限,则满足条件的整数a的值有( )
A.6 个 B.5个 C.4 个 D.3个
二、填空题
11.设点(1,a)和点(-2,b)是直线y=(1-k2)x+3(012.已知一次函数y=﹣x+k的图象经过A(a,﹣1),B(b,﹣2)两点,则a_____b(填“>”“<”或“=”).
13.已知一次函数(m为常数),若其图象经过第一、三、四象限,则m的取值范围为____.
14.已知,在平面直角坐标系xOy中,A(1,0),B(0,2),点C是x轴上一点,且满足∠ABC = 45°,则点C的坐标是 _________
15.如图,已知直线y=x+6与x轴,y轴相交于点A,B,点C在线段OA上,将△BOC沿着BC折叠后,点O恰好落在AB边上的点D处,若点P为平面内异于点C的一点,且满足△ABC与△ABP全等,则点P的坐标为_____.
三、解答题
16.已知一次函数图象过点(1,4)和(0,2),求这个一次函数的解析式,并在直角坐标系中画出该函数图象.
17.已知直线y=kx+b(k≠0)经过点A(3,0),B(1,2)
(1)求直线y=kx+b的函数表达式;
(2)若直线y=x﹣2与直线y=kx+b相交于点C,求点C的坐标;
(3)写出不等式kx+b>x﹣2的解.
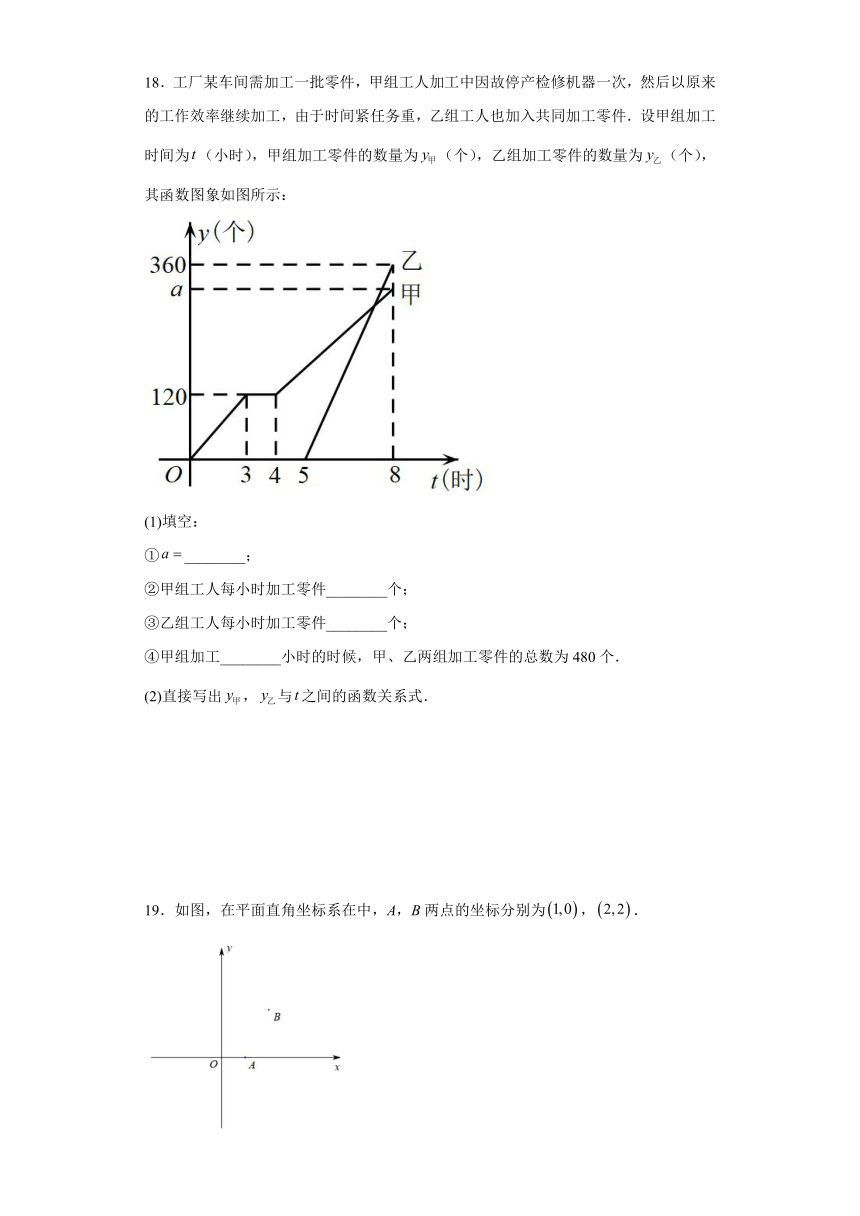
18.工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间为(小时),甲组加工零件的数量为(个),乙组加工零件的数量为(个),其函数图象如图所示:
(1)填空:
①________;
②甲组工人每小时加工零件________个;
③乙组工人每小时加工零件________个;
④甲组加工________小时的时候,甲、乙两组加工零件的总数为480个.
(2)直接写出,与之间的函数关系式.
19.如图,在平面直角坐标系在中,A,B两点的坐标分别为,.
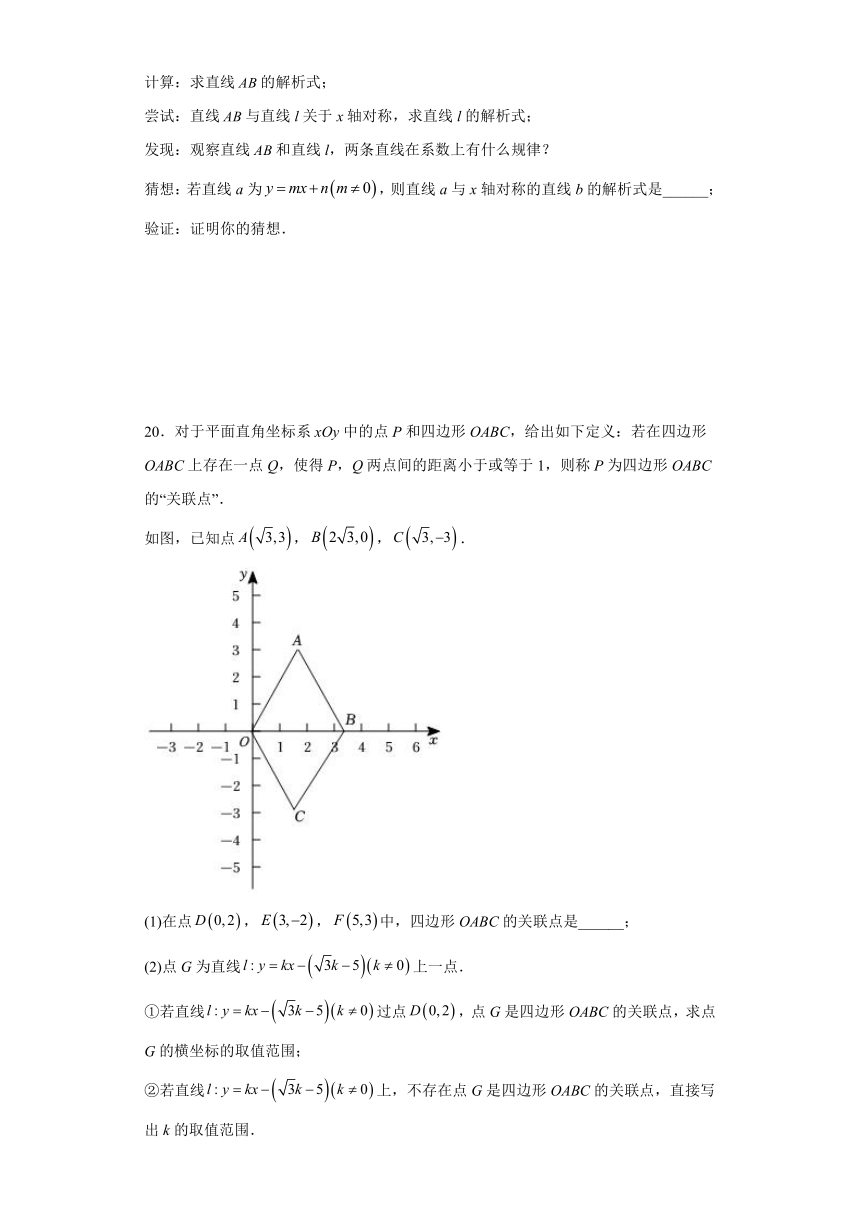
计算:求直线的解析式;
尝试:直线与直线l关于x轴对称,求直线l的解析式;
发现:观察直线和直线l,两条直线在系数上有什么规律?
猜想:若直线a为,则直线a与x轴对称的直线b的解析式是______;
验证:证明你的猜想.
20.对于平面直角坐标系xOy中的点P和四边形OABC,给出如下定义:若在四边形OABC上存在一点Q,使得P,Q两点间的距离小于或等于1,则称P为四边形OABC的“关联点”.
如图,已知点,,.
(1)在点,,中,四边形OABC的关联点是______;
(2)点G为直线上一点.
①若直线过点,点G是四边形OABC的关联点,求点G的横坐标的取值范围;
②若直线上,不存在点G是四边形OABC的关联点,直接写出k的取值范围.
参考答案
1.A
2.A
3.B
4.C
5.B
6.D
7.D
8.A
9.C
10.A
11.a>b
12.<
13.
14.或/或
15.(﹣,)或(﹣5,6)或(﹣,)
16.解:设一次函数解析式为y=kx+b,
将(1,4)和(0,2)代入y=kx+b,得
解得,
∴一次函数解析式为y=2x+2,
如图,
17.解:(1)根据题意得,解得,
∴直线解析式为y=﹣x+3;
(2)解方程组得,
∴C点坐标为(,);
(3)解不等式﹣x+3>x﹣2得x<,
即不等式kx+b>x﹣2的解集为x<.
18. (1)解:①甲组工人的工作效率为(个/小时),
则,
解得,
故答案为:280;
②甲组工人每小时加工零件的个数为(个),
故答案为:40;
③乙组工人每小时加工零件的个数为(个),
故答案为:120;
④因为在乙组工人加入之前,甲组工人加工的零件个数为,
所以当甲、乙两组加工零件的总数为480个时,,
则,
解得,
即甲组加工7小时的时候,甲、乙两组加工零件的总数为480个,
故答案为:7.
(2)
解:当时,,
当时,,
当时,设,
将点代入得:,解得,
则此时,
综上,;
当时,设,
将点代入得:,解得,
则.
19.解:计算:设直线AB的解析式为y=kx+b,过A,B两点,
代入得
②-①得,
把代入①得.
∴
直线AB的解析式为y=2x-2;
尝试:直线与直线l关于x轴对称,
点A在x轴上,点B的对称点为B′(2,-2)
直线l的解析式为y=px+q,过A,B′两点
代入得
解得
∴直线l的解析式为y=-2x+2;
发现:观察直线和直线l关于x轴对称,两条直线的一次项系数互为相反数,常数项也互为相反数;
猜想:若直线a为,则直线a与x轴对称的直线b的解析式是_y=-mx-n;
故答案为y=-mx-n;
证明:直线a为,x=0,y=n,y轴上点为(0,n),当y=0时,,解得
x轴上点为(,0)
点(0,n)关于x轴对称点为(0,-n),
过点(,0)与(0,-n)两点的解析式为y=cx+d,
代入得
解得
∴y=-mx-n.
20. (1)解:如下图所示,过点A作轴,垂足为M;过点D作,垂足为N;
过点F作垂足为H,过点F作轴,垂足为K,过点H作轴,B并交于点J;
过点E作垂足为G,过点C作轴,过点B作轴,、交于点P,过点E做轴,交于点L;
由题意得,,,,
∴;,
∴,
∴,
∴,
∵,
∴点D是四边形OABC的关联点,
∵,,,,
∴,
∴,
∴,
∴,
∵,
∴,
∴点E是四边形OABC的关联点;
∵,
∴
∵
∴点F是四边不是形OABC的关联点;
故答案为:D,E;
(2)
①∵直线过点,
∴,得.
∴直线,
∴直线与x轴的交点.
∵,
∴直线OA的解析式是,
∴,
分别过点O,点A作直线l的垂线,垂足分别为E,F,
∴,
∴四边形OAFE是平行四边形,
∵,
∴,
∴平行四边形OAFE是矩形,
∴,
∵,,
∴,
∴是等边三角形,
∴,
∴.
∵,
∴,
∴,
∴由平移可知.
∵点G是四边形OABC的关联点,
∴点G在线段EF上,
∴,
②∵,
∴直线OC的解析式是,
如下图所示,将直线OC沿着垂直OC的方向向下平移1得到直线,
在直线与的夹角范围外,不存在四边形OABC的关联点,
∴或.
一、单选题
1.一次函数的图象大致是( )
A. B.
C. D.
2.若直线不经过第三象限,则的值可以为( )
A. B. C. D.
3.对于一次函数,为常数),如表中给出几组自变量及其对应的函数值,其中恰好有一个函数值计算有误,则这个错误的函数值是( )
0 1 3
7 5 2
A. B.2 C.5 D.7
4.直线与轴的交点坐标是( )
A. B. C. D.
5.在平面直角坐标系xOy中,A(1,3),B(5,1),点M在x轴上,当MA+MB取得最小值时,点M的坐标为( )
A.(5,0) B.(4,0) C.(1,0) D.(0,4)
6.直线和在同一直角坐标系中的图象可能是( )
A. B.
C. D.
7.关于直线,下列说法不正确的是( )
A.不经过第二象限 B.y随x的增大而增大
C.与y轴交于点 D.与x轴交于点
8.已知:将直线向左平移2个单位长度后得到直线,则下列关于直线的说法正确的是( )
A.经过第一、二、三象限 B.与x轴交于
C.与y轴交于 D.y随x的增大而减小
9.如图(1),在平面直角坐标系中,矩形在第一象限,且轴,直线沿轴正方向平移,在平移过程中,直线被矩形截得的线段长为,直线在轴上平移的距离为,、间的函数关系图象如图(2)所示,那么矩形的面积为( )
A. B. C.8 D.10
10.已知整数a使得关于 x 的分式方程有整数解,且关于 x 的一次函数 y a 1 x a 10 的图象不经过第二象限,则满足条件的整数a的值有( )
A.6 个 B.5个 C.4 个 D.3个
二、填空题
11.设点(1,a)和点(-2,b)是直线y=(1-k2)x+3(0
13.已知一次函数(m为常数),若其图象经过第一、三、四象限,则m的取值范围为____.
14.已知,在平面直角坐标系xOy中,A(1,0),B(0,2),点C是x轴上一点,且满足∠ABC = 45°,则点C的坐标是 _________
15.如图,已知直线y=x+6与x轴,y轴相交于点A,B,点C在线段OA上,将△BOC沿着BC折叠后,点O恰好落在AB边上的点D处,若点P为平面内异于点C的一点,且满足△ABC与△ABP全等,则点P的坐标为_____.
三、解答题
16.已知一次函数图象过点(1,4)和(0,2),求这个一次函数的解析式,并在直角坐标系中画出该函数图象.
17.已知直线y=kx+b(k≠0)经过点A(3,0),B(1,2)
(1)求直线y=kx+b的函数表达式;
(2)若直线y=x﹣2与直线y=kx+b相交于点C,求点C的坐标;
(3)写出不等式kx+b>x﹣2的解.
18.工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间为(小时),甲组加工零件的数量为(个),乙组加工零件的数量为(个),其函数图象如图所示:
(1)填空:
①________;
②甲组工人每小时加工零件________个;
③乙组工人每小时加工零件________个;
④甲组加工________小时的时候,甲、乙两组加工零件的总数为480个.
(2)直接写出,与之间的函数关系式.
19.如图,在平面直角坐标系在中,A,B两点的坐标分别为,.
计算:求直线的解析式;
尝试:直线与直线l关于x轴对称,求直线l的解析式;
发现:观察直线和直线l,两条直线在系数上有什么规律?
猜想:若直线a为,则直线a与x轴对称的直线b的解析式是______;
验证:证明你的猜想.
20.对于平面直角坐标系xOy中的点P和四边形OABC,给出如下定义:若在四边形OABC上存在一点Q,使得P,Q两点间的距离小于或等于1,则称P为四边形OABC的“关联点”.
如图,已知点,,.
(1)在点,,中,四边形OABC的关联点是______;
(2)点G为直线上一点.
①若直线过点,点G是四边形OABC的关联点,求点G的横坐标的取值范围;
②若直线上,不存在点G是四边形OABC的关联点,直接写出k的取值范围.
参考答案
1.A
2.A
3.B
4.C
5.B
6.D
7.D
8.A
9.C
10.A
11.a>b
12.<
13.
14.或/或
15.(﹣,)或(﹣5,6)或(﹣,)
16.解:设一次函数解析式为y=kx+b,
将(1,4)和(0,2)代入y=kx+b,得
解得,
∴一次函数解析式为y=2x+2,
如图,
17.解:(1)根据题意得,解得,
∴直线解析式为y=﹣x+3;
(2)解方程组得,
∴C点坐标为(,);
(3)解不等式﹣x+3>x﹣2得x<,
即不等式kx+b>x﹣2的解集为x<.
18. (1)解:①甲组工人的工作效率为(个/小时),
则,
解得,
故答案为:280;
②甲组工人每小时加工零件的个数为(个),
故答案为:40;
③乙组工人每小时加工零件的个数为(个),
故答案为:120;
④因为在乙组工人加入之前,甲组工人加工的零件个数为,
所以当甲、乙两组加工零件的总数为480个时,,
则,
解得,
即甲组加工7小时的时候,甲、乙两组加工零件的总数为480个,
故答案为:7.
(2)
解:当时,,
当时,,
当时,设,
将点代入得:,解得,
则此时,
综上,;
当时,设,
将点代入得:,解得,
则.
19.解:计算:设直线AB的解析式为y=kx+b,过A,B两点,
代入得
②-①得,
把代入①得.
∴
直线AB的解析式为y=2x-2;
尝试:直线与直线l关于x轴对称,
点A在x轴上,点B的对称点为B′(2,-2)
直线l的解析式为y=px+q,过A,B′两点
代入得
解得
∴直线l的解析式为y=-2x+2;
发现:观察直线和直线l关于x轴对称,两条直线的一次项系数互为相反数,常数项也互为相反数;
猜想:若直线a为,则直线a与x轴对称的直线b的解析式是_y=-mx-n;
故答案为y=-mx-n;
证明:直线a为,x=0,y=n,y轴上点为(0,n),当y=0时,,解得
x轴上点为(,0)
点(0,n)关于x轴对称点为(0,-n),
过点(,0)与(0,-n)两点的解析式为y=cx+d,
代入得
解得
∴y=-mx-n.
20. (1)解:如下图所示,过点A作轴,垂足为M;过点D作,垂足为N;
过点F作垂足为H,过点F作轴,垂足为K,过点H作轴,B并交于点J;
过点E作垂足为G,过点C作轴,过点B作轴,、交于点P,过点E做轴,交于点L;
由题意得,,,,
∴;,
∴,
∴,
∴,
∵,
∴点D是四边形OABC的关联点,
∵,,,,
∴,
∴,
∴,
∴,
∵,
∴,
∴点E是四边形OABC的关联点;
∵,
∴
∵
∴点F是四边不是形OABC的关联点;
故答案为:D,E;
(2)
①∵直线过点,
∴,得.
∴直线,
∴直线与x轴的交点.
∵,
∴直线OA的解析式是,
∴,
分别过点O,点A作直线l的垂线,垂足分别为E,F,
∴,
∴四边形OAFE是平行四边形,
∵,
∴,
∴平行四边形OAFE是矩形,
∴,
∵,,
∴,
∴是等边三角形,
∴,
∴.
∵,
∴,
∴,
∴由平移可知.
∵点G是四边形OABC的关联点,
∴点G在线段EF上,
∴,
②∵,
∴直线OC的解析式是,
如下图所示,将直线OC沿着垂直OC的方向向下平移1得到直线,
在直线与的夹角范围外,不存在四边形OABC的关联点,
∴或.
