19.2.3一次函数与方程、不等式巩固培优练(含答案)数学人教版八年级下册
文档属性
| 名称 | 19.2.3一次函数与方程、不等式巩固培优练(含答案)数学人教版八年级下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 410.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 22:01:27 | ||
图片预览



文档简介
19.2.3一次函数与方程、不等式 巩固培优练
一、单选题
1.如图,一次函数的图象交轴于点,则不等式的解集为( )
A. B. C. D.
2.若一次函数与的图像相交于点,则关于,的二元一次方程组的解是( )
A. B. C. D.
3.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
4.如图,正比例函数y=kx(k是常数,k≠0)的图象与一次函数y=x+1的图象相交于点P,点P的纵坐标是2,则不等式kx<x+1的解集是( )
A.x<1 B.x>1 C.x>2 D.x<2
5.一次函数y=mx+n的图象如图所示,则方程mx+n=0的解为( )
A.x=2 B.y=2 C.x=-3 D.y=-3
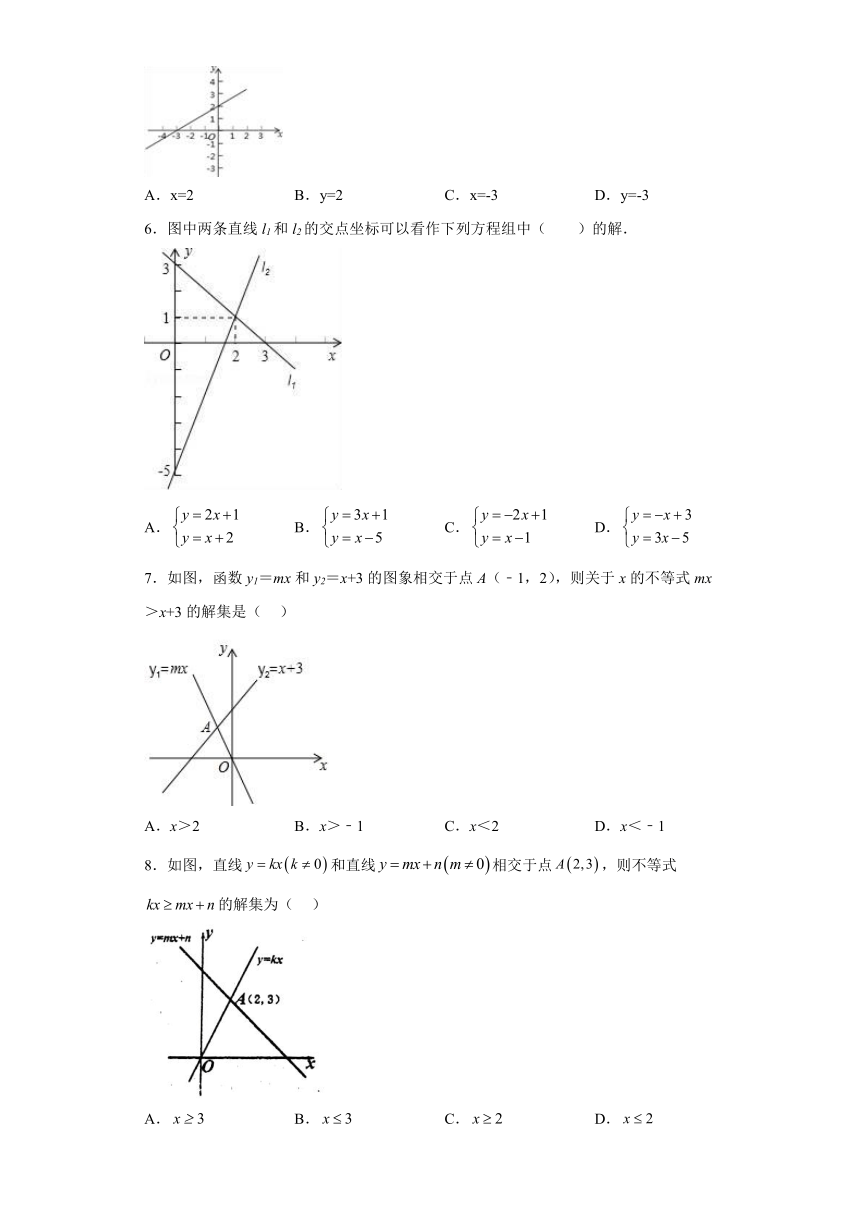
6.图中两条直线l1和l2的交点坐标可以看作下列方程组中( )的解.
A. B. C. D.
7.如图,函数y1=mx和y2=x+3的图象相交于点A(﹣1,2),则关于x的不等式mx>x+3的解集是( )
A.x>2 B.x>﹣1 C.x<2 D.x<﹣1
8.如图,直线和直线相交于点,则不等式的解集为( )
A. B. C. D.
9.已知直线y=﹣x+2与直线y=2x+6相交于点A,与x轴分别交于B,C两点,若点D(a,a+1)落在△ABC内部(不含边界),则a的取值范围是( )
A.﹣3<a<2 B. C. D.﹣2<a<2
10.直线y=px(p是不等于0的整数)与直线y=x+10的交点恰好是整点(横坐标和纵坐标都是整数),那么满足条件的直线有( )
A.6条 B.7条 C.8条 D.无数条
二、填空题
11.方程组的解为,则一次函数和图象的交点坐标为______.
12.直线与直线相交于点M(1,2),则关于x,y的方程组的解为____________.
13.如图,函数y=2x和y=ax+4的图象相交于点A(,3),则不等式2x>ax+4的解集为___.
14.如图,直线与的交点的坐标为5,则关于x的不等式组的解集是______.
15.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是_____.
三、解答题
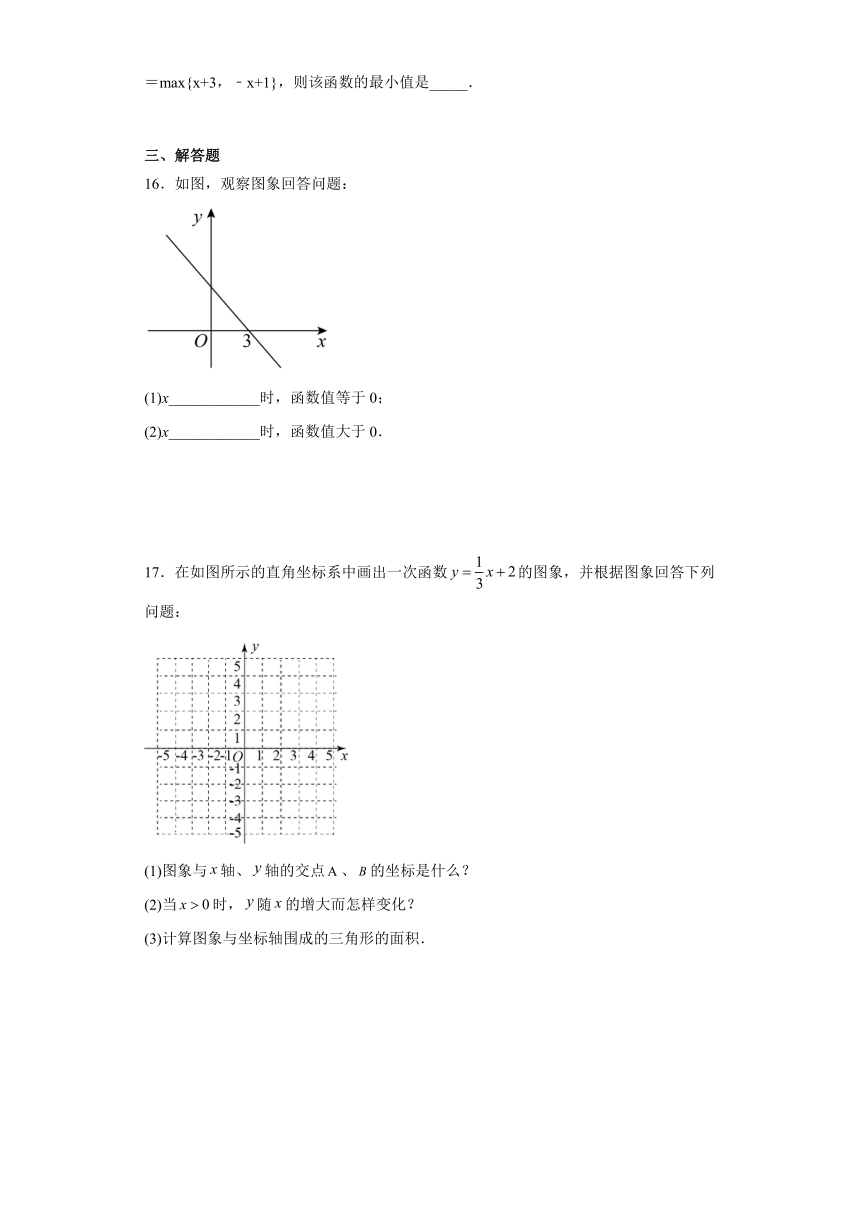
16.如图,观察图象回答问题:
(1)x____________时,函数值等于0;
(2)x____________时,函数值大于0.
17.在如图所示的直角坐标系中画出一次函数的图象,并根据图象回答下列问题:
(1)图象与轴、轴的交点、的坐标是什么?
(2)当时,随的增大而怎样变化?
(3)计算图象与坐标轴围成的三角形的面积.
18.如图,在平面直角坐标系中,过点的直线与直线相交于点,动点沿路线运动.
(1)求直线的解析式.
(2)求的面积.
(3)当的面积是的面积的时,求出这时点的坐标.
19.已知两直线与
(1)在同一平面直角坐标系中作出两直线的图象;
(2)求出两直线的交点;
(3)根据图象指出x为何值时,;
(4)求这两条直线与x轴围成的三角形面积.
20.已知:如图,一次函数的图象与反比例函数的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
(1)直接写出M、N的坐标及k的值;
(2)将线段CP绕点P按逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出点Q的坐标;如果不能,请说明理由;
(3)当点P滑动时,是否存在反比例函数图象(第一象限的一支)上的点S,使得以P、S、M、N四个点为顶点的四边形是平行四边形?若存在,请直接写出所有符合题意的点S的坐标;若不存在,请说明理由.
参考答案
1.C
2.B
3.A
4.A
5.C
6.D
7.D
8.C
9.B
10.B
11.
12.
13.x>
14.
15.2
16.(1)解:函数与x轴的交点坐标为(3,0),且y随x的增大而减小.
∴当x=3时,函数值等于0;
故答案为:=3;
(2)解:函数与x轴的交点坐标为(3,0),且y随x的增大而减小.
∴当x<3时,函数值大于0.
故答案为:<3;
17.(1)解:直线与轴的交点纵坐标为0,与轴的交点横坐标为0,
当时,,解得,
当时,,
所以直线与轴的交点、与轴的交点为,描点连线画出函数图像;
(2)由图象可得,当时,随的增大而增大;
(3),即图象与坐标轴围成的三角形的面积为6.
18. (1)设直线的解析式为,
由题意,将点代入得:,
解得,
则直线的解析式为.
(2)解:对于函数,
当时,,即,
,
的边上的高为3,
则的面积为.
(3)解:设直线的解析式为,
将点代入得:,解得,
则直线的解析式为,
由题意,分以下两种情况:
①如图,当点在线段上时,
设点的坐标为,
的面积是的面积的,且的面积为6,
,
解得,
则,
所以此时点的坐标为;
②如图,当点在线段上时,
设点的坐标为,
的面积是的面积的,且的面积为6,
,
解得,
则,
所以此时点的坐标为;
综上,点的坐标为或.
19解:(1)如图所示:
(2)由,得,∴两直线的交点坐标为(2,3);
(3)由函数图象知,当x<2时,的图象在图象的上方,
∴当x<2时,y1>y2;
(4)∵两直线与x轴的交点坐标分别为(,0),(5,0),交点坐标为(2,3),
∴这两条直线与x轴围成的三角形面积为:×(5)×3=.
20.解:(1)当时,,.
当时,,解得,
将点代入得,
;
(2)若CP逆时针旋转,点Q在双曲线上,
设,则,
,即,
,
;
(3)设,
当MN为平行四边形的一条边时,则,
把S点的坐标代入,得,解得.
当MN为平行四边形的对角线时,则,
把S点的坐标代入,得,解得,
∴存在,S的坐标为或.
一、单选题
1.如图,一次函数的图象交轴于点,则不等式的解集为( )
A. B. C. D.
2.若一次函数与的图像相交于点,则关于,的二元一次方程组的解是( )
A. B. C. D.
3.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
4.如图,正比例函数y=kx(k是常数,k≠0)的图象与一次函数y=x+1的图象相交于点P,点P的纵坐标是2,则不等式kx<x+1的解集是( )
A.x<1 B.x>1 C.x>2 D.x<2
5.一次函数y=mx+n的图象如图所示,则方程mx+n=0的解为( )
A.x=2 B.y=2 C.x=-3 D.y=-3
6.图中两条直线l1和l2的交点坐标可以看作下列方程组中( )的解.
A. B. C. D.
7.如图,函数y1=mx和y2=x+3的图象相交于点A(﹣1,2),则关于x的不等式mx>x+3的解集是( )
A.x>2 B.x>﹣1 C.x<2 D.x<﹣1
8.如图,直线和直线相交于点,则不等式的解集为( )
A. B. C. D.
9.已知直线y=﹣x+2与直线y=2x+6相交于点A,与x轴分别交于B,C两点,若点D(a,a+1)落在△ABC内部(不含边界),则a的取值范围是( )
A.﹣3<a<2 B. C. D.﹣2<a<2
10.直线y=px(p是不等于0的整数)与直线y=x+10的交点恰好是整点(横坐标和纵坐标都是整数),那么满足条件的直线有( )
A.6条 B.7条 C.8条 D.无数条
二、填空题
11.方程组的解为,则一次函数和图象的交点坐标为______.
12.直线与直线相交于点M(1,2),则关于x,y的方程组的解为____________.
13.如图,函数y=2x和y=ax+4的图象相交于点A(,3),则不等式2x>ax+4的解集为___.
14.如图,直线与的交点的坐标为5,则关于x的不等式组的解集是______.
15.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是_____.
三、解答题
16.如图,观察图象回答问题:
(1)x____________时,函数值等于0;
(2)x____________时,函数值大于0.
17.在如图所示的直角坐标系中画出一次函数的图象,并根据图象回答下列问题:
(1)图象与轴、轴的交点、的坐标是什么?
(2)当时,随的增大而怎样变化?
(3)计算图象与坐标轴围成的三角形的面积.
18.如图,在平面直角坐标系中,过点的直线与直线相交于点,动点沿路线运动.
(1)求直线的解析式.
(2)求的面积.
(3)当的面积是的面积的时,求出这时点的坐标.
19.已知两直线与
(1)在同一平面直角坐标系中作出两直线的图象;
(2)求出两直线的交点;
(3)根据图象指出x为何值时,;
(4)求这两条直线与x轴围成的三角形面积.
20.已知:如图,一次函数的图象与反比例函数的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
(1)直接写出M、N的坐标及k的值;
(2)将线段CP绕点P按逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出点Q的坐标;如果不能,请说明理由;
(3)当点P滑动时,是否存在反比例函数图象(第一象限的一支)上的点S,使得以P、S、M、N四个点为顶点的四边形是平行四边形?若存在,请直接写出所有符合题意的点S的坐标;若不存在,请说明理由.
参考答案
1.C
2.B
3.A
4.A
5.C
6.D
7.D
8.C
9.B
10.B
11.
12.
13.x>
14.
15.2
16.(1)解:函数与x轴的交点坐标为(3,0),且y随x的增大而减小.
∴当x=3时,函数值等于0;
故答案为:=3;
(2)解:函数与x轴的交点坐标为(3,0),且y随x的增大而减小.
∴当x<3时,函数值大于0.
故答案为:<3;
17.(1)解:直线与轴的交点纵坐标为0,与轴的交点横坐标为0,
当时,,解得,
当时,,
所以直线与轴的交点、与轴的交点为,描点连线画出函数图像;
(2)由图象可得,当时,随的增大而增大;
(3),即图象与坐标轴围成的三角形的面积为6.
18. (1)设直线的解析式为,
由题意,将点代入得:,
解得,
则直线的解析式为.
(2)解:对于函数,
当时,,即,
,
的边上的高为3,
则的面积为.
(3)解:设直线的解析式为,
将点代入得:,解得,
则直线的解析式为,
由题意,分以下两种情况:
①如图,当点在线段上时,
设点的坐标为,
的面积是的面积的,且的面积为6,
,
解得,
则,
所以此时点的坐标为;
②如图,当点在线段上时,
设点的坐标为,
的面积是的面积的,且的面积为6,
,
解得,
则,
所以此时点的坐标为;
综上,点的坐标为或.
19解:(1)如图所示:
(2)由,得,∴两直线的交点坐标为(2,3);
(3)由函数图象知,当x<2时,的图象在图象的上方,
∴当x<2时,y1>y2;
(4)∵两直线与x轴的交点坐标分别为(,0),(5,0),交点坐标为(2,3),
∴这两条直线与x轴围成的三角形面积为:×(5)×3=.
20.解:(1)当时,,.
当时,,解得,
将点代入得,
;
(2)若CP逆时针旋转,点Q在双曲线上,
设,则,
,即,
,
;
(3)设,
当MN为平行四边形的一条边时,则,
把S点的坐标代入,得,解得.
当MN为平行四边形的对角线时,则,
把S点的坐标代入,得,解得,
∴存在,S的坐标为或.
