9.3.2 用多种正多边形铺设地面 课件(共26张PPT)
文档属性
| 名称 | 9.3.2 用多种正多边形铺设地面 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
9.3.2用多种正多边形铺设地面
华师大版 七年级 下册
教学目标
教学目标:1.使学生理解多种正多边形能够铺满地面的数学道理,掌握两
种及两种以上的正多边形能够铺满地面的种类.
2.通过“拼地板”和相关计算,使学生从中发现能拼成一个不
留空隙,又不重叠的平面图形的关键是几个多边形的内角和
相加要等于360°.
教学重点:通过用两种以上正多边形拼地板,提高学生观察、分析、概括、
抽象能力.
教学难点:寻找用哪几种正多边形能铺满地板的种类.
新知导入
情境引入
问题1
能用同一种正多边形铺满地板的都有谁?说一说,并从下图中找出
只有正三角形,正四边形,正六边形可以铺满地板.
新知讲解
合作学习
用相同的任意三角形、任意四边形能密铺吗?
思考
请各位同学以小组为单位随意剪出一些形状、大小都一样的四边形,拼拼看,能否铺满地面.
这是为什么呢?
小结:不规则四边形能用来铺地板的道理是:“任意四边形(指凸四边形)内角之和都等于360°。”因此,不管切下的四边形怎样歪七扭八,只要形状完全相同,4块相拼就能凑成360°,而且总能找到等长的边相接,使砖与砖之间不留缝隙.
结论:形状、大小相同的任意四边形能镶嵌成平面图形.
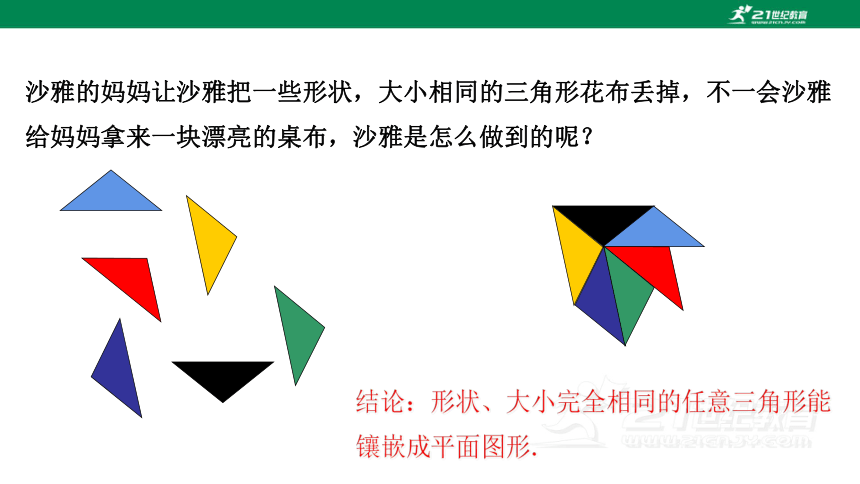
沙雅的妈妈让沙雅把一些形状,大小相同的三角形花布丢掉,不一会沙雅给妈妈拿来一块漂亮的桌布,沙雅是怎么做到的呢?
结论:形状、大小完全相同的任意三角形能镶嵌成平面图形.
规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.
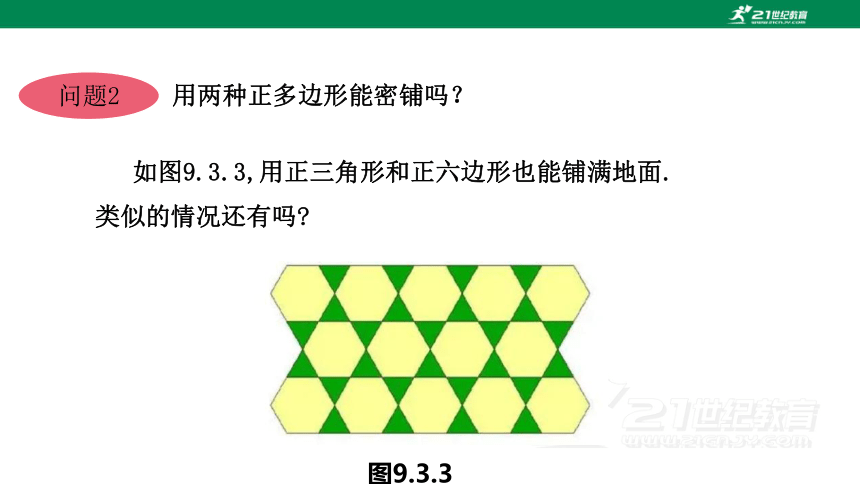
用两种正多边形能密铺吗?
问题2
如图9.3.3,用正三角形和正六边形也能铺满地面.类似的情况还有吗
图9.3.3
1.正八边形和正方形组合.
135°+135°+90°=360°
正八边形的每一内角度数是135°,而正四边形的每一个内角是90°。两个135°与1个90°的和刚好是360°,
2.正十二边形和正三角形组合
150°+150°+60°=360°
正十二边形的每一内角度数是150°,而正三角形的每一个内角是60°。两个150°与1个60°的和刚好也是360°。
规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.
用三种正多边形能密铺吗?
问题3
90°
120°
150°
150°+120°+90°=360°
提炼概念
其他的图形是否也满足这一条件
当围绕一点拼在一起的几个多边形的内角和恰好组成一个周角时,就能铺满地面。
典例精讲
能扩展到整个平面,即铺满地面吗?
144°+108°+108°=360°
144°
108°
108°
例:正五边形、正十边形铺设地面
正五边形、正十边形铺设地面不能扩展到整个平面。
归纳概念
易错点:
有时几种正多边形的组合虽然能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面。
如正五边形和正十边形的组合。
或满足:
内角度数×m + 另一种内角度数×n+第三种内角度数×k =360°
的方程正整数解.
规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角(360°)时,就能铺满地面。
课堂练习
1.只用下列正多边形,能铺满地面的是( )
A.正五边形 B.正八边形 C.正六边形 D.正十边形
C
2.某中学新科技馆铺设地面,已有正三角形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则该学校不应该购买的地砖形状是( )
A.正方形 B.正六边形 C.正八边形 D.正十二边形
C
3、如图,是正在铺设的人行道上地板砖的部分,是由正六边形和四边形镶嵌而成的图形,则图中的四边形中的锐角∠BAD的度数是______度.
60
4、用正三角形和正六边形材料铺地面,在一个顶点周围有几个正三角形和几个正六边形?说明你的理由.
答:在一个顶点周围有4个正三角形和1个正六边形
或者在一个顶点周围有2个正三角形和2个正六边形
解:设在一个顶点周围有m个正三角形的角,n个正六边形的角。
由题意得 m×60°+ n×120°= 360°
即m+ 2n= 6 满足题意的正整数解为
m=4
n=1
m=2
n=2
或
课堂总结
用多种正多边形铺设地面
当围绕一点拼在一起的几个多边形的内角和恰好组成一个周角时,就能铺满地面。
有时几种正多边形的组合虽然能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面。
如正五边形和正十边形的组合。
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
9.3.2用多种正多边形铺设地面
华师大版 七年级 下册
教学目标
教学目标:1.使学生理解多种正多边形能够铺满地面的数学道理,掌握两
种及两种以上的正多边形能够铺满地面的种类.
2.通过“拼地板”和相关计算,使学生从中发现能拼成一个不
留空隙,又不重叠的平面图形的关键是几个多边形的内角和
相加要等于360°.
教学重点:通过用两种以上正多边形拼地板,提高学生观察、分析、概括、
抽象能力.
教学难点:寻找用哪几种正多边形能铺满地板的种类.
新知导入
情境引入
问题1
能用同一种正多边形铺满地板的都有谁?说一说,并从下图中找出
只有正三角形,正四边形,正六边形可以铺满地板.
新知讲解
合作学习
用相同的任意三角形、任意四边形能密铺吗?
思考
请各位同学以小组为单位随意剪出一些形状、大小都一样的四边形,拼拼看,能否铺满地面.
这是为什么呢?
小结:不规则四边形能用来铺地板的道理是:“任意四边形(指凸四边形)内角之和都等于360°。”因此,不管切下的四边形怎样歪七扭八,只要形状完全相同,4块相拼就能凑成360°,而且总能找到等长的边相接,使砖与砖之间不留缝隙.
结论:形状、大小相同的任意四边形能镶嵌成平面图形.
沙雅的妈妈让沙雅把一些形状,大小相同的三角形花布丢掉,不一会沙雅给妈妈拿来一块漂亮的桌布,沙雅是怎么做到的呢?
结论:形状、大小完全相同的任意三角形能镶嵌成平面图形.
规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.
用两种正多边形能密铺吗?
问题2
如图9.3.3,用正三角形和正六边形也能铺满地面.类似的情况还有吗
图9.3.3
1.正八边形和正方形组合.
135°+135°+90°=360°
正八边形的每一内角度数是135°,而正四边形的每一个内角是90°。两个135°与1个90°的和刚好是360°,
2.正十二边形和正三角形组合
150°+150°+60°=360°
正十二边形的每一内角度数是150°,而正三角形的每一个内角是60°。两个150°与1个60°的和刚好也是360°。
规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.
用三种正多边形能密铺吗?
问题3
90°
120°
150°
150°+120°+90°=360°
提炼概念
其他的图形是否也满足这一条件
当围绕一点拼在一起的几个多边形的内角和恰好组成一个周角时,就能铺满地面。
典例精讲
能扩展到整个平面,即铺满地面吗?
144°+108°+108°=360°
144°
108°
108°
例:正五边形、正十边形铺设地面
正五边形、正十边形铺设地面不能扩展到整个平面。
归纳概念
易错点:
有时几种正多边形的组合虽然能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面。
如正五边形和正十边形的组合。
或满足:
内角度数×m + 另一种内角度数×n+第三种内角度数×k =360°
的方程正整数解.
规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角(360°)时,就能铺满地面。
课堂练习
1.只用下列正多边形,能铺满地面的是( )
A.正五边形 B.正八边形 C.正六边形 D.正十边形
C
2.某中学新科技馆铺设地面,已有正三角形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则该学校不应该购买的地砖形状是( )
A.正方形 B.正六边形 C.正八边形 D.正十二边形
C
3、如图,是正在铺设的人行道上地板砖的部分,是由正六边形和四边形镶嵌而成的图形,则图中的四边形中的锐角∠BAD的度数是______度.
60
4、用正三角形和正六边形材料铺地面,在一个顶点周围有几个正三角形和几个正六边形?说明你的理由.
答:在一个顶点周围有4个正三角形和1个正六边形
或者在一个顶点周围有2个正三角形和2个正六边形
解:设在一个顶点周围有m个正三角形的角,n个正六边形的角。
由题意得 m×60°+ n×120°= 360°
即m+ 2n= 6 满足题意的正整数解为
m=4
n=1
m=2
n=2
或
课堂总结
用多种正多边形铺设地面
当围绕一点拼在一起的几个多边形的内角和恰好组成一个周角时,就能铺满地面。
有时几种正多边形的组合虽然能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面。
如正五边形和正十边形的组合。
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
