9.3.2 用多种正多边形铺设地面 学案(含答案)
文档属性
| 名称 | 9.3.2 用多种正多边形铺设地面 学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 21:58:09 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
9.3.2用多种正多边形铺设地面 导学案
课题 9.3.2用多种正多边形铺设地面 单元 第9单元 学科 数学 年级 七年级(下)
教材分析 在实验探究的学习活动中,使学生理解多种正多边形能够铺满地面的数学道理,掌握两种及两种以上的正多边形能够铺满地面的种类.探索用多种正多边形拼地板的过程和原理.
核心素养分析 (1)课堂上充分发挥学生的主体作用,通过小组合作学习,让学生在活动中实验、在实验中探索、在探索中领悟、在领悟中理解,从而能够很好地突出重点、突破难点.(2)通过对“用正多边形铺地板问题”的探究,让学生在参与中去体验、去感受、去领悟、去创造,激发学生的探究精神、培养创造能力.
学习目标 1.使学生理解多种正多边形能够铺满地面的数学道理,掌握两种及两种以上的正多边形能够铺满地面的种类.2.通过用两种以上正多边形拼地板,提高学生观察、分析、概括、抽象能力.
重点 通过用两种以上正多边形拼地板,提高学生观察、分析、概括、抽象能力.
难点 寻找用哪几种正多边形能铺满地板的种类.
教学过程
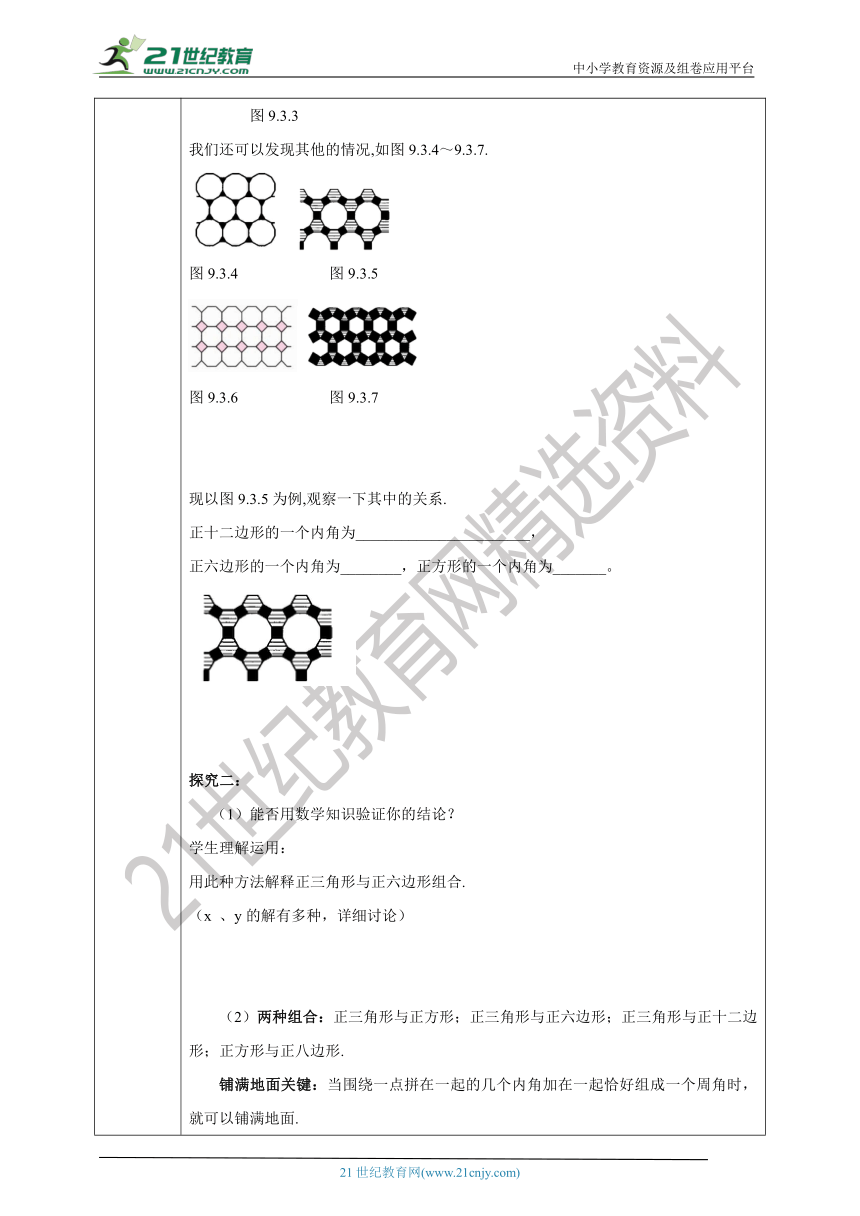
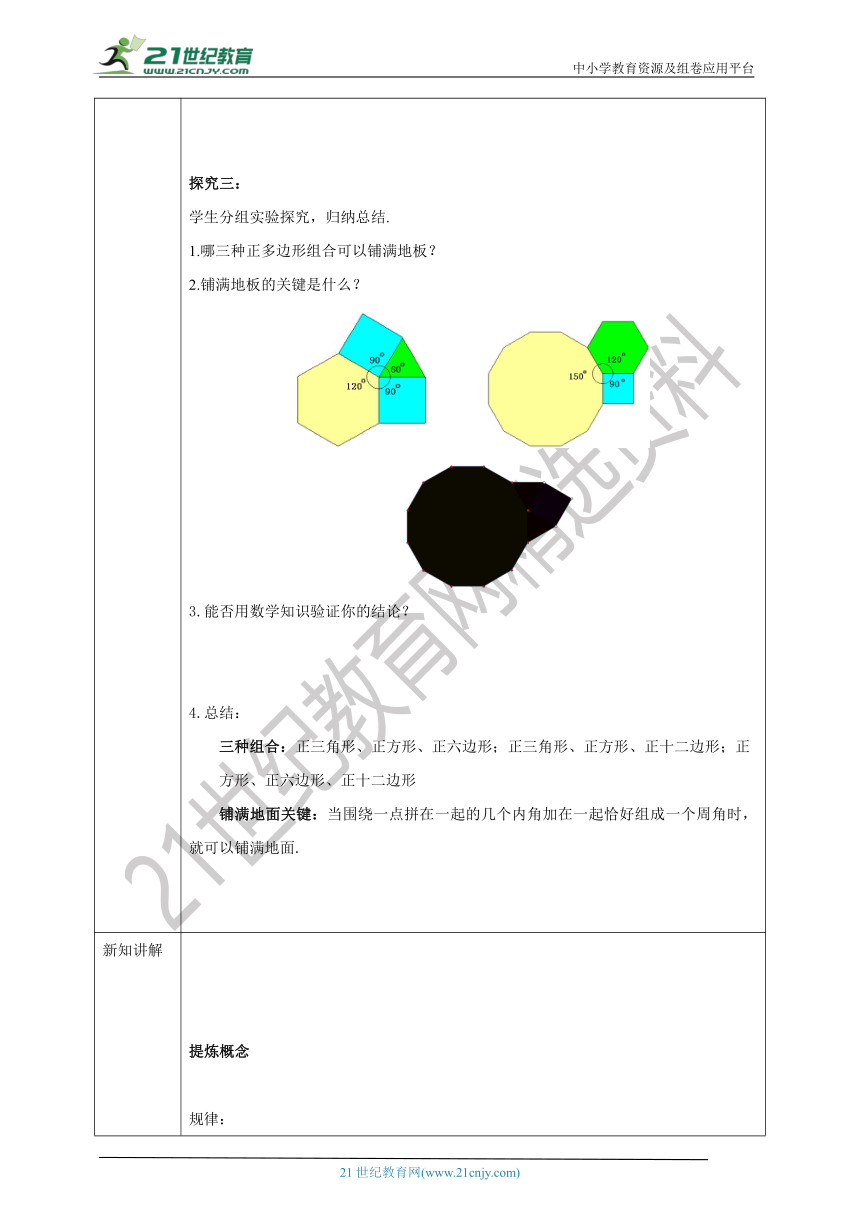
课前预学 引入思考说一说:①用不同正多边形是否也能铺满地面呢?如果可以,那么你能找出几种组合?你是如何找到的?问题:①用不同正多边形是否也能铺满地面呢?如果可以,那么你能找出几种组合?你是如何找到的?探究一:学生分组实验探究,归纳总结.(1)哪些正多边形两两组合可以铺满地板?(2)用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?如图9.3.3,用正三角形和正六边形也能铺满地面.类似的情况还有吗 图9.3.3我们还可以发现其他的情况,如图9.3.4~9.3.7.图9.3.4 图9.3.5图9.3.6 图9.3.7现以图9.3.5为例,观察一下其中的关系.正十二边形的一个内角为_______________________,正六边形的一个内角为________,正方形的一个内角为_______。探究二:(1)能否用数学知识验证你的结论? 学生理解运用:用此种方法解释正三角形与正六边形组合.(x 、y的解有多种,详细讨论)(2)两种组合:正三角形与正方形;正三角形与正六边形;正三角形与正十二边形;正方形与正八边形.铺满地面关键:当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.探究三:学生分组实验探究,归纳总结.1.哪三种正多边形组合可以铺满地板?2.铺满地板的关键是什么? 3.能否用数学知识验证你的结论? 4.总结:三种组合:正三角形、正方形、正六边形;正三角形、正方形、正十二边形;正方形、正六边形、正十二边形铺满地面关键:当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
新知讲解 提炼概念规律:当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.典例精讲 例:正五边形、正十边形铺设地面144°+108°+108°=360° 能扩展到整个平面,即铺满地面吗?正五边形、正十边形铺设地面________扩展到整个平面。思考:围绕一点拼在一起的两种正多边形的内角之和为360 ,是否就一定可以铺满地面了呢?
课堂练习 巩固训练1.只用下列正多边形,能铺满地面的是( ) A.正五边形 B.正八边形 C.正六边形 D.正十边形 2.某中学新科技馆铺设地面,已有正三角形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则该学校不应该购买的地砖形状是( )A.正方形 B.正六边形 C.正八边形 D.正十二边形 3、如图,是正在铺设的人行道上地板砖的部分,是由正六边形和四边形镶嵌而成的图形,则图中的四边形中的锐角∠BAD的度数是______度. 4、用正三角形和正六边形材料铺地面,在一个顶点周围有几个正三角形和几个正六边形?说明你的理由.答案引入思考 两种组合:正三角形与正方形;正三角形与正六边形;正三角形与正十二边形;正方形与正八边形.三种组合:正三角形、正方形、正六边形;正三角形、正方形、正十二边形;正方形、正六边形、正十二边形提炼概念规律:当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.典例精讲 例: 正五边形、正十边形铺设地面不能扩展到整个平面.巩固训练CC60
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
9.3.2用多种正多边形铺设地面 导学案
课题 9.3.2用多种正多边形铺设地面 单元 第9单元 学科 数学 年级 七年级(下)
教材分析 在实验探究的学习活动中,使学生理解多种正多边形能够铺满地面的数学道理,掌握两种及两种以上的正多边形能够铺满地面的种类.探索用多种正多边形拼地板的过程和原理.
核心素养分析 (1)课堂上充分发挥学生的主体作用,通过小组合作学习,让学生在活动中实验、在实验中探索、在探索中领悟、在领悟中理解,从而能够很好地突出重点、突破难点.(2)通过对“用正多边形铺地板问题”的探究,让学生在参与中去体验、去感受、去领悟、去创造,激发学生的探究精神、培养创造能力.
学习目标 1.使学生理解多种正多边形能够铺满地面的数学道理,掌握两种及两种以上的正多边形能够铺满地面的种类.2.通过用两种以上正多边形拼地板,提高学生观察、分析、概括、抽象能力.
重点 通过用两种以上正多边形拼地板,提高学生观察、分析、概括、抽象能力.
难点 寻找用哪几种正多边形能铺满地板的种类.
教学过程
课前预学 引入思考说一说:①用不同正多边形是否也能铺满地面呢?如果可以,那么你能找出几种组合?你是如何找到的?问题:①用不同正多边形是否也能铺满地面呢?如果可以,那么你能找出几种组合?你是如何找到的?探究一:学生分组实验探究,归纳总结.(1)哪些正多边形两两组合可以铺满地板?(2)用多种正多边形铺满地板,既不留空隙,又不重叠的关键是什么?如图9.3.3,用正三角形和正六边形也能铺满地面.类似的情况还有吗 图9.3.3我们还可以发现其他的情况,如图9.3.4~9.3.7.图9.3.4 图9.3.5图9.3.6 图9.3.7现以图9.3.5为例,观察一下其中的关系.正十二边形的一个内角为_______________________,正六边形的一个内角为________,正方形的一个内角为_______。探究二:(1)能否用数学知识验证你的结论? 学生理解运用:用此种方法解释正三角形与正六边形组合.(x 、y的解有多种,详细讨论)(2)两种组合:正三角形与正方形;正三角形与正六边形;正三角形与正十二边形;正方形与正八边形.铺满地面关键:当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.探究三:学生分组实验探究,归纳总结.1.哪三种正多边形组合可以铺满地板?2.铺满地板的关键是什么? 3.能否用数学知识验证你的结论? 4.总结:三种组合:正三角形、正方形、正六边形;正三角形、正方形、正十二边形;正方形、正六边形、正十二边形铺满地面关键:当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
新知讲解 提炼概念规律:当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.典例精讲 例:正五边形、正十边形铺设地面144°+108°+108°=360° 能扩展到整个平面,即铺满地面吗?正五边形、正十边形铺设地面________扩展到整个平面。思考:围绕一点拼在一起的两种正多边形的内角之和为360 ,是否就一定可以铺满地面了呢?
课堂练习 巩固训练1.只用下列正多边形,能铺满地面的是( ) A.正五边形 B.正八边形 C.正六边形 D.正十边形 2.某中学新科技馆铺设地面,已有正三角形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则该学校不应该购买的地砖形状是( )A.正方形 B.正六边形 C.正八边形 D.正十二边形 3、如图,是正在铺设的人行道上地板砖的部分,是由正六边形和四边形镶嵌而成的图形,则图中的四边形中的锐角∠BAD的度数是______度. 4、用正三角形和正六边形材料铺地面,在一个顶点周围有几个正三角形和几个正六边形?说明你的理由.答案引入思考 两种组合:正三角形与正方形;正三角形与正六边形;正三角形与正十二边形;正方形与正八边形.三种组合:正三角形、正方形、正六边形;正三角形、正方形、正十二边形;正方形、正六边形、正十二边形提炼概念规律:当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面.典例精讲 例: 正五边形、正十边形铺设地面不能扩展到整个平面.巩固训练CC60
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
