人教版数学七年级下册6.3实数 说课课件(共30张PPT)
文档属性
| 名称 | 人教版数学七年级下册6.3实数 说课课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
人教版
七年级《实数》
一、教学分析
二、教学策略
四、课例分析
三、学情分析
实数
五、教学反思
一、教学分析
(一).教材所处的地位和作用
从《数学课程标准》看,关于数的内容,初中学段主要学习有理数和实数,它们是“数与代数”领域的重要内容。本章是在学生学习了“有理数”的基础上进行的,可以看成其后的代数内容的起始章,也是学习“二次根式”的基础,起着呈上启下的作用。
教学分析
本章首先介绍平方根与立方根的概念,并通过开平方、开立方运算认识一些不同于有理数的数,在此基础上引入无理数,把数的范围扩充到实数;类比有理数,引入实数在数轴上的表示和实数的运算;并用这些知识解决一些实际问题.通过本章的学习,学生对数的认识就由有理数范围扩大到实数范围.本章之前的数学内容都是在有理数范围内讨论的,学习本章之后,将在实数范围内研究问题.虽然本章的内容不多,篇幅不大,但在中学数学中占有重要地位,本章内容不仅是后续学习二次根式、一元二次方程以及锐角三角函数等知识的基础,也是学习高中数学中函数、不等式以及解析几何等知识的基础.
教学分析
(二)新课标基本要求
1.了解算术平方根、平方根、立方根的概念,会用根号表示数的算数平方根、平方根、立方根。
2.了解乘方与开方互为逆运算,会用平方运算求百以内整数的平方根及立方根,会用计算器求平方根及立方根。
3.了解无理数和实数的概念,知道实数与数轴上的点一一对应,能求实数的相反数与绝对值。
教学分析
4.能用有理数估计一个无理数的大致范围。
5.了解近似数,在解决实际问题中,能用计算器进行近似计算,并会按问题的要求对结果取近似值。
6.了解二次根式、最简二次根式的概念,了解二次根式加减乘除运算法则,会用它们进行相关的简单四则运算。
教材分析
教学重点分析
1、平方根和算术平方根的概念。
2、立方根的概念与性质及求法。
3、无理数和实数的概念。
教材分析
教学难点
1、平方根与算术平方根的区别与联系。
2、立方根的唯一性及负数立方根的意义。
3、无理数和实数的理解。
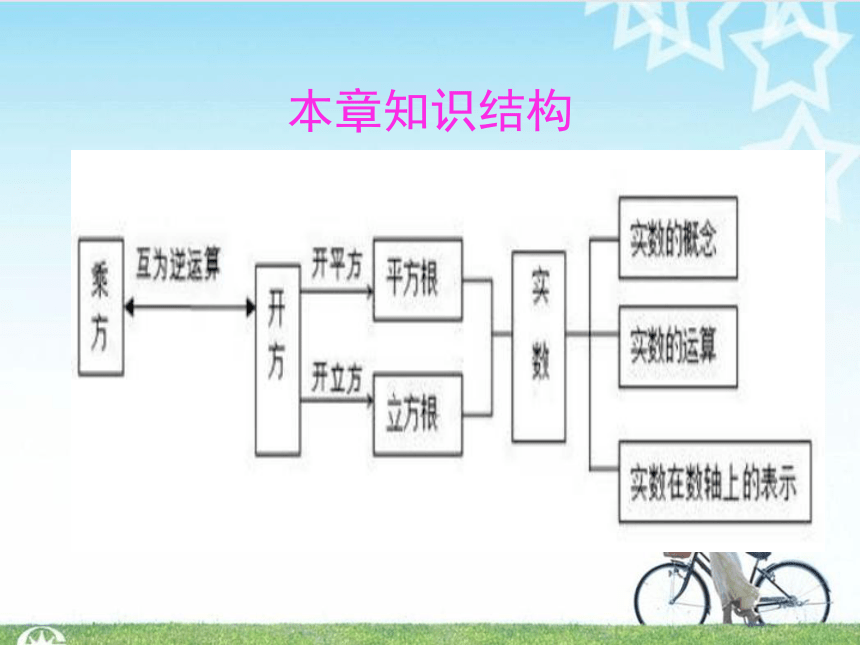
本章知识结构
立方根
实数
实数
培养学生自主探索的精神
平方根
经历算术平方根和平方根概念的形成,并了解其定义和性质
会求某些正数的算数平方根和平方根,并会用符号表示
会用计算器求一个非负数的算数平方根,会估算一个正数的算术平方根的近似值
了解立方根的定义,并会表示一个数的立方根
了解开立方和立方互为逆运算,会求一个数的立方根
体会一个数的立方根的唯一性,分清立方根与平方根的区别
会用计算器求一个数的立方根
了解无理数和实数的定义及其分类
能用一个有理数估计无理数的范围
课时安排
6.1平方根 3课时
6.2立方根 2课时
6.3实数 2课时
数学活动与小结 1课时
二、教学策略
(一)加强与实际的联系
本章内容与实际的联系是非常密切的。例如,无理数是从现实世界中抽象出来的一种数,开平方运算和开立方运算也是实际中经常用到的两种运算,用有理数估计无理数的大小在现实生活中经常遇到等等。因此,在进行本章教学时应注意联系实际,对于一些重要的概念和运算紧密结合实际生活展开,例如算术平方根是从已知正方形的面积求它边长、立方根是从已知立方体的体积求它边长等典型的实际问题引出,再如用有理数估计无理数的大小也是紧密结合实际进行的,将本章内容与实际紧密联系起来,可以使学生在解决实际问题的过程中,认识实数的有关概念和运算。
教学策略
(二)加强知识间的纵向联系
学生在七年级上册已经系统地学过有理数,对有理数的概念和运算等有了较深刻的认识,本章是在有理数的基础上学习实数的初步知识,是有理数相关内容的延续和推广,因此,在教学中要注意加强知识间的相互联系,使学生更好地体会数的扩充过程中表现出来的概念、运算等的一致性和发展变化。例如,对于绝对值和相反数的概念,实数的运算法则和运算性质等都是在有理数的基础上展开的。另外,本章前两节“平方根”“立方根”在内容上基本是平行的,因此,在学习“立方根”这节时,可以充分利用类比的方法,引入立方根的概念,以及开立方运算,这样有助于加强知识间的相互联系,通过类比已学的知识学习新知识,使学生的学习形成正迁移。
教学策略
(三)留给学生探索交流的空间
根据本章内容的特点,对于一些重要的概念和结论,本章采用让学生通过观察、思考、讨论等探究活动归纳得出结论。在讨论数的立方根的特征时,教材首先设置“探究”栏目,在栏目中以填空的方式让学生计算一些具体的正数、负数和0的立方根,寻找它们各自的特点,通过学生讨论交流等活动,归纳得出“正数的立方根是正数,0的立方根是0,负数的立方根是负数”的结论,这样就让学生通过探究活动经历了一个由特殊到一般的认识过程,在探究活动的过程中发展思维能力,有效改变学生的学习方式。
学情分析
(一)知识层面
本章属于初中“数与代数”领域的第二部分内容,第一部分内容“有理数”学生在上期第一章中已经学习过了,但与本章学习时间相隔较长,很多学生已经对重要内容有所遗忘,所以在讲授时应该对个别知识点进行系统地回顾和练习。
学情分析
(二)学生特点分析
七年级下期学生思想浮动较大,差距也渐渐拉开,许多基础不好的学生会丧失学好数学的信心,本章知识比较简单,教师在讲授时应多关注后进生的学习状况,增加其自信心。
6.1 平方根
(第1课时)
学习目标:
(1)了解算术平方根的概念.
(2)会求一些数的算术平方根,并用算术平方根符号表示.
学习重难点:
算术平方根的概念和求法.
请你说一说解决问题的思路.
1.情境导入
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
例如,由于 ,5是25的算术平方根,
即 .
一般地,如果一个正数的平方等于 , 即 ,那么这个正数 叫做 的算术
平方根. 的算术平方根记为 ,读作
“根号 ”, 叫做被开方数.
2.归纳概念(自学,3分钟)
例1 求下列各数的算术平方根:
(1) ;(2) ;(3) .
解:(1)因为 ,
所以100的算术平方根是10 .
即 .
3.例题解析
针对练习
1、填空:
(1)因为_____2=64,所以64的算术平方根是______,即 =______;
(2)因为_____2=0.25,所以0.25的算术平方根是______,即 =______;
求下列各式的值:
(1) ;(2) ;(3) ;(4) .
解:(1) ; (2) ;
(3) ; (4) .
2.练习(四号展示,时间3分钟)
4.提出问题(小组讨论,交流3分钟)
被开方数的大小与对应的算术平方根的大小之间有什么关系呢?
-4有算术平方根吗?什么数才有算术平方根?
例2 下列各式是否有意义,为什么?
(1) ;(2) ;(3) ;(4) .
解:
(1)无意义;
(4)有意义.
(3)有意义;
(2)有意义;
5.例题解析
(1)什么是算术平方根?
如何求一个正数的算术平方根?
(2) 什么数才有算术平方根?
6.畅谈收获
教科书41页 练习 第1、2题
8.布置作业
教学反思
总之,在教学过程中,我始终注意发挥学生的主体作用,让学生通过自主、探究、合作学习来主动发现结论,实现师生互动,我认识到教师不仅要教给学生知识,更要培养学生良好的数学素养和学习习惯,让学生学会学习,这样才能使自己成为一名受学生欢迎的好教师!
人教版
七年级《实数》
一、教学分析
二、教学策略
四、课例分析
三、学情分析
实数
五、教学反思
一、教学分析
(一).教材所处的地位和作用
从《数学课程标准》看,关于数的内容,初中学段主要学习有理数和实数,它们是“数与代数”领域的重要内容。本章是在学生学习了“有理数”的基础上进行的,可以看成其后的代数内容的起始章,也是学习“二次根式”的基础,起着呈上启下的作用。
教学分析
本章首先介绍平方根与立方根的概念,并通过开平方、开立方运算认识一些不同于有理数的数,在此基础上引入无理数,把数的范围扩充到实数;类比有理数,引入实数在数轴上的表示和实数的运算;并用这些知识解决一些实际问题.通过本章的学习,学生对数的认识就由有理数范围扩大到实数范围.本章之前的数学内容都是在有理数范围内讨论的,学习本章之后,将在实数范围内研究问题.虽然本章的内容不多,篇幅不大,但在中学数学中占有重要地位,本章内容不仅是后续学习二次根式、一元二次方程以及锐角三角函数等知识的基础,也是学习高中数学中函数、不等式以及解析几何等知识的基础.
教学分析
(二)新课标基本要求
1.了解算术平方根、平方根、立方根的概念,会用根号表示数的算数平方根、平方根、立方根。
2.了解乘方与开方互为逆运算,会用平方运算求百以内整数的平方根及立方根,会用计算器求平方根及立方根。
3.了解无理数和实数的概念,知道实数与数轴上的点一一对应,能求实数的相反数与绝对值。
教学分析
4.能用有理数估计一个无理数的大致范围。
5.了解近似数,在解决实际问题中,能用计算器进行近似计算,并会按问题的要求对结果取近似值。
6.了解二次根式、最简二次根式的概念,了解二次根式加减乘除运算法则,会用它们进行相关的简单四则运算。
教材分析
教学重点分析
1、平方根和算术平方根的概念。
2、立方根的概念与性质及求法。
3、无理数和实数的概念。
教材分析
教学难点
1、平方根与算术平方根的区别与联系。
2、立方根的唯一性及负数立方根的意义。
3、无理数和实数的理解。
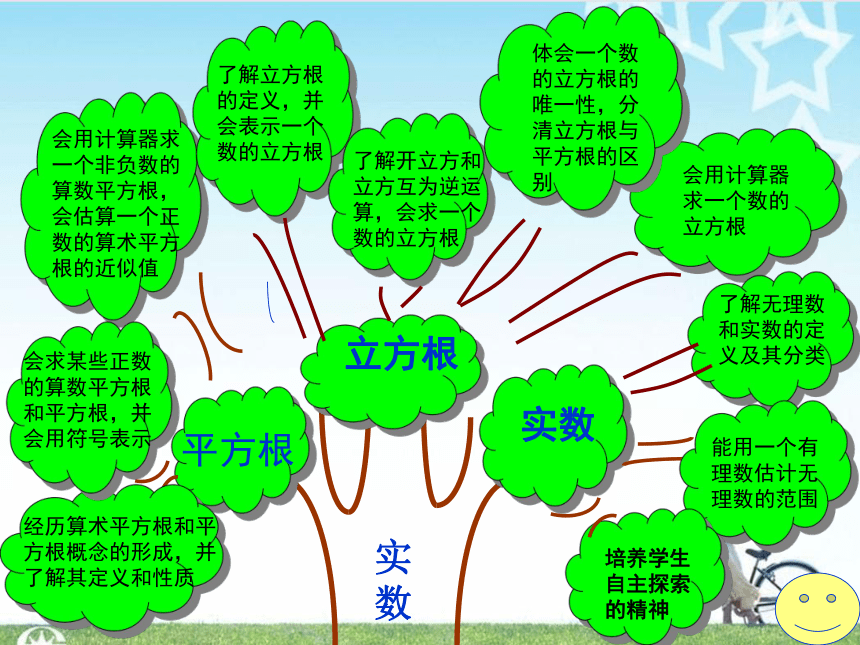
本章知识结构
立方根
实数
实数
培养学生自主探索的精神
平方根
经历算术平方根和平方根概念的形成,并了解其定义和性质
会求某些正数的算数平方根和平方根,并会用符号表示
会用计算器求一个非负数的算数平方根,会估算一个正数的算术平方根的近似值
了解立方根的定义,并会表示一个数的立方根
了解开立方和立方互为逆运算,会求一个数的立方根
体会一个数的立方根的唯一性,分清立方根与平方根的区别
会用计算器求一个数的立方根
了解无理数和实数的定义及其分类
能用一个有理数估计无理数的范围
课时安排
6.1平方根 3课时
6.2立方根 2课时
6.3实数 2课时
数学活动与小结 1课时
二、教学策略
(一)加强与实际的联系
本章内容与实际的联系是非常密切的。例如,无理数是从现实世界中抽象出来的一种数,开平方运算和开立方运算也是实际中经常用到的两种运算,用有理数估计无理数的大小在现实生活中经常遇到等等。因此,在进行本章教学时应注意联系实际,对于一些重要的概念和运算紧密结合实际生活展开,例如算术平方根是从已知正方形的面积求它边长、立方根是从已知立方体的体积求它边长等典型的实际问题引出,再如用有理数估计无理数的大小也是紧密结合实际进行的,将本章内容与实际紧密联系起来,可以使学生在解决实际问题的过程中,认识实数的有关概念和运算。
教学策略
(二)加强知识间的纵向联系
学生在七年级上册已经系统地学过有理数,对有理数的概念和运算等有了较深刻的认识,本章是在有理数的基础上学习实数的初步知识,是有理数相关内容的延续和推广,因此,在教学中要注意加强知识间的相互联系,使学生更好地体会数的扩充过程中表现出来的概念、运算等的一致性和发展变化。例如,对于绝对值和相反数的概念,实数的运算法则和运算性质等都是在有理数的基础上展开的。另外,本章前两节“平方根”“立方根”在内容上基本是平行的,因此,在学习“立方根”这节时,可以充分利用类比的方法,引入立方根的概念,以及开立方运算,这样有助于加强知识间的相互联系,通过类比已学的知识学习新知识,使学生的学习形成正迁移。
教学策略
(三)留给学生探索交流的空间
根据本章内容的特点,对于一些重要的概念和结论,本章采用让学生通过观察、思考、讨论等探究活动归纳得出结论。在讨论数的立方根的特征时,教材首先设置“探究”栏目,在栏目中以填空的方式让学生计算一些具体的正数、负数和0的立方根,寻找它们各自的特点,通过学生讨论交流等活动,归纳得出“正数的立方根是正数,0的立方根是0,负数的立方根是负数”的结论,这样就让学生通过探究活动经历了一个由特殊到一般的认识过程,在探究活动的过程中发展思维能力,有效改变学生的学习方式。
学情分析
(一)知识层面
本章属于初中“数与代数”领域的第二部分内容,第一部分内容“有理数”学生在上期第一章中已经学习过了,但与本章学习时间相隔较长,很多学生已经对重要内容有所遗忘,所以在讲授时应该对个别知识点进行系统地回顾和练习。
学情分析
(二)学生特点分析
七年级下期学生思想浮动较大,差距也渐渐拉开,许多基础不好的学生会丧失学好数学的信心,本章知识比较简单,教师在讲授时应多关注后进生的学习状况,增加其自信心。
6.1 平方根
(第1课时)
学习目标:
(1)了解算术平方根的概念.
(2)会求一些数的算术平方根,并用算术平方根符号表示.
学习重难点:
算术平方根的概念和求法.
请你说一说解决问题的思路.
1.情境导入
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
例如,由于 ,5是25的算术平方根,
即 .
一般地,如果一个正数的平方等于 , 即 ,那么这个正数 叫做 的算术
平方根. 的算术平方根记为 ,读作
“根号 ”, 叫做被开方数.
2.归纳概念(自学,3分钟)
例1 求下列各数的算术平方根:
(1) ;(2) ;(3) .
解:(1)因为 ,
所以100的算术平方根是10 .
即 .
3.例题解析
针对练习
1、填空:
(1)因为_____2=64,所以64的算术平方根是______,即 =______;
(2)因为_____2=0.25,所以0.25的算术平方根是______,即 =______;
求下列各式的值:
(1) ;(2) ;(3) ;(4) .
解:(1) ; (2) ;
(3) ; (4) .
2.练习(四号展示,时间3分钟)
4.提出问题(小组讨论,交流3分钟)
被开方数的大小与对应的算术平方根的大小之间有什么关系呢?
-4有算术平方根吗?什么数才有算术平方根?
例2 下列各式是否有意义,为什么?
(1) ;(2) ;(3) ;(4) .
解:
(1)无意义;
(4)有意义.
(3)有意义;
(2)有意义;
5.例题解析
(1)什么是算术平方根?
如何求一个正数的算术平方根?
(2) 什么数才有算术平方根?
6.畅谈收获
教科书41页 练习 第1、2题
8.布置作业
教学反思
总之,在教学过程中,我始终注意发挥学生的主体作用,让学生通过自主、探究、合作学习来主动发现结论,实现师生互动,我认识到教师不仅要教给学生知识,更要培养学生良好的数学素养和学习习惯,让学生学会学习,这样才能使自己成为一名受学生欢迎的好教师!
