直线与圆的位置关系

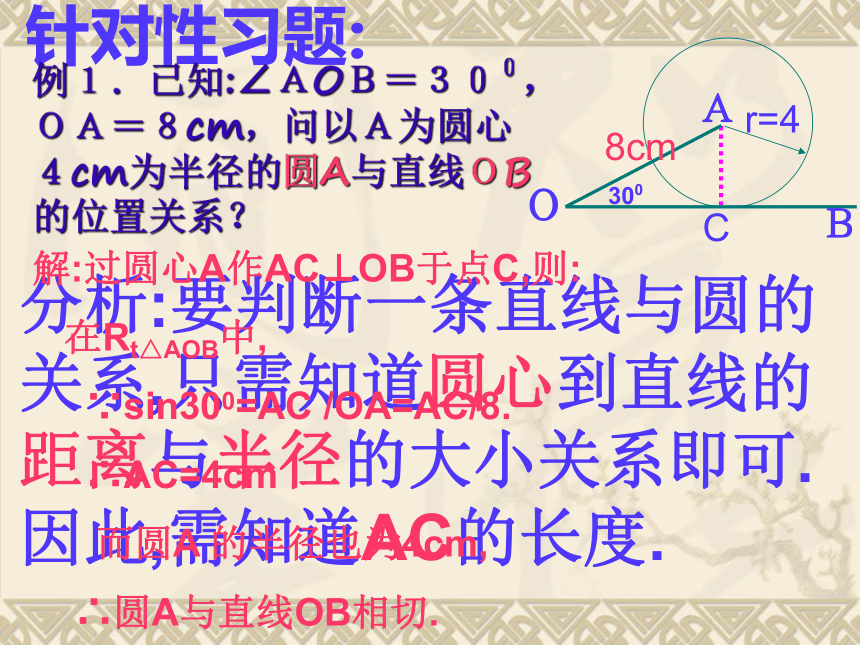
课件12张PPT。 二００ 六 年 十 一 月 五 日 制 作 与圆有关的位置关系(一)__直线与圆的位置关系数学是思维的体操!学习目的：　　●．探索并了解直线与圆的位置关系.●.能够利用直线与圆的位置关系解决问题.数学是思维的体操!●.重点掌握直线与圆相切.AAB1.相离:如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离.(d>R)2.相切:如果一条直线与一个圆有且只有一个公共点,那么就说这条直线与这个圆相切.这时,这条直线叫做圆的切线,这个公共点叫做切点.(d=R)3.相交:如果一条直线与一个圆有两个交点,那么就说这条直线与这个圆相交.这时,这条直线叫圆的割线.(d 在Rt△AOB中,
∵sin300=AC /OA=AC/8.
∴AC=4cm
而圆A 的半径也为4cm,
∴圆A与直线OB相切.
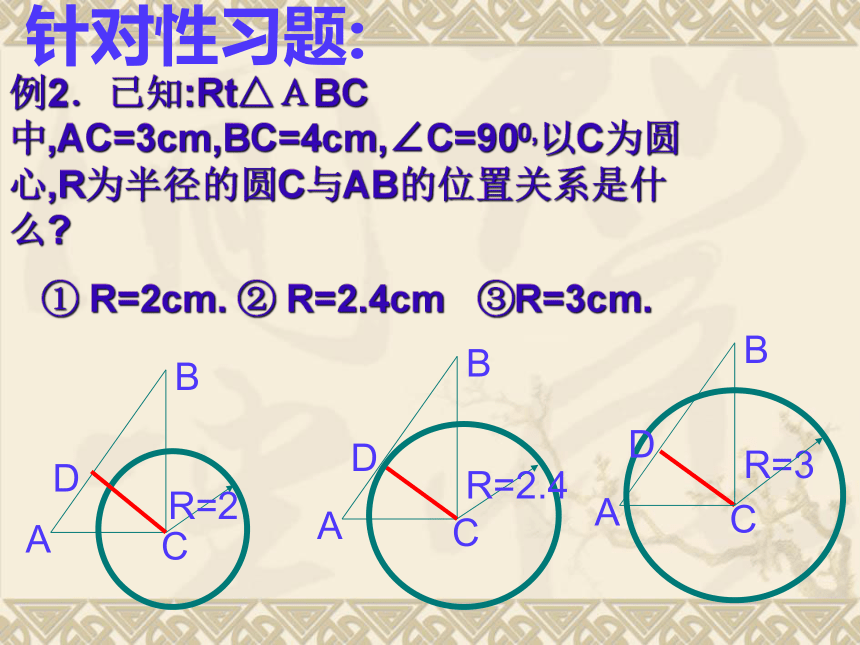
针对性习题:例2．已知:Rt△ＡBC 中,AC=3cm,BC=4cm,∠C=900,以C为圆心,R为半径的圆C与AB的位置关系是什么?
① R=2cm. ② R=2.4cm ③R=3cm. DDR=2.4DR=3解:过C作CD⊥AB于点D , 在Rt△ABC中.
由勾股定理得: AB= 5(cm),
根据三角形的面积公式有
CD·AB=AC·BC ∴CD=AC·BC/AB
=3×4/5 = 2.4(cm)
即:d=2.4cm
⑴ 当R=2cm时,有d>R, 因此⊙C与AB相离. ⑵当R=2.4cm时,有d=R, 因此⊙C与AB相切.⑶ 当R=3cm时,有d 求证:直线AB是⊙O的切线.COAB
∵OA=OB,CA=CB,
∴OC是等腰三角形OAB底边AB上的 中线.
∴AB⊥OC
直线AB经过半径OC的外端C,并且垂直于半径OC. 所以AB是⊙O的切线.证明:连结OC.
分析:要证AB是⊙O 的切线,由切线的判定定理则需证AB过⊙O的一条半径的外端点,且与该半径垂直.所以可以连结OC构造出一条半径(OC),由于AB经过点C(已知条件),因此只需再想办法证明AB⊥OC即可!当堂作业:
1.如图:AB是⊙O的直径,∠ABT=450,AT=AB.
求证:AT是⊙O的切线.2.AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=300.
求证 :DC是⊙O的切线. 4.如图,AB是⊙O的直径,⊙O过BC的中点D,DE⊥AC.
求证:DE是⊙O的切线.5.已知,如图,△ABC内接于⊙O,AB是直径,∠CAE=∠B.求证:AE与⊙O相切于点A.人人学有价值的数学! 谢谢大家 　　　　　　　　　　再见！人人学有价值的数学；人人都能获得必须的数学；不同的人在数学上得到不同的发展！ 2 0 0 6 年 11 月 5 日 制 作