直线与圆的位置关系

课件31张PPT。新课标华东师大版实验教材九年级上册《直线与圆的位置关系》重庆江北区华渝实验学校 赵剑萍
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
教材所处的地位和作用学生的现实情况教学目标教学重难点
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
１、教材所处的地位和作用本章：探索特殊的曲线形——圆。学好本章内容，能提高解题的综合分析能力。本部分：研究点、直线、圆的相互位置关系及数量关系，有利于学生合情推理水平的提高。本节：对知识的衔接有承上启下的作用。
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
2、学生的现实情况 我校是一所普通中学，存在部分求知欲强烈、思维活跃的学生，但总体上学生接受和运用新知识较慢，学习能力有待提高。
3、教学目标知识与技能过程与方法情感态度、价值观①了解直线与圆有三种位置关系，能概括其定义
②掌握直线与圆位置关系的两种判断方法
③能较灵活的运用直线与圆位置关系的数量关系①经历观察、比较等数学活动
②体会“类比”、“数形结合”等数学思想
的运用①体验数学活动中的探索与创造，获得成功的喜悦；
②在独立思考的基础上，积极参与对数学问题的讨论与交流，从中获益。一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
4、教学重、难点重点：探究直线与圆位置关系的数量关系 难点：用数形结合的思想研究直线与圆的
位置关系 一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
教法分析学法分析启导式教学法
讲练结合法一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
动脑、动手、动口
观察、实验、交流
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（一）创设情景、孕育新知 使至塞上(唐 王维）一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（一）创设情景、孕育新知 使至塞上(唐 王维）
长河落日圆一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
看成怎样的几何图形呢？大漠孤烟直
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
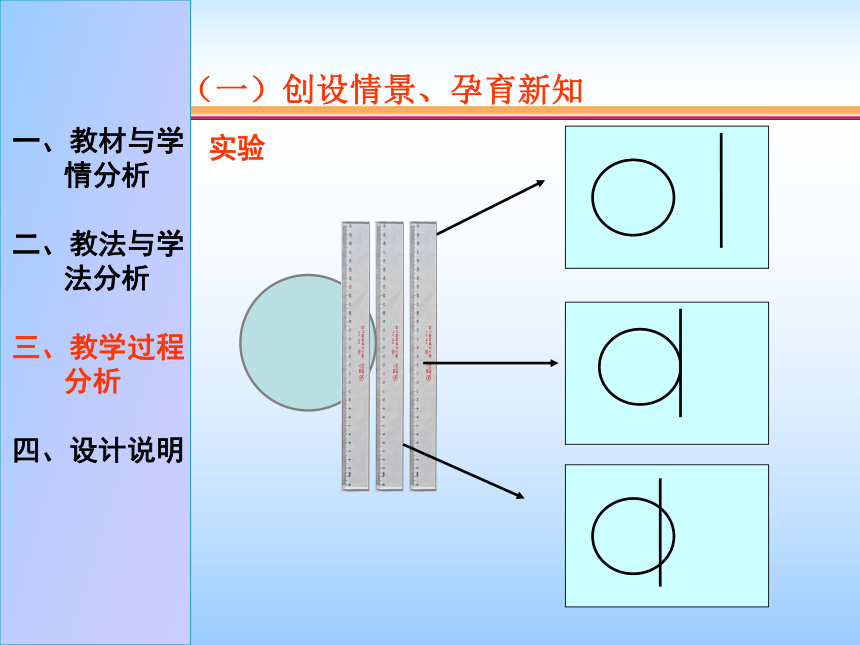
（一）创设情景、孕育新知 实验
直线与圆的位置关系一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（二）启发诱导、探索结论1、提出问题
（1）概括直线与圆的有哪几种位置关系，你是怎样区分这几种位置关系的？
（2）如何用语言描述这几种位置关系？
（3）回顾点与圆的位置关系，你能不能探索出圆心到直线的距离与圆的半径之间有怎样的数量关系？一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
2、学习新知（问题1） “形”（二）启发诱导、探索结论一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
相离没有公共点相切只有一个公共点相交两个公共点直线与圆的公共点个数判
断直线与圆的位置关系切线割线切点
（二）启发诱导、探索结论
（1）概括直线与圆的有哪几种位置关系，你是怎样区分这几种位置关系的？
（2）如何用语言描述这几种位置关系？
（3）回顾点与圆的位置关系，你能不能探索出圆心到直线的距离与圆的半径之间有怎样的数量关系？一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
1、提出问题
（二）启发诱导、探索结论一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
OABCd1d2d3r点A在圆外 d1>r 点B在圆上 d2=r问题2、这种方法能否用来确定直线与圆是哪种位置关系？ 问题1：怎样确定一个点与圆到底是哪种位置关系？ 点C在圆内 d3一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（二）启发诱导、探索结论观
察
1rd是什么引起直线与圆的位置关系发生改变的？没有公共点只有一个公共点有两个公共点2、学习新知（问题3） “数”→“形”
（二）启发诱导、探索结论一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
结
论
1dr圆心到直线的距离与圆半径的数量
关系可以判断直线与圆位置关系没有公共点只有一个公共点有两个公共点d>r→相离d=r→
相切d（二）启发诱导、探索结论一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
想
一
想相离时
d>r?
相切时d=r?
d相交时d2、学习新知（问题3） “形”→“数”
（二）启发诱导、探索结论一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
结
论
2r相离时
d>r
相切时d=r
相交时dd2、学习新知（问题3） “形”→“数”理论依据：垂线段最短
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
结论3：
直线与圆相离 d?r
直线与圆相切 d=r
直线与圆相交 d?r

（位置关系）互逆（数量关系）
（二）启发诱导、探索结论
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（三）讲练结合、巩固新知例2、已知Rt△ABC的斜边AB=6cm，直角边AC=3cm。圆心为A，半径分别为2cm、4cm的两个圆与直线BC有怎样的位置关系？半径r多长时，BC与⊙A相切？变式1、在上题中，圆心为C，半径分别为
2cm、4cm的两个圆与直线AB有怎样的位
置关系？半径r多长时，直线AB与⊙C相
切？
例1、已知圆的直径为10cm，圆心到直线l的距离是：（1）3cm ；（2）5cm ；（3）7cm。直线和圆有几个公共点？为什么？变式2、在上题中，若将直线AB改为边AB，
⊙C与边AB相交，则圆半径r应取怎样
的值？变式训练，挑战自我
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（三）讲练结合、巩固新知(备用练习）
一、选择题：
1、已知△ABC中，∠C=90°，CD⊥AB于D，AD=2，BD=1，以C为圆心，1.4为半径的圆与直线AB的关系是（ ）
A 相切 B 相交 C 相离 D 相切或相离
2、等腰△ABC的腰AB=AC=4，若以A为圆心，2为半径的圆与BC相切，则∠BAC的度数为（ ）
A 30° B 60° C 90° D 120°
二、解答题
1、已知∠AOC= 60°，点B在OA上，且OB=2 ，若以B为圆心，R为半径的圆与直线OC相离，则R的取值范围是多少？
2、Rt△ABC中，∠A= 30°，点O在AB上，
OD⊥AC于D。设AO=x，☉O的半径为1，问：
当x在什么范围内取值时，AC与☉O相离、
相切、相交？

一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（四）知识拓展、深化提高《数学课程标准》指出：学生的数学学习内容应该是现实的、有意义的、富有挑战性的。数学知识来源于生活，并拓展应用于生活。学生间的差异却是客观存在的。
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（四）知识拓展、深化提高 在某张航海图上，标明了三个观测点的坐标，如图， O（0，0），B（6，0），C（6，8），由三个观测点确定的圆形区域是海洋生物保护区。 1、求圆形区域的面积；
2、某时刻海面上出现一渔船A，在观察点O测得A位于北偏东45°，同时在观测点B测得A位于北偏东30°，那么当渔船A向正西方向航行时，是否会进入海洋生物保护区？A
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（五） 小结新知、画龙点睛我的数学日记
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
1、内容小结：
直线与圆相离 无公共点 d>r
直线与圆相切 只有一个公共点 d=r
直线与圆相交 有两个公共点 d数形结合、转化与化归、类比、数学建模（五） 小结新知、画龙点睛
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
（六）布置作业、复习巩固3、阅读材料：古诗云：“欲穷千里目，更上一层楼”。但是，若我们“更上一层楼”时，且没有任何障碍物遮挡视线，是否真的能“穷千里目”呢？把地球的剖面看作圆形，半径是R，人站在地球表面上空的P处，切点T即为人的视线在地球表面的终点（假定没有任何障碍物遮挡视线）…… 所以，在地球表面上，“欲穷千里目”靠“更上一层楼”来实现是根本办不到的。1、阅读教材55、56页
2、P56练习1.2.3。
一、教材与学情分析
二、教法与学 法分析
三、教学过程分析
四、设计说明
学生应学会学习 教师应重视方法 《数学课程标准》明确指出：学生是学习的主人。有效的数学学习活动不能单纯的依赖于模仿与记忆。“教是为了不教”。“学会学习，为终身学习作准备”。 教师尽量提供给学生“多观察、勤思考、多交流、勤钻研”的空间，有意识地培养学生学数学的主动性。使学生真正做到“学会学习”。 谢谢大家
请多指教美丽的重庆欢迎您