人教版八年级上册 18.2.2 菱形 教案(表格式 无答案)
文档属性
| 名称 | 人教版八年级上册 18.2.2 菱形 教案(表格式 无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 09:37:56 | ||
图片预览

文档简介
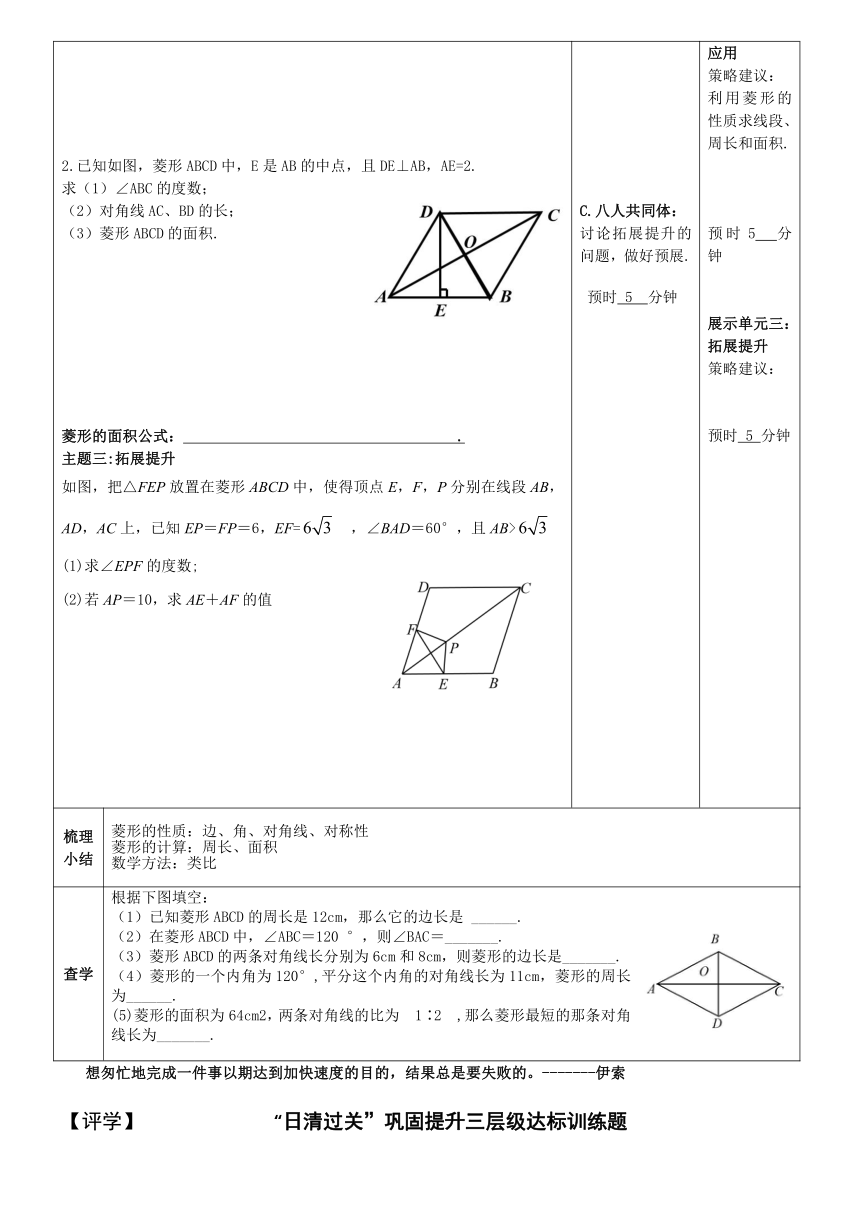
课题: 18.2.2菱形(1) 课型:预展课
学习目标:1.了解菱形的概念及其与平行四边形的关系.
2.探索并证明菱形的性质定理.
3.应用菱形的性质定理解决相关计算或证明问题.
学习重点: 探索并证明菱形的性质定理.
学习难点:应用菱形的性质定理解决相关计算或证明问题.
【展示课导学】
独学 合学 展学
主题一:菱形的定义与性质 问题1 如果从边的角度,将平行四边形特殊化,让它有一组邻边相等,这个特殊的四边形叫什么呢 定义: 叫做菱形. 思考:菱形与平行四边形的区别与联系? 问题2 请剪出一个菱形并观察,菱形是轴对称图形吗 若是,指出它的对称轴. 问题3 根据剪纸的过程,猜想菱形的四边在数量上有什么关系 菱形的两对角线有什么关系 请证明你的猜想: 归纳:菱形的性质并用几何语言表示 (1)菱形的四条边都 . (2)菱形的两条对角线 . 几何语言: 主题二:菱形的性质应用 1.如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长. 2.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2. 求(1)∠ABC的度数; (2)对角线AC、BD的长; (3)菱形ABCD的面积. 菱形的面积公式: . 主题三:拓展提升 如图,把△FEP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF= ,∠BAD=60°,且AB> (1)求∠EPF的度数;
(2)若AP=10,求AE+AF的值
A.两人小对子: 讨论菱形的定义,性质及其证明,明确菱形与平行四边形的区别与联系. 预时 5 分钟 B.四人互助组: 讨论菱形的性质应用,解决周长、面积等几何问题,明确菱形的面积计算公式. 预时 5 分钟 C.八人共同体: 讨论拓展提升的问题,做好预展. 预时 5 分钟 展示单元一:菱形的定义与性质 策略建议: 菱形的定义及与平行四边形的关系; 菱形的性质探索证明. 预时 5 分钟 展示单元二:菱形性质的应用 策略建议: 利用菱形的性质求线段、周长和面积. 预时5 分钟 展示单元三:拓展提升 策略建议: 预时 5 分钟
梳理小结 菱形的性质:边、角、对角线、对称性 菱形的计算:周长、面积 数学方法:类比
查学 根据下图填空: (1)已知菱形ABCD的周长是12cm,那么它的边长是 ______. (2)在菱形ABCD中,∠ABC=120 °,则∠BAC=_______. (3)菱形ABCD的两条对角线长分别为6cm和8cm,则菱形的边长是_______. (4)菱形的一个内角为120°,平分这个内角的对角线长为11cm,菱形的周长为______. (5)菱形的面积为64cm2,两条对角线的比为 1∶2 ,那么菱形最短的那条对角线长为_______.
想匆忙地完成一件事以期达到加快速度的目的,结果总是要失败的。-------伊索
【评学】 “日清过关”巩固提升三层级达标训练题
课题: 18.2.2菱形(1) 班级_______________ 姓名______________
一 基础题
1.菱形具有而矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线互相垂直 C.对角线相等 D.四个角都相等
2.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是 ( )
A.M(5,0),N(8,4) B.M(4,0),N(8,4)
C.M(5,0),N(7,4) D.M(4,0),N(7,4)
3.已知菱形ABCD中,AE⊥BC于E,若S菱形ABCD=24,且AE=6,则菱形的边长为( )
A.12 B.8 C.4 D.2
4.菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为( )
A.3:1 B.4:1 C.5:1 D.6:1
5.如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为 cm2.
6.若菱形的两条对角线的比为3:4,且周长为20cm,则它的一组对边的距离等于_________cm,它的面积等于________cm2.
7.在菱形ABCD中,AB=4,AB边上的高DE垂直平分边AB,则BD=_____,AC=_____.
8.如图,菱形ABCD中,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE
9.如图,已知菱形ABCD,AB=AE,且∠EAD=2∠EAB.求证:BE=AF
二 提高题
10. 菱形的周长为100cm,一条对角线长为14cm,它的面积是( )
A. 168cm2 B. 336cm2 C. 672cm2 D. 84cm2
11.如图,菱形ABCD中,E、F分别是边BC、CD上的点,△AEF是正三角形,若AB=AE,则∠C= .
12.如图,在矩形中,边的长为3,点,分别在,上,连接,,,.若四边形是菱形,且,求BC的长.
三 发展题
13.菱形ABCD和菱形BEFG中,∠A=∠GBE=120°,P是线段DF的中点,连接PG、PC.
(1)如图1,G在BC上,探究PG与PC的位置关系;
(2)将菱形BEGF绕点B旋转至如图2的位置,使C、B、E在同一直线上.(1)的结论还成立吗?请说明理由.
【教与学反思】
学习目标:1.了解菱形的概念及其与平行四边形的关系.
2.探索并证明菱形的性质定理.
3.应用菱形的性质定理解决相关计算或证明问题.
学习重点: 探索并证明菱形的性质定理.
学习难点:应用菱形的性质定理解决相关计算或证明问题.
【展示课导学】
独学 合学 展学
主题一:菱形的定义与性质 问题1 如果从边的角度,将平行四边形特殊化,让它有一组邻边相等,这个特殊的四边形叫什么呢 定义: 叫做菱形. 思考:菱形与平行四边形的区别与联系? 问题2 请剪出一个菱形并观察,菱形是轴对称图形吗 若是,指出它的对称轴. 问题3 根据剪纸的过程,猜想菱形的四边在数量上有什么关系 菱形的两对角线有什么关系 请证明你的猜想: 归纳:菱形的性质并用几何语言表示 (1)菱形的四条边都 . (2)菱形的两条对角线 . 几何语言: 主题二:菱形的性质应用 1.如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12cm,AC=6cm,求菱形的周长. 2.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2. 求(1)∠ABC的度数; (2)对角线AC、BD的长; (3)菱形ABCD的面积. 菱形的面积公式: . 主题三:拓展提升 如图,把△FEP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF= ,∠BAD=60°,且AB> (1)求∠EPF的度数;
(2)若AP=10,求AE+AF的值
A.两人小对子: 讨论菱形的定义,性质及其证明,明确菱形与平行四边形的区别与联系. 预时 5 分钟 B.四人互助组: 讨论菱形的性质应用,解决周长、面积等几何问题,明确菱形的面积计算公式. 预时 5 分钟 C.八人共同体: 讨论拓展提升的问题,做好预展. 预时 5 分钟 展示单元一:菱形的定义与性质 策略建议: 菱形的定义及与平行四边形的关系; 菱形的性质探索证明. 预时 5 分钟 展示单元二:菱形性质的应用 策略建议: 利用菱形的性质求线段、周长和面积. 预时5 分钟 展示单元三:拓展提升 策略建议: 预时 5 分钟
梳理小结 菱形的性质:边、角、对角线、对称性 菱形的计算:周长、面积 数学方法:类比
查学 根据下图填空: (1)已知菱形ABCD的周长是12cm,那么它的边长是 ______. (2)在菱形ABCD中,∠ABC=120 °,则∠BAC=_______. (3)菱形ABCD的两条对角线长分别为6cm和8cm,则菱形的边长是_______. (4)菱形的一个内角为120°,平分这个内角的对角线长为11cm,菱形的周长为______. (5)菱形的面积为64cm2,两条对角线的比为 1∶2 ,那么菱形最短的那条对角线长为_______.
想匆忙地完成一件事以期达到加快速度的目的,结果总是要失败的。-------伊索
【评学】 “日清过关”巩固提升三层级达标训练题
课题: 18.2.2菱形(1) 班级_______________ 姓名______________
一 基础题
1.菱形具有而矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线互相垂直 C.对角线相等 D.四个角都相等
2.如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M、N的坐标分别是 ( )
A.M(5,0),N(8,4) B.M(4,0),N(8,4)
C.M(5,0),N(7,4) D.M(4,0),N(7,4)
3.已知菱形ABCD中,AE⊥BC于E,若S菱形ABCD=24,且AE=6,则菱形的边长为( )
A.12 B.8 C.4 D.2
4.菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为( )
A.3:1 B.4:1 C.5:1 D.6:1
5.如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为 cm2.
6.若菱形的两条对角线的比为3:4,且周长为20cm,则它的一组对边的距离等于_________cm,它的面积等于________cm2.
7.在菱形ABCD中,AB=4,AB边上的高DE垂直平分边AB,则BD=_____,AC=_____.
8.如图,菱形ABCD中,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE
9.如图,已知菱形ABCD,AB=AE,且∠EAD=2∠EAB.求证:BE=AF
二 提高题
10. 菱形的周长为100cm,一条对角线长为14cm,它的面积是( )
A. 168cm2 B. 336cm2 C. 672cm2 D. 84cm2
11.如图,菱形ABCD中,E、F分别是边BC、CD上的点,△AEF是正三角形,若AB=AE,则∠C= .
12.如图,在矩形中,边的长为3,点,分别在,上,连接,,,.若四边形是菱形,且,求BC的长.
三 发展题
13.菱形ABCD和菱形BEFG中,∠A=∠GBE=120°,P是线段DF的中点,连接PG、PC.
(1)如图1,G在BC上,探究PG与PC的位置关系;
(2)将菱形BEGF绕点B旋转至如图2的位置,使C、B、E在同一直线上.(1)的结论还成立吗?请说明理由.
【教与学反思】
