12.1 全等三角形课件
文档属性
| 名称 | 12.1 全等三角形课件 |  | |
| 格式 | zip | ||
| 文件大小 | 993.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-13 14:32:41 | ||
图片预览




文档简介
课件38张PPT。全等三角形下列各组图形的形状与大小有什么特点?能够完全重合的图形叫做全等图形
(1)(2)(3)(4)形状和大小
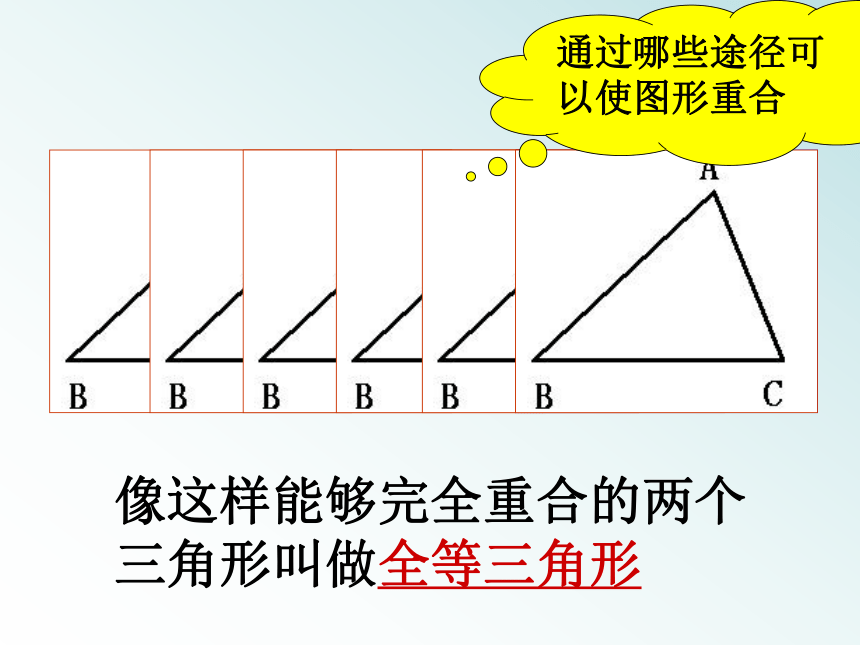
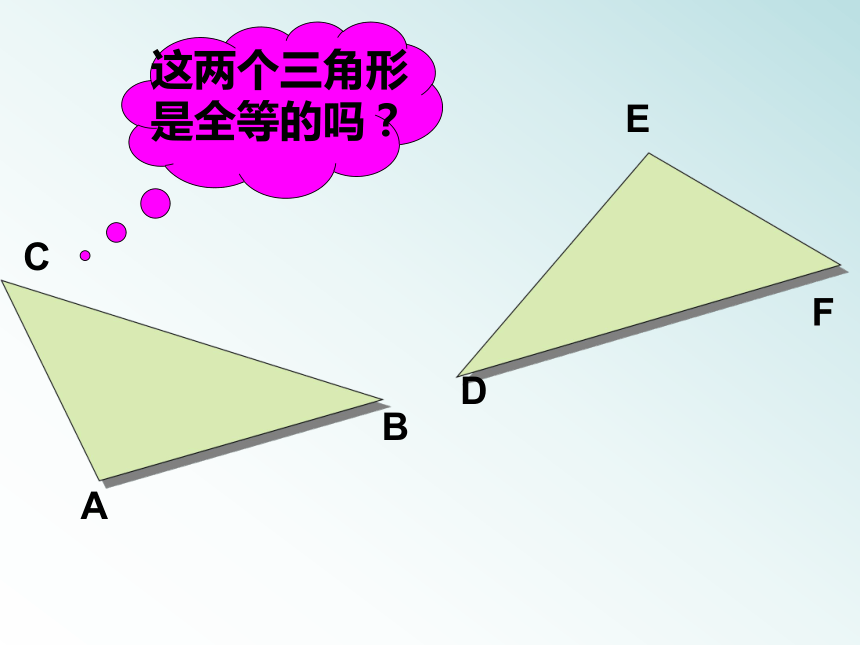
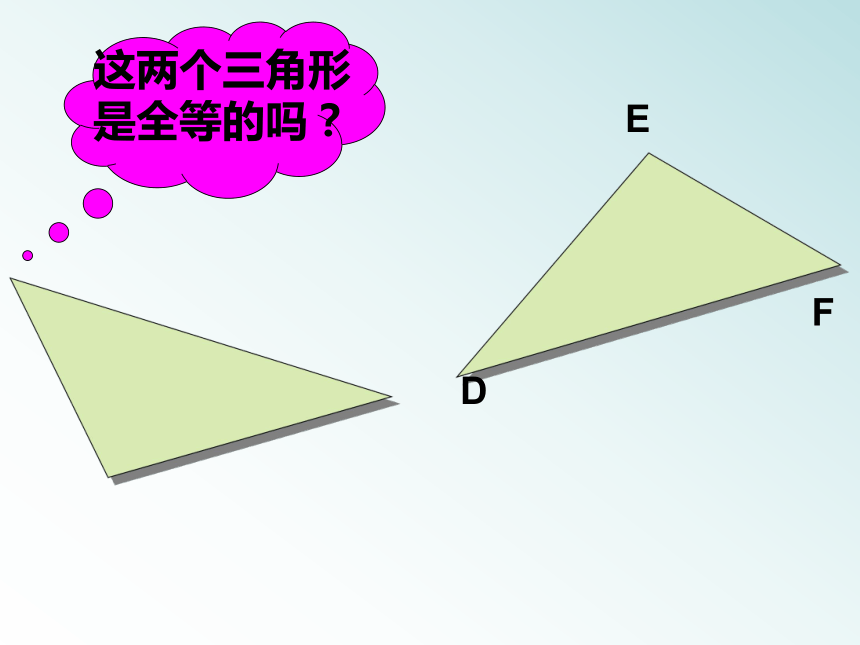
都相同形状不同大小不同像这样能够完全重合的两个三角形叫做全等三角形通过哪些途径可以使图形重合CABEDFEDF
通过哪些途径可以使图形重合翻折、平移、旋转是图形变换的三种形式。ABCA′B′C′lAABBCCA′A′B′B′C′(C′)图形经过翻折、平移、旋转后,位置发生了变化,但形状、大小不变。两个全等三角形重合时,
互相重合的顶点叫对应顶点,
互相重合的边叫做对应边,
互相重合的角叫做对应角。“全等”用符号“≌ ”表示记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。比如△ABC≌△DEF 读做“三角形ABC全等于三角形DEF”全等三角形的表示ABCA′B′C′ 记作:△ABC≌△A’B’C’,读作:△ABC全等于△A’B’C’A与A’对应顶点:B与B’ C与C’对应边:AB与A’B’CA与C’A’ BC与B’C’对应角:∠A与∠A’ ∠B与∠B’ ∠C与∠C’全等三角形的对应边相等,对应角相等。ABCDE△ABC≌△ADEABCDE△ABC≌△AED ABCDFE例2、如图,两个三角形是全等三角形。
请说出图中两个全等三角形通过何种运动可 以重合。并写出对应顶点、对应边、对应角。 ABCDEF△ABC≌△FDE ABCDEF△ABC≌△FDE两个全等三角形分别摆放成如图所示的位置,用符号来表示这两个全等三角形,并指出它们的对应顶点、对应边、对应角。全等三角形对应角所对的边是对应边,对应边所对的角是对应角。 ① ② ③1、若△AOC≌△BOD,对应
边是 ,对应角是 ;2、若△ABD≌△ACD,对应边是 ,对应角是 ;3、若△ABC≌△CDA,对应
边是 ,对应角是 ;问题二4、若△ABE≌△ACD,对应
边是 ,对应角是 ;观察上图,怎样正确找出全等三角形的对应边与对应角,有简便方法吗?思考(1)有公共边的,公共边是对应边;(2)有公共角的,公共角是对应角; (3)有对顶角的,对顶角是对应角(4)大对大,小对小; (大边对大边,小边对小边. 大角对大角,小角对小角) 问题三:运用规律找出下列图中一对 全等三角形的对应边、对应角。DCBADCBA 如图,已知△ABC≌△ADE,
∠C=∠E,BC=DE,其它的对应边
有 :_____________
对应角有:_____________
ABCDE找一找 两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论?观察与思考全等三角形的性质全等三角形的对应边相等全等三角形的对应角相等用途?条件和结论 ∵△ABC≌ △DFE 应用全等三角形的对应边相等全等三角形的对应角相等∴ AB=DF,
( )∴ ∠ A= ∠ D,
( )BC=FE, AC=DE∠ B= ∠ F , ∠ C= ∠ E4(1)、如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。456如图.已知△ABC≌△ADE。
求证:∠1= ∠2
能力提高 ·拓展、延伸:
已知△ABC≌△DFE, ∠ A=96o,∠B=25o,DF=10cm.求 ∠ E的度数及AB的长.解:∠ C=180o-∠ A -∠ B
= 180o- 96o- 25o
=59o
∵ △ABC≌△DFE
∴ ∠ E=∠ C=59o,AB=DF= 10cm
通过本堂课的学习,
你掌握了什么内容?
收获了哪些?感悟与反思
(1)(2)(3)(4)形状和大小
都相同形状不同大小不同像这样能够完全重合的两个三角形叫做全等三角形通过哪些途径可以使图形重合CABEDFEDF
通过哪些途径可以使图形重合翻折、平移、旋转是图形变换的三种形式。ABCA′B′C′lAABBCCA′A′B′B′C′(C′)图形经过翻折、平移、旋转后,位置发生了变化,但形状、大小不变。两个全等三角形重合时,
互相重合的顶点叫对应顶点,
互相重合的边叫做对应边,
互相重合的角叫做对应角。“全等”用符号“≌ ”表示记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。比如△ABC≌△DEF 读做“三角形ABC全等于三角形DEF”全等三角形的表示ABCA′B′C′ 记作:△ABC≌△A’B’C’,读作:△ABC全等于△A’B’C’A与A’对应顶点:B与B’ C与C’对应边:AB与A’B’CA与C’A’ BC与B’C’对应角:∠A与∠A’ ∠B与∠B’ ∠C与∠C’全等三角形的对应边相等,对应角相等。ABCDE△ABC≌△ADEABCDE△ABC≌△AED ABCDFE例2、如图,两个三角形是全等三角形。
请说出图中两个全等三角形通过何种运动可 以重合。并写出对应顶点、对应边、对应角。 ABCDEF△ABC≌△FDE ABCDEF△ABC≌△FDE两个全等三角形分别摆放成如图所示的位置,用符号来表示这两个全等三角形,并指出它们的对应顶点、对应边、对应角。全等三角形对应角所对的边是对应边,对应边所对的角是对应角。 ① ② ③1、若△AOC≌△BOD,对应
边是 ,对应角是 ;2、若△ABD≌△ACD,对应边是 ,对应角是 ;3、若△ABC≌△CDA,对应
边是 ,对应角是 ;问题二4、若△ABE≌△ACD,对应
边是 ,对应角是 ;观察上图,怎样正确找出全等三角形的对应边与对应角,有简便方法吗?思考(1)有公共边的,公共边是对应边;(2)有公共角的,公共角是对应角; (3)有对顶角的,对顶角是对应角(4)大对大,小对小; (大边对大边,小边对小边. 大角对大角,小角对小角) 问题三:运用规律找出下列图中一对 全等三角形的对应边、对应角。DCBADCBA 如图,已知△ABC≌△ADE,
∠C=∠E,BC=DE,其它的对应边
有 :_____________
对应角有:_____________
ABCDE找一找 两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论?观察与思考全等三角形的性质全等三角形的对应边相等全等三角形的对应角相等用途?条件和结论 ∵△ABC≌ △DFE 应用全等三角形的对应边相等全等三角形的对应角相等∴ AB=DF,
( )∴ ∠ A= ∠ D,
( )BC=FE, AC=DE∠ B= ∠ F , ∠ C= ∠ E4(1)、如图△ ABD ≌ △CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。456如图.已知△ABC≌△ADE。
求证:∠1= ∠2
能力提高 ·拓展、延伸:
已知△ABC≌△DFE, ∠ A=96o,∠B=25o,DF=10cm.求 ∠ E的度数及AB的长.解:∠ C=180o-∠ A -∠ B
= 180o- 96o- 25o
=59o
∵ △ABC≌△DFE
∴ ∠ E=∠ C=59o,AB=DF= 10cm
通过本堂课的学习,
你掌握了什么内容?
收获了哪些?感悟与反思
