直线和圆的位置关系与 切线判定定理[上学期]
文档属性
| 名称 | 直线和圆的位置关系与 切线判定定理[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 236.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-07-16 18:00:00 | ||
图片预览



文档简介
课件12张PPT。直线和圆的位置关系(2)
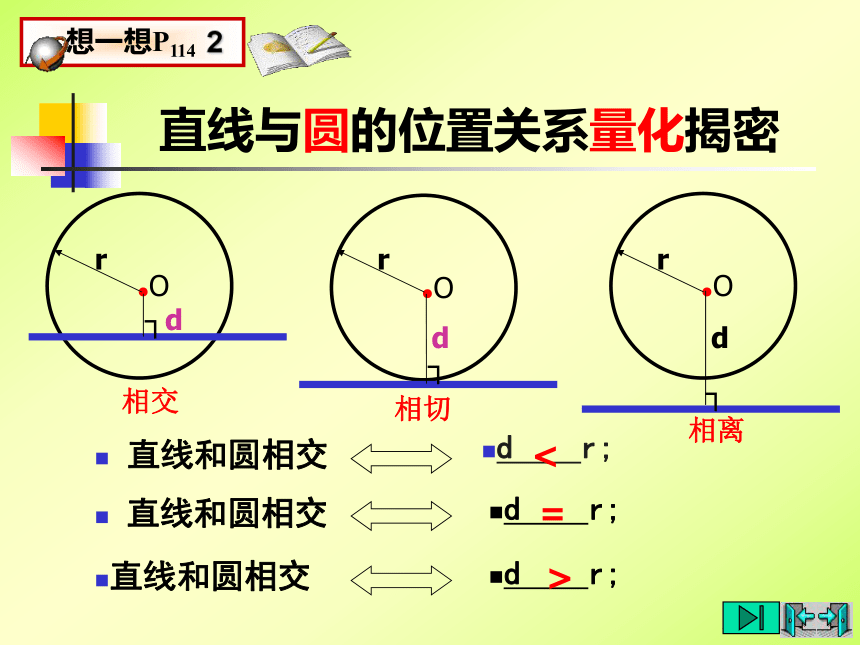
切线判定定理直线和圆相交d r;d r; 直线和圆相交直线和圆相交d r;直线与圆的位置关系量化揭密<=>切线的性质定理定理 圆切直线垂直于过切点的半径.如图∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.老师提示:
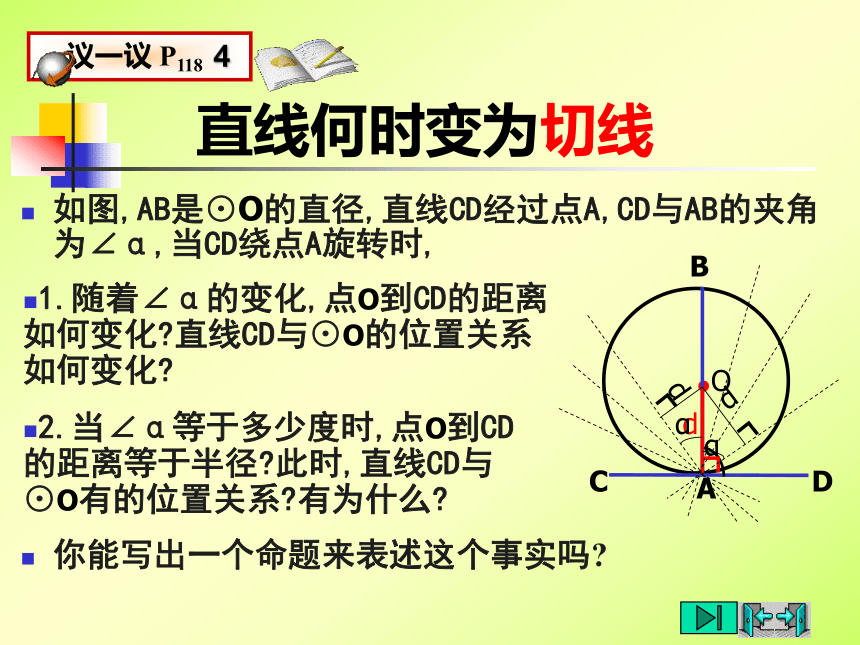
切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.老师提示:
切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
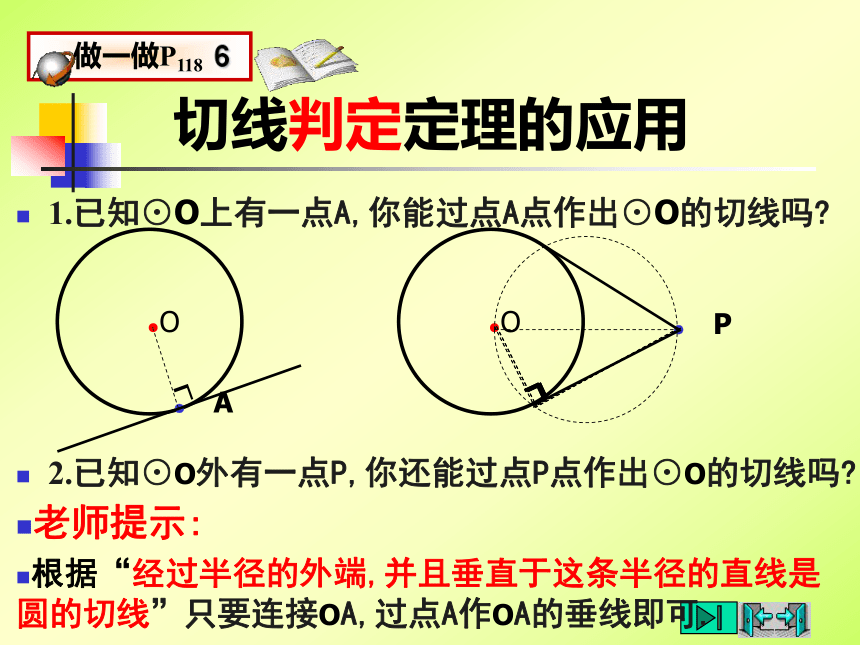
∴ CD是⊙O的切线.切线判定定理的应用1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?老师提示:
根据“经过半径的外端,并且垂直于这条半径的直线是圆的切线”只要连接OA,过点A作OA的垂线即可.2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?从一块三角形材料中,能否剪下一个圆,使其与各边都相切?老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.三角形与圆的位置关系I●I●这样的圆可以作出几个?为什么?.∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),∴因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.三角形与圆的位置关系三角形与圆的位置关系这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.老师提示:
多边形的边与圆的位置关系称为切.四边形与圆的位置关系如果四边形的四条边都与一个圆相切,这圆叫做四边形的内切圆.这个四边形叫做圆的外切四边形.我们可以证明圆外切四边的一个重要性质:
1.圆外切四边形两组对边的和相等.三角形与圆的“切”关系1.以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?.2.分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?老师提示:
先确定圆心和半径,尺规作图要保留作图痕迹.再见
切线判定定理直线和圆相交d r;d r; 直线和圆相交直线和圆相交d r;直线与圆的位置关系量化揭密<=>切线的性质定理定理 圆切直线垂直于过切点的半径.如图∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA.老师提示:
切线的性质定理是证明两线垂直的重要根据;作过切点的半径是常用经验辅助线之一.切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.老师提示:
切线的判定定理是证明一条直线是否是圆的切线的根据;作过切点的半径是常用经验辅助线之一.如图
∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,
∴ CD是⊙O的切线.切线判定定理的应用1.已知⊙O上有一点A,你能过点A点作出⊙O的切线吗?老师提示:
根据“经过半径的外端,并且垂直于这条半径的直线是圆的切线”只要连接OA,过点A作OA的垂线即可.2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?从一块三角形材料中,能否剪下一个圆,使其与各边都相切?老师提示:
假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.三角形与圆的位置关系I●I●这样的圆可以作出几个?为什么?.∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),∴因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.三角形与圆的位置关系三角形与圆的位置关系这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.老师提示:
多边形的边与圆的位置关系称为切.四边形与圆的位置关系如果四边形的四条边都与一个圆相切,这圆叫做四边形的内切圆.这个四边形叫做圆的外切四边形.我们可以证明圆外切四边的一个重要性质:
1.圆外切四边形两组对边的和相等.三角形与圆的“切”关系1.以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?.2.分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?老师提示:
先确定圆心和半径,尺规作图要保留作图痕迹.再见
