切线长定理[上学期]
图片预览




文档简介
课件18张PPT。切 线 长 定 理课 型:复习课
授课人:阚志强已知一条切线时,常有五个性质:
1、切线和圆只有一个公共点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线必过圆心。ABPO。切 线 长 定 理教 学 目 标
知识目标:
1、理解切线长定理,懂得定理的产生过程;
2、会灵活运用切线长定理探究一些结论,并应
用定理解题。
能力目标:
探求问题,寻求结论
重点:
切线长定理的应用
难点:
定理的探求、延伸
阅读课文
P118,
思考下列
问题:1、什么叫做圆外一点到圆的切线长?
2、切线长定理的内容是什么?
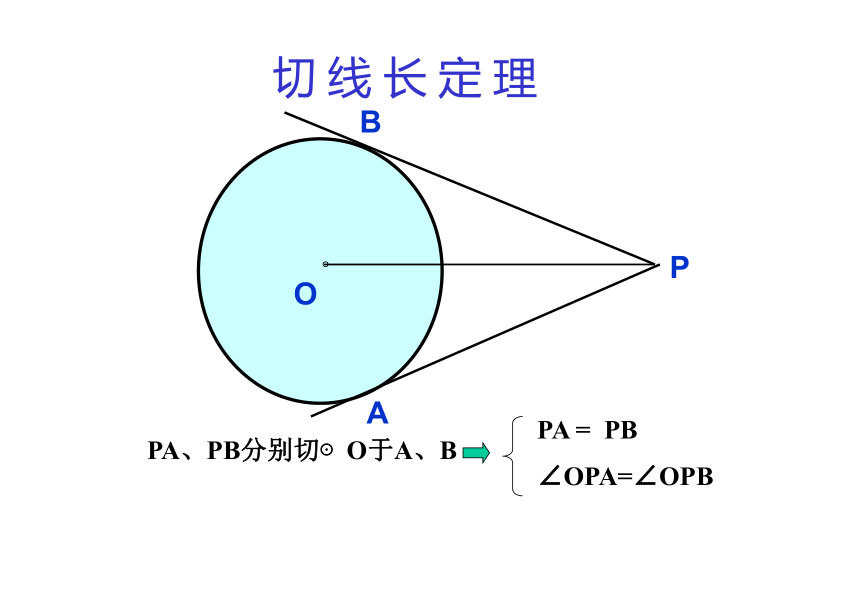
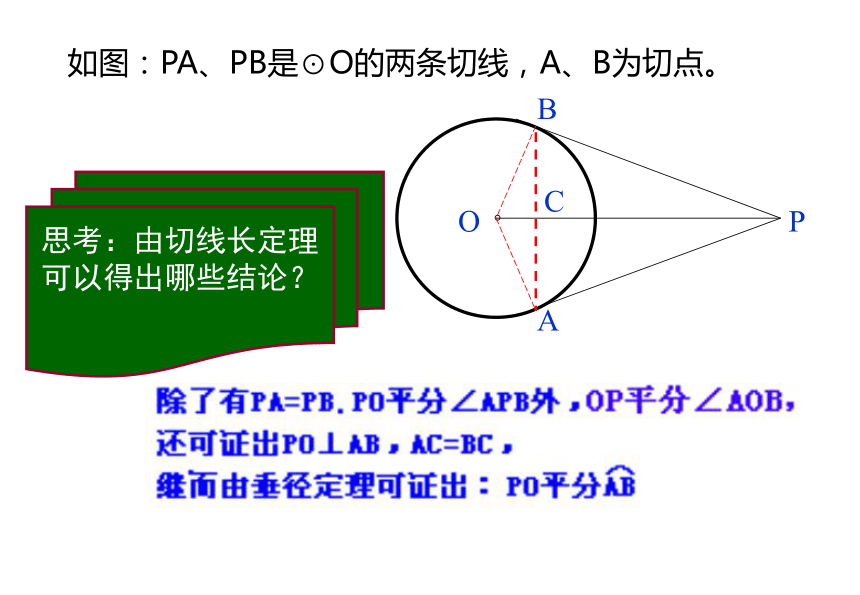
3、这个定理是怎样证明的?ABPO。切 线 长 定 理PA、PB分别切⊙O于A、BPA = PB∠OPA=∠OPB。PABOC如图:PA、PB是⊙O的两条切线,A、B为切点。思考:由切线长定理可以得出哪些结论?
若已知圆的三条切线呢?ABCDEF设△ABC的BC=a,CA=b,AB=c,内切圆I和BC、AC、AB分别相切于点D、E、F.Ixyzy+z=a
x+z=b
x+y=c分析:设 AF=x,BD=y,CE=z
已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。比一比
看谁做得快.ABCabcrr =a+b-c2例:直角三角形的两直角边分别是5cm,
12cm 则其内切圆的半径为______。DCEO如图:从⊙O外的定点P作⊙O
的两条切线,分别切⊙O于点A
和B,
⑵ ∠DOE的大小是定值 在弧AB上任取一点C,过
点C作⊙O的切线,分别交PA、
PB于点D、E。试证:⑴ △PDE的周长
是定值(PA+PB)(∠AOB/2)若∠P=40°,你能说出∠DOE的度数吗?BF如图:AE、BF分别切⊙O于A、B,且AE∥BF,EF切⊙O于C。试证:⑴ AB是⊙O的直径⑵ OE⊥OF ⑶ OC是AE、BF的比例中项⑷ 若⊙O 的半径为6,点C分半圆为1:2两部分,求AE、BF的长。
若以BF、BA所在的直线分别为x轴、y轴,B为原点,请求出EF所在直线的函数解析式。 xyBF⑷ 若⊙O 的半径为6,点C分半圆为1:2两部分,求AE、BF的长。
若以BF、BA所在的直线分别为x轴、y轴,B为原点,请求出EF所在直线的函数解析式。 xyD想一想圆的外切四边形具有什么性质?圆的外切四边形的两组对边的和相等。例:等腰梯形各边都与⊙O相切, ⊙O的直径为6cm,等腰梯形的腰等于8cm,则梯形的面积为_____。若已知圆的四条切线呢?868课堂小结通过这节课的复习,你有什么收获或体会?关于切线长定理,你还有什么不明白的问题?PABOPABCO达 标 检 测1、填空:已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙ O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。2、证明题:已知:如图,P为⊙ O外一点,PA、PB 为⊙ O 的切线,A和B是切点,BC是直径 求证:AC∥OP
60证明:连结AB
∵PA、PB分别切⊙O于A、B
∴PA=PB ∠OPA=∠OPB
∴OP⊥AB
又∵BC为⊙O的直径
∴AC⊥AB
∴AC∥OP作业: ⑴ P120 2 试证:点D是△PAB的内心
⑵ P120 3
胶南市隐珠中学认真 勤奋 拼搏 进取 欢迎您提出宝贵意见
授课人:阚志强已知一条切线时,常有五个性质:
1、切线和圆只有一个公共点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线必过圆心。ABPO。切 线 长 定 理教 学 目 标
知识目标:
1、理解切线长定理,懂得定理的产生过程;
2、会灵活运用切线长定理探究一些结论,并应
用定理解题。
能力目标:
探求问题,寻求结论
重点:
切线长定理的应用
难点:
定理的探求、延伸
阅读课文
P118,
思考下列
问题:1、什么叫做圆外一点到圆的切线长?
2、切线长定理的内容是什么?
3、这个定理是怎样证明的?ABPO。切 线 长 定 理PA、PB分别切⊙O于A、BPA = PB∠OPA=∠OPB。PABOC如图:PA、PB是⊙O的两条切线,A、B为切点。思考:由切线长定理可以得出哪些结论?
若已知圆的三条切线呢?ABCDEF设△ABC的BC=a,CA=b,AB=c,内切圆I和BC、AC、AB分别相切于点D、E、F.Ixyzy+z=a
x+z=b
x+y=c分析:设 AF=x,BD=y,CE=z
已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。比一比
看谁做得快.ABCabcrr =a+b-c2例:直角三角形的两直角边分别是5cm,
12cm 则其内切圆的半径为______。DCEO如图:从⊙O外的定点P作⊙O
的两条切线,分别切⊙O于点A
和B,
⑵ ∠DOE的大小是定值 在弧AB上任取一点C,过
点C作⊙O的切线,分别交PA、
PB于点D、E。试证:⑴ △PDE的周长
是定值(PA+PB)(∠AOB/2)若∠P=40°,你能说出∠DOE的度数吗?BF如图:AE、BF分别切⊙O于A、B,且AE∥BF,EF切⊙O于C。试证:⑴ AB是⊙O的直径⑵ OE⊥OF ⑶ OC是AE、BF的比例中项⑷ 若⊙O 的半径为6,点C分半圆为1:2两部分,求AE、BF的长。
若以BF、BA所在的直线分别为x轴、y轴,B为原点,请求出EF所在直线的函数解析式。 xyBF⑷ 若⊙O 的半径为6,点C分半圆为1:2两部分,求AE、BF的长。
若以BF、BA所在的直线分别为x轴、y轴,B为原点,请求出EF所在直线的函数解析式。 xyD想一想圆的外切四边形具有什么性质?圆的外切四边形的两组对边的和相等。例:等腰梯形各边都与⊙O相切, ⊙O的直径为6cm,等腰梯形的腰等于8cm,则梯形的面积为_____。若已知圆的四条切线呢?868课堂小结通过这节课的复习,你有什么收获或体会?关于切线长定理,你还有什么不明白的问题?PABOPABCO达 标 检 测1、填空:已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙ O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。2、证明题:已知:如图,P为⊙ O外一点,PA、PB 为⊙ O 的切线,A和B是切点,BC是直径 求证:AC∥OP
60证明:连结AB
∵PA、PB分别切⊙O于A、B
∴PA=PB ∠OPA=∠OPB
∴OP⊥AB
又∵BC为⊙O的直径
∴AC⊥AB
∴AC∥OP作业: ⑴ P120 2 试证:点D是△PAB的内心
⑵ P120 3
胶南市隐珠中学认真 勤奋 拼搏 进取 欢迎您提出宝贵意见
