切线2[上学期]
图片预览



文档简介
课件17张PPT。 切 线(2)一、教学目的 1.探索切线长定理,掌握切线长定理.
2.通过切线的识别和特征去发展学生逻辑思维能力.
3.通过创设情境和多种教学手段激发学生的学习兴趣,给学生创造成功的
机会,使他们乐于学习.?二、教学重点 切线长的定理 三、教学难点 四、教学方法 合作交流 五、教学用具 圆规,三角板 多媒体六、教学过程 切线长的定理的应用 1.直线与圆的三种位置关系
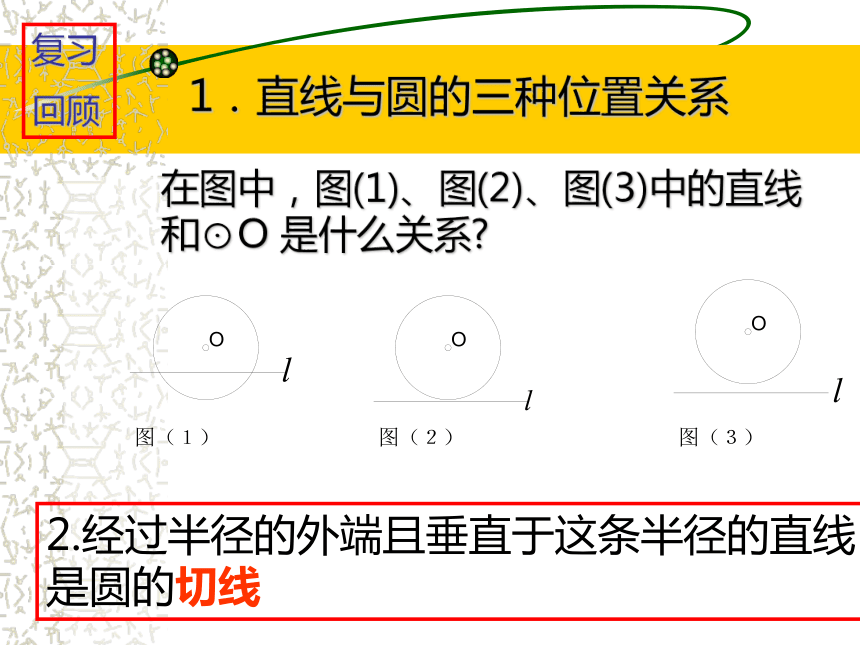
复习
回顾在图中,图(1)、图(2)、图(3)中的直线 和⊙O 是什么关系?2.经过半径的外端且垂直于这条半径的直线
是圆的切线 切线的判定方法有三种:3.切线的判定方法 ①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.复习
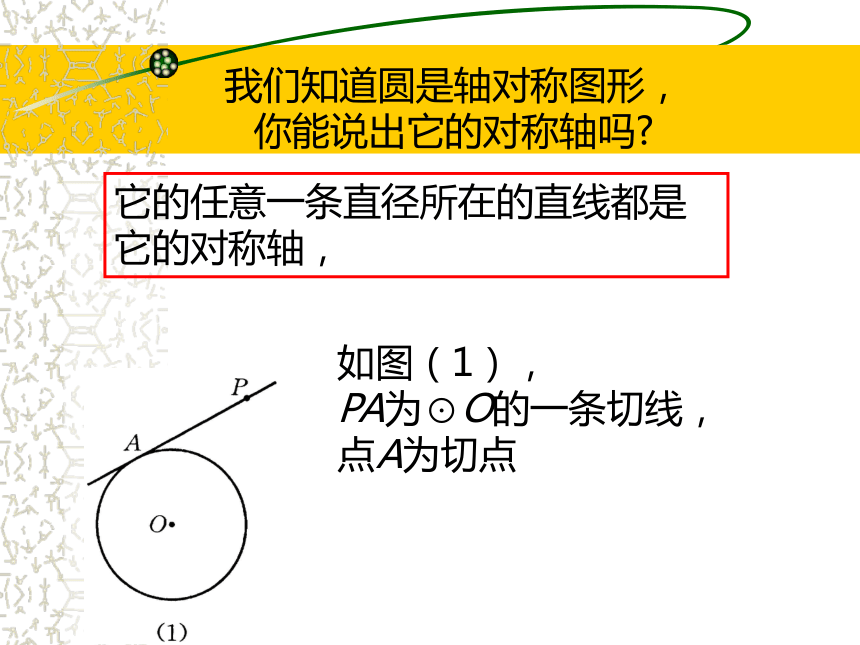
回顾我们知道圆是轴对称图形,
你能说出它的对称轴吗? 它的任意一条直径所在的直线都是
它的对称轴, 如图(1),
PA为⊙O的一条切线,
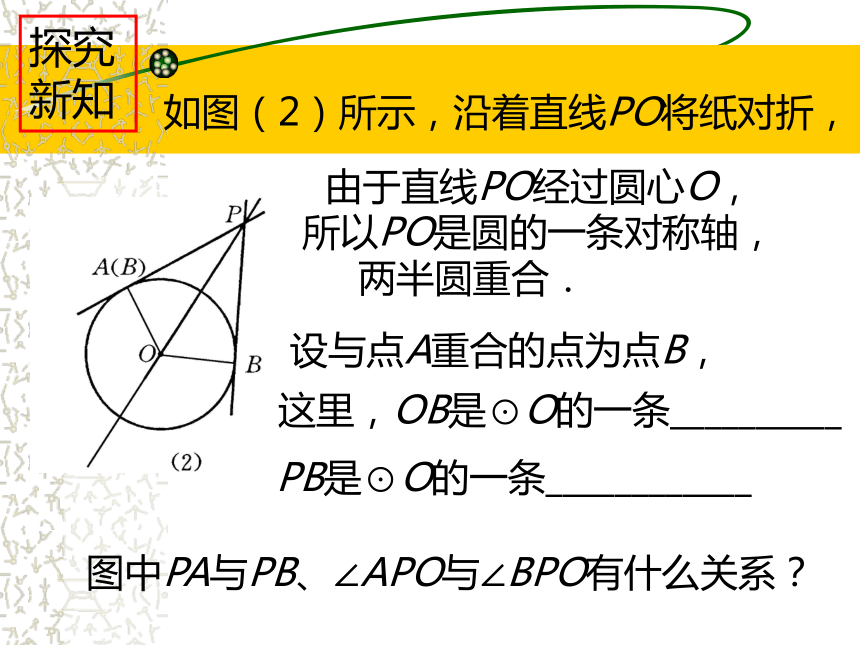
点A为切点 如图(2)所示,沿着直线PO将纸对折, 由于直线PO经过圆心O,
所以PO是圆的一条对称轴,
两半圆重合. . 设与点A重合的点为点B, 这里,OB是⊙O的一条__________ PB是⊙O的一条____________ 图中PA与PB、∠APO与∠BPO有什么关系?探究
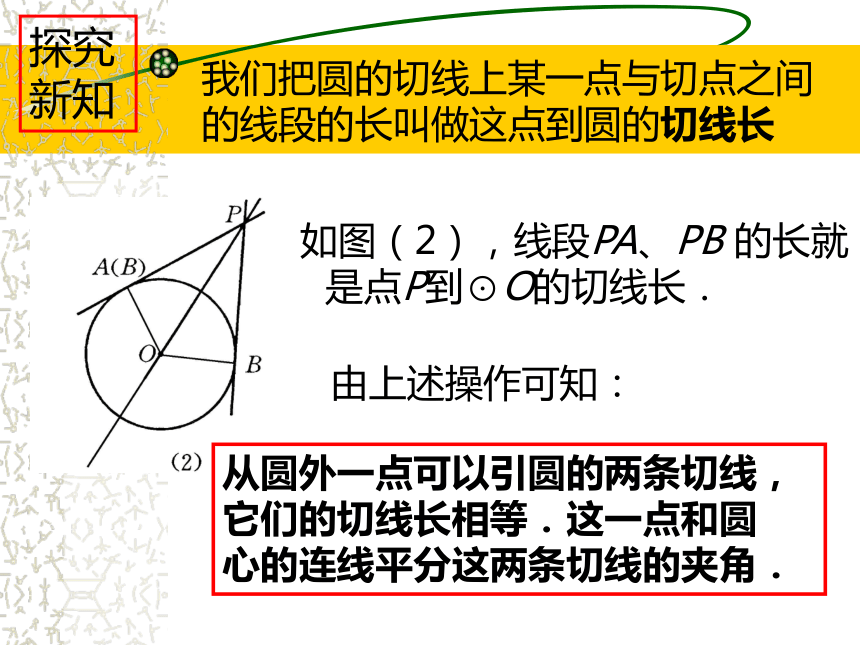
新知 我们把圆的切线上某一点与切点之间
的线段的长叫做这点到圆的切线长 如图(2),线段PA、PB 的长就
是点P到⊙O的切线长. .由上述操作可知: 从圆外一点可以引圆的两条切线,
它们的切线长相等.这一点和圆
心的连线平分这两条切线的夹角.探究
新知 试一试 如图23.2.11为一张三角形铁皮,如何
在它上面截一个面积最大的圆形铁皮?可能大家都会想到这样一个圆,
它与三角形的三条边都相切, 那么这样的圆存在吗? 我们又如何画出它来呢?如图,在△ABC中,如果有一圆与AB、AC、BC都相切,那么该圆的圆心到这三边的距离都等于半径.如何找到这个圆心呢?我们以前学过,角平分线上的
点到角的两边距离相等, 那么∠BAC 和∠ABC 平分线的
交点应该到三边的距离都相等.如果∠BAC 和∠ABC 的平分线
相交于点I, 那么点I到AC、AB、那么,以I为圆心,I到AB的距离为半径作圆,
则⊙I必与△ABC的三条边都相切.BC 的距离都相等.与三角形各边都相切的圆叫做三角形
的内切圆 三角形的内切圆的圆心叫做
三角形的内心 这个三角形叫做圆的
外切三角形 三角形的内心就是三角形三条
内角平分线的交点 1.图中等腰三角形、直角三角形个数分别是多少? 应用
拓展 2.已知⊿ABC的内切圆O与各边相切于D、E、F,那么点O是⊿DEF的 .三条中线的交点
三条高的交点
三条平分线的交点
三条边的垂直平分线的交点一处
两处
三处
四处3.直线l1、l2、l3表示三条相互交叉的公路,
现要建一个货物中转站,要求它到三条公路
的距离相等,则可供选择的地址有:4.在△ABC中,∠ABC =500, ∠ACB=750, 点O是内心, 求∠BOC的度数.5. 在△ABC中, ∠BAC=550, 点O是内心,
求∠BOC的度数 .6.⊙O是△ABC 的内切圆, 与AB、BC、CA分别切于点D、E、F, ∠DOE=120°, ∠EOF=150°, 求△ABC 的三个内角的度数.7. △ABC 的内切圆⊙O 与AC、AB、BC分别相切于点D、E、F,且AB=5厘米, BC=9厘米, AC=6厘米, 求AE、BF和CD的长.8. 设△ABC 的内切圆的半径为r, △ABC 的周长为 , 求△ABC 的面积S. 小 结1、切线长定理.2、三角形的内切圆 ,圆的外切三角形3.三角形的内心三角形的内心就是三角形
三条内角平分线的交点 教材第58页练习第1、2、3、4题 作业
2.通过切线的识别和特征去发展学生逻辑思维能力.
3.通过创设情境和多种教学手段激发学生的学习兴趣,给学生创造成功的
机会,使他们乐于学习.?二、教学重点 切线长的定理 三、教学难点 四、教学方法 合作交流 五、教学用具 圆规,三角板 多媒体六、教学过程 切线长的定理的应用 1.直线与圆的三种位置关系
复习
回顾在图中,图(1)、图(2)、图(3)中的直线 和⊙O 是什么关系?2.经过半径的外端且垂直于这条半径的直线
是圆的切线 切线的判定方法有三种:3.切线的判定方法 ①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理.复习
回顾我们知道圆是轴对称图形,
你能说出它的对称轴吗? 它的任意一条直径所在的直线都是
它的对称轴, 如图(1),
PA为⊙O的一条切线,
点A为切点 如图(2)所示,沿着直线PO将纸对折, 由于直线PO经过圆心O,
所以PO是圆的一条对称轴,
两半圆重合. . 设与点A重合的点为点B, 这里,OB是⊙O的一条__________ PB是⊙O的一条____________ 图中PA与PB、∠APO与∠BPO有什么关系?探究
新知 我们把圆的切线上某一点与切点之间
的线段的长叫做这点到圆的切线长 如图(2),线段PA、PB 的长就
是点P到⊙O的切线长. .由上述操作可知: 从圆外一点可以引圆的两条切线,
它们的切线长相等.这一点和圆
心的连线平分这两条切线的夹角.探究
新知 试一试 如图23.2.11为一张三角形铁皮,如何
在它上面截一个面积最大的圆形铁皮?可能大家都会想到这样一个圆,
它与三角形的三条边都相切, 那么这样的圆存在吗? 我们又如何画出它来呢?如图,在△ABC中,如果有一圆与AB、AC、BC都相切,那么该圆的圆心到这三边的距离都等于半径.如何找到这个圆心呢?我们以前学过,角平分线上的
点到角的两边距离相等, 那么∠BAC 和∠ABC 平分线的
交点应该到三边的距离都相等.如果∠BAC 和∠ABC 的平分线
相交于点I, 那么点I到AC、AB、那么,以I为圆心,I到AB的距离为半径作圆,
则⊙I必与△ABC的三条边都相切.BC 的距离都相等.与三角形各边都相切的圆叫做三角形
的内切圆 三角形的内切圆的圆心叫做
三角形的内心 这个三角形叫做圆的
外切三角形 三角形的内心就是三角形三条
内角平分线的交点 1.图中等腰三角形、直角三角形个数分别是多少? 应用
拓展 2.已知⊿ABC的内切圆O与各边相切于D、E、F,那么点O是⊿DEF的 .三条中线的交点
三条高的交点
三条平分线的交点
三条边的垂直平分线的交点一处
两处
三处
四处3.直线l1、l2、l3表示三条相互交叉的公路,
现要建一个货物中转站,要求它到三条公路
的距离相等,则可供选择的地址有:4.在△ABC中,∠ABC =500, ∠ACB=750, 点O是内心, 求∠BOC的度数.5. 在△ABC中, ∠BAC=550, 点O是内心,
求∠BOC的度数 .6.⊙O是△ABC 的内切圆, 与AB、BC、CA分别切于点D、E、F, ∠DOE=120°, ∠EOF=150°, 求△ABC 的三个内角的度数.7. △ABC 的内切圆⊙O 与AC、AB、BC分别相切于点D、E、F,且AB=5厘米, BC=9厘米, AC=6厘米, 求AE、BF和CD的长.8. 设△ABC 的内切圆的半径为r, △ABC 的周长为 , 求△ABC 的面积S. 小 结1、切线长定理.2、三角形的内切圆 ,圆的外切三角形3.三角形的内心三角形的内心就是三角形
三条内角平分线的交点 教材第58页练习第1、2、3、4题 作业
