切线[上学期]
图片预览



文档简介
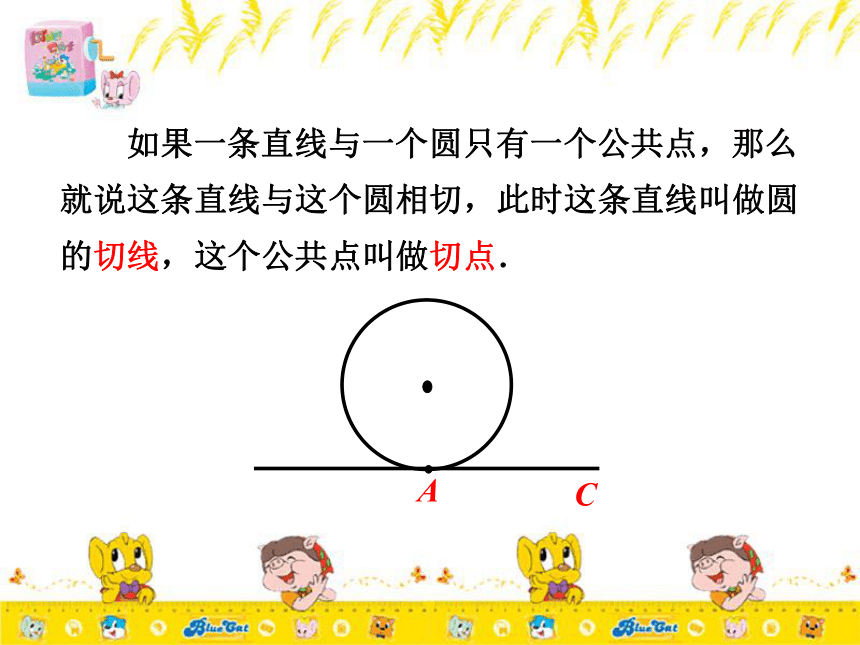
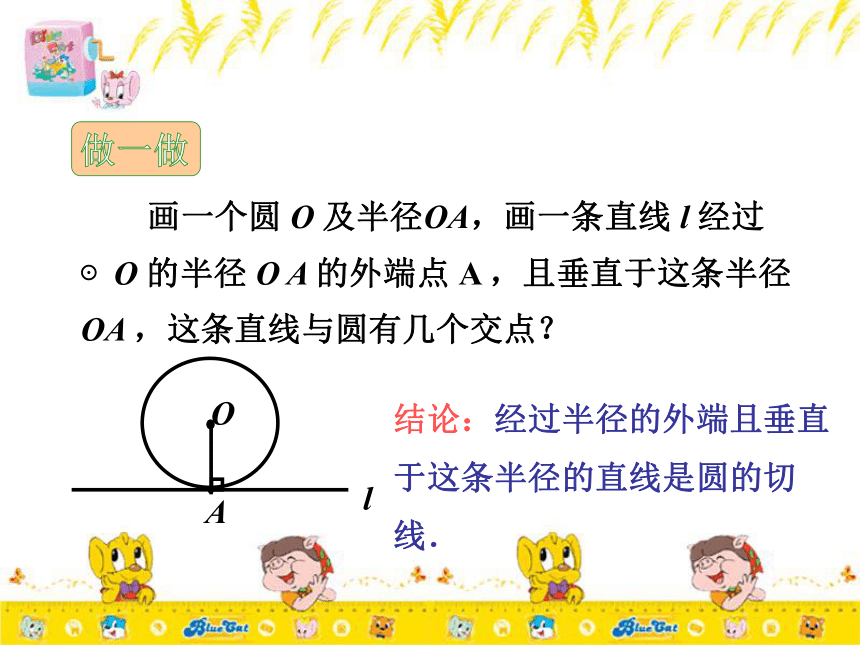
课件23张PPT。切 线授课老师:余先涛华师大版初三数学 如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆相切,此时这条直线叫做圆的切线,这个公共点叫做切点. 画一个圆 O 及半径OA,画一条直线 l 经过⊙O 的半径 O A 的外端点 A ,且垂直于这条半径OA ,这条直线与圆有几个交点? 结论:经过半径的外端且垂直
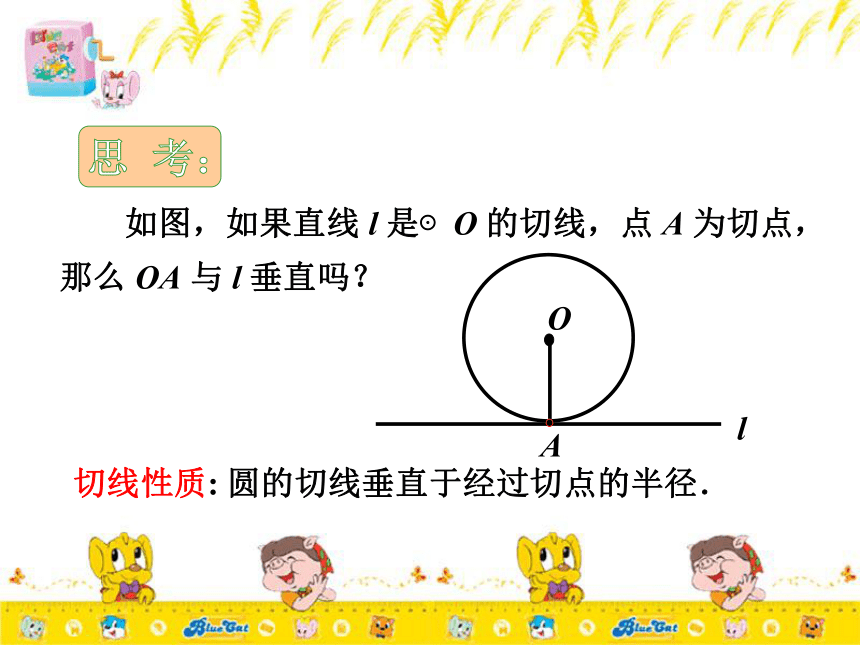
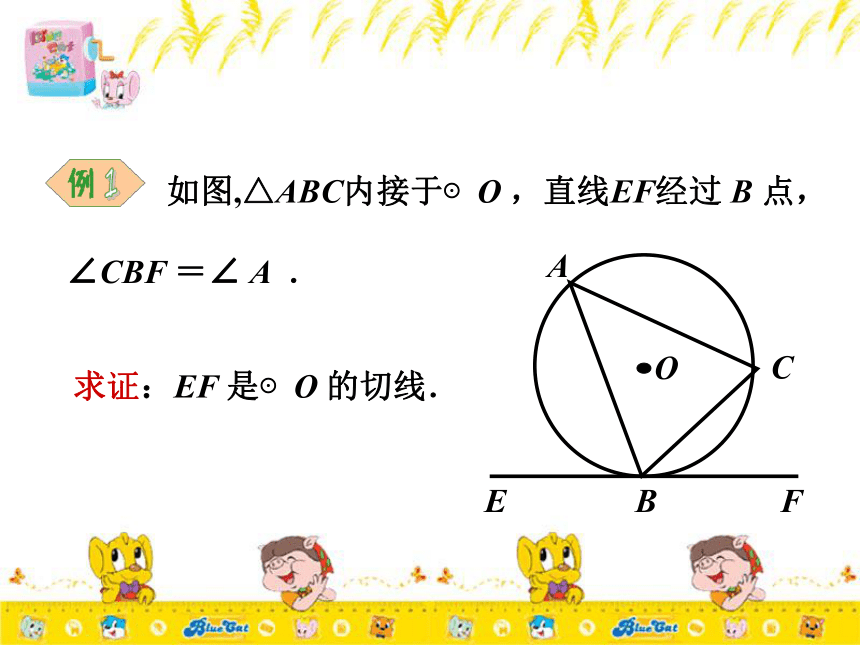
于这条半径的直线是圆的切线.判断一条直线是一个圆的切线有两个方法:1、判断这条直线是否经过已知圆的半径的外端 并且垂直于这条半径.2、判断圆心到这条直线的距离是否等于半径. 如图,如果直线 l 是⊙O 的切线,点 A 为切点,那么 OA 与 l 垂直吗?切线性质: 圆的切线垂直于经过切点的半径. 如图,△ABC内接于⊙O ,直线EF经过 B 点,
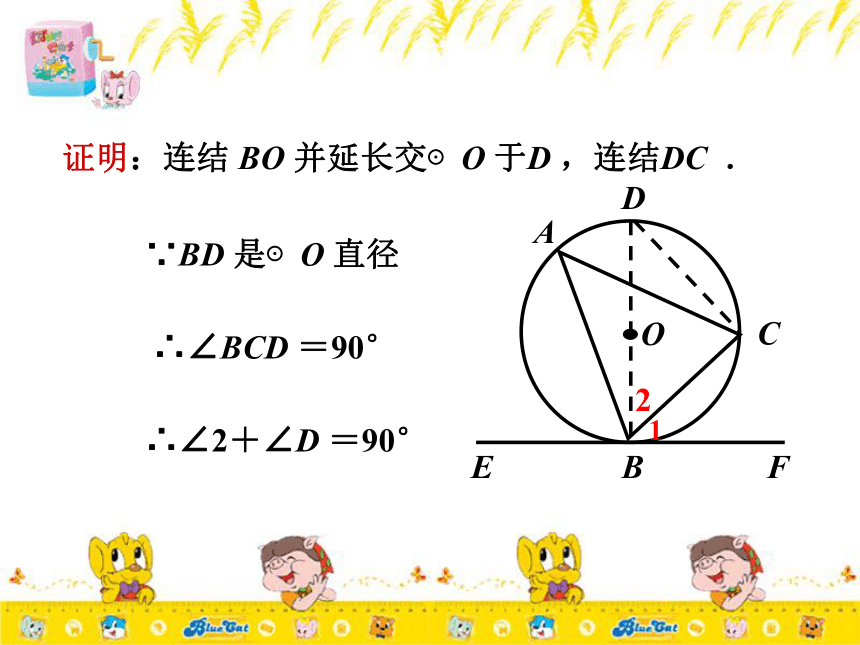
∠CBF =∠ A .求证:EF 是⊙O 的切线.1∵BD 是⊙O 直径 证明:连结 BO 并延长交⊙O 于D ,连结DC .∴∠2+∠D =90° ∴∠BCD =90° EFB12OCDA又∵∠D =∠A ∠A =∠CBF∴∠D =∠CBF∴DB ⊥ EF ∴EF 是⊙O 的切线.∴∠2+∠1=90 ° 如图,△ABC 中,AB =AC ,O 是BC 中点,
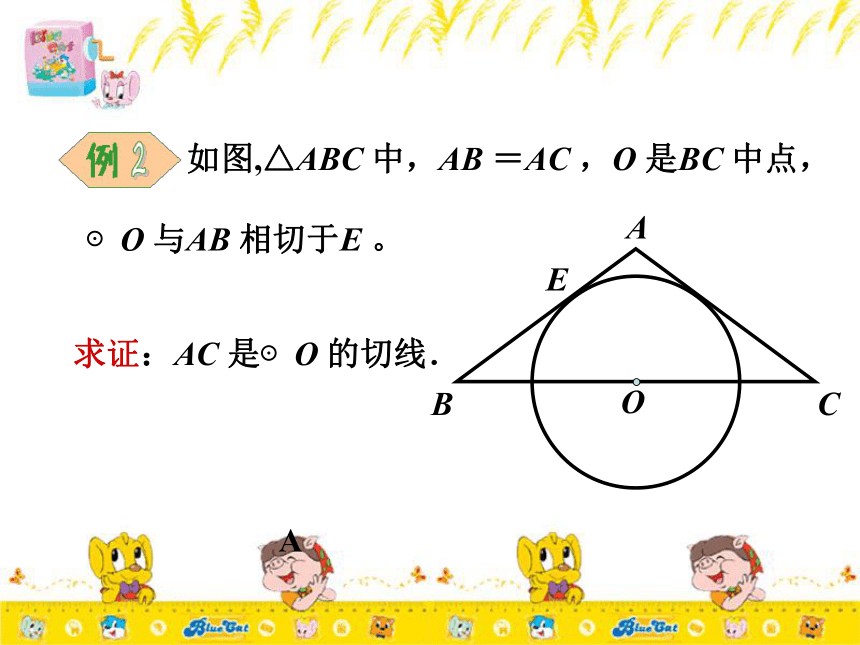
⊙O 与AB 相切于E 。2求证:AC 是⊙O 的切线. ABOCEA证明:连结OE ,OA, 过O 作OF ⊥AC∵⊙O 与AB 相切于E ∴OE ⊥ AB又∵△ABC 中,AB =AC ,
O 是BC 中点.∴AO 平分∠BACFBOCEA又OE ⊥AB ,OF⊥AC∴OE =OF∵OE 是⊙O 半径,OF =OE,OF ⊥ AC∴AC 是⊙O 的切线. 如图,PA 为⊙O 的一条切线,点A 为切点,沿着直线PO 将纸对折,由于直线PO 经过圆心O .所以PO 是圆的一条对称轴,两半圆重合,设与点 A 重合的点为点 B ,这里OB 与⊙O有什么关系,图中PA 与PB ,∠APO 与∠BPO 有什么关系? OAP 我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长. 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角. 切线长定理: ∵ PA、PB 分别切⊙O 于点A 、B∴ PA =PB∠APO =∠BPO 如图,一张三角形铁皮,如何在它上面截一个面积最大的圆形铁皮? 与三角形各边都相切的圆叫做三角形的内切圆,三角形内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形,三角形的内心就是三角形三条内角平分线的交点. 3 △ABC 的内切圆⊙O 与AC 、AB 、BC 分别相切于D 、E 、F ,且AB =5厘米,BC =9cm ,AC=8cm ,求AE、BF和CD的长. O。分析:设AE =x BF =y ,CD =z根据切线长定理,AD =x BE =y CF =z Rt△ABC 的两条直角边长分别为5和12,
则△ABC 的内切圆的半径为多少?4又 AB =13 , ∴5-r+12-r=13, r =2.分析:由勾股定理AB =13 .设△ABC 内切圆半径为r .则OD =r , OE =r∴DC =r , CE =r∴AD =5-r =AF , BE =12-r =BFa - r + b - r=c一般地∴分析:∵∠ABC+∠ACB =180°-∠A∴∠1+∠2= (180°-∠A)=90°- ∠A∴∠BIC =180°-(90°- ∠A)
=90°+ ∠A5 在△ABC 中,I 为内心,
探索∠A 与∠BIC 的关系?
于这条半径的直线是圆的切线.判断一条直线是一个圆的切线有两个方法:1、判断这条直线是否经过已知圆的半径的外端 并且垂直于这条半径.2、判断圆心到这条直线的距离是否等于半径. 如图,如果直线 l 是⊙O 的切线,点 A 为切点,那么 OA 与 l 垂直吗?切线性质: 圆的切线垂直于经过切点的半径. 如图,△ABC内接于⊙O ,直线EF经过 B 点,
∠CBF =∠ A .求证:EF 是⊙O 的切线.1∵BD 是⊙O 直径 证明:连结 BO 并延长交⊙O 于D ,连结DC .∴∠2+∠D =90° ∴∠BCD =90° EFB12OCDA又∵∠D =∠A ∠A =∠CBF∴∠D =∠CBF∴DB ⊥ EF ∴EF 是⊙O 的切线.∴∠2+∠1=90 ° 如图,△ABC 中,AB =AC ,O 是BC 中点,
⊙O 与AB 相切于E 。2求证:AC 是⊙O 的切线. ABOCEA证明:连结OE ,OA, 过O 作OF ⊥AC∵⊙O 与AB 相切于E ∴OE ⊥ AB又∵△ABC 中,AB =AC ,
O 是BC 中点.∴AO 平分∠BACFBOCEA又OE ⊥AB ,OF⊥AC∴OE =OF∵OE 是⊙O 半径,OF =OE,OF ⊥ AC∴AC 是⊙O 的切线. 如图,PA 为⊙O 的一条切线,点A 为切点,沿着直线PO 将纸对折,由于直线PO 经过圆心O .所以PO 是圆的一条对称轴,两半圆重合,设与点 A 重合的点为点 B ,这里OB 与⊙O有什么关系,图中PA 与PB ,∠APO 与∠BPO 有什么关系? OAP 我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长. 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角. 切线长定理: ∵ PA、PB 分别切⊙O 于点A 、B∴ PA =PB∠APO =∠BPO 如图,一张三角形铁皮,如何在它上面截一个面积最大的圆形铁皮? 与三角形各边都相切的圆叫做三角形的内切圆,三角形内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形,三角形的内心就是三角形三条内角平分线的交点. 3 △ABC 的内切圆⊙O 与AC 、AB 、BC 分别相切于D 、E 、F ,且AB =5厘米,BC =9cm ,AC=8cm ,求AE、BF和CD的长. O。分析:设AE =x BF =y ,CD =z根据切线长定理,AD =x BE =y CF =z Rt△ABC 的两条直角边长分别为5和12,
则△ABC 的内切圆的半径为多少?4又 AB =13 , ∴5-r+12-r=13, r =2.分析:由勾股定理AB =13 .设△ABC 内切圆半径为r .则OD =r , OE =r∴DC =r , CE =r∴AD =5-r =AF , BE =12-r =BFa - r + b - r=c一般地∴分析:∵∠ABC+∠ACB =180°-∠A∴∠1+∠2= (180°-∠A)=90°- ∠A∴∠BIC =180°-(90°- ∠A)
=90°+ ∠A5 在△ABC 中,I 为内心,
探索∠A 与∠BIC 的关系?
