切线[下学期]
图片预览



文档简介
课件14张PPT。切线探究1:
画一个圆O及半径OA,画一条直线l经过圆O的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?想一想:
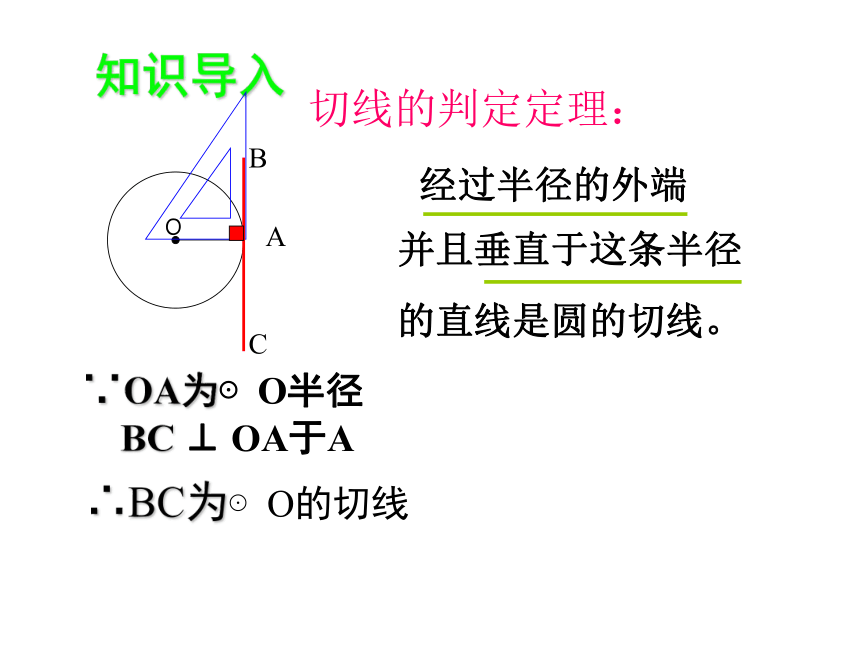
满足什么条件的直线是圆的切线?OAl知识导入BC经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定定理:∵OA为⊙O半径BC ⊥ OA于A∴BC为⊙O的切线判断:
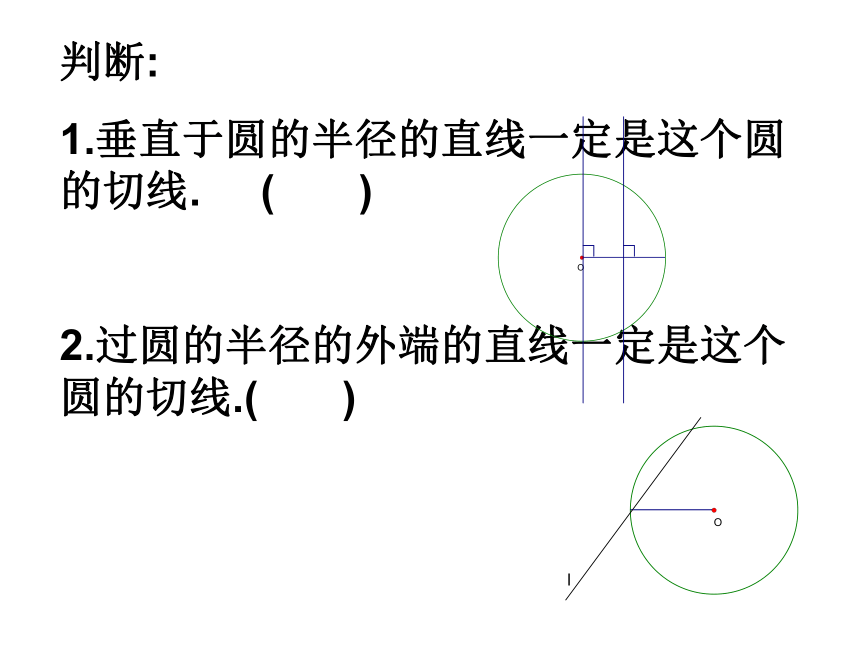
1.垂直于圆的半径的直线一定是这个圆的切线. ( )
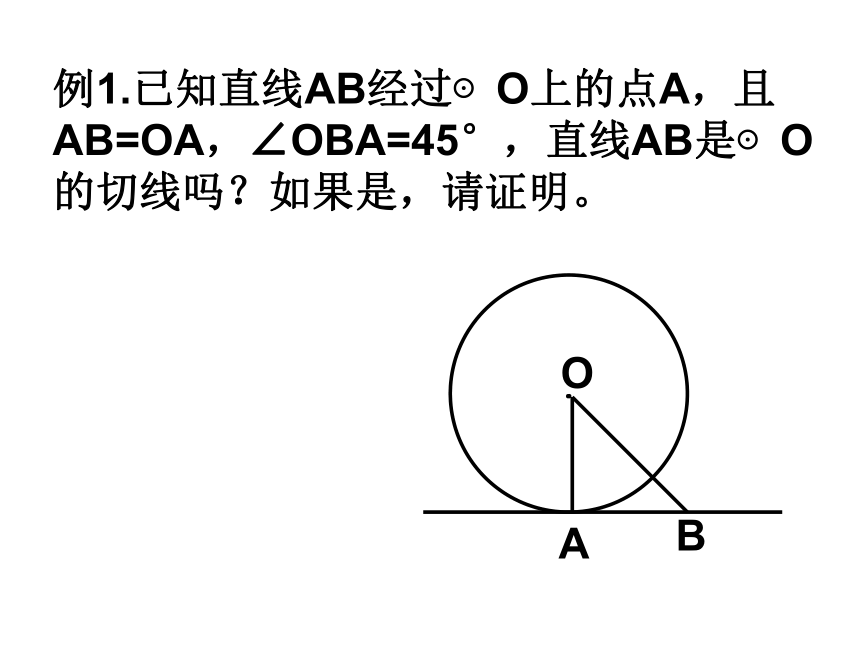
2.过圆的半径的外端的直线一定是这个圆的切线.( )判定一条直线是圆的切线的三种方法 1、利用定义:与圆有唯一公共点的直线是圆的切线。2、利用定理:与圆心距离等于圆的半径的直线是圆的切线。3、利用切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线。例1.已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?如果是,请证明。OAB练习
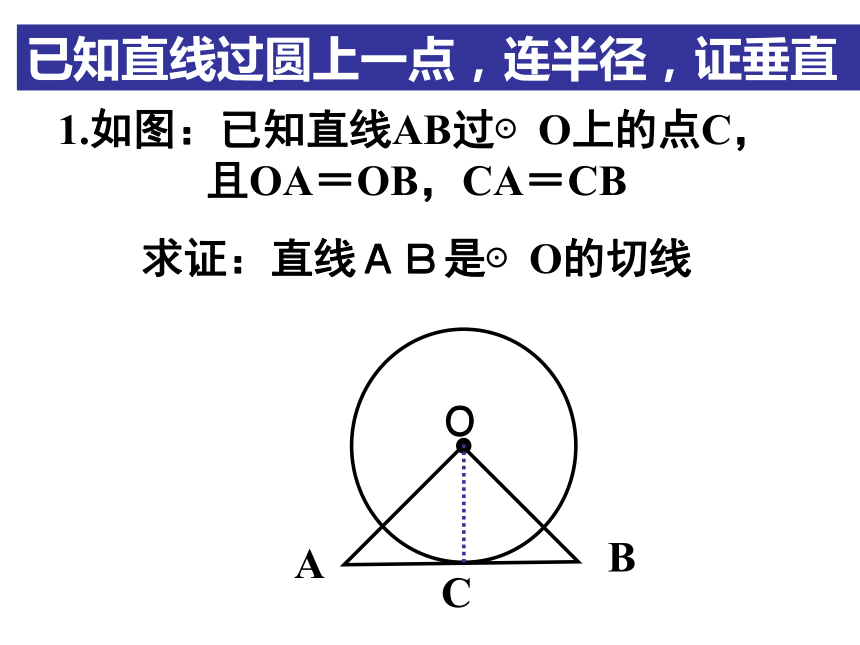
1.如图:已知直线AB过⊙O上的点C,且OA=OB,CA=CB
求证:直线AB是⊙O的切线BO
AC已知直线过圆上一点,连半径,证垂直2.如图,A是⊙O外的一点,AO的延长线交⊙O于C,直线AB经过⊙O上一点B,且AB=BC,∠C=30o。
求证:直线AB是⊙O的切线。已知直线过圆上一点,连半径,证垂直3.如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC是⊙O 的切线。CO
ABDE未知直线过圆上一点,作垂直,证半径探究2.
如图,如果直线l是⊙O的切线,点A是切点,那么半径OA与l垂直吗?OAl切线的性质定理: 圆的切线垂直于过切点的半径.∵l是⊙O切线 OA是半径∴OA⊥l例:如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点. 求证:C是AB的中点.ABCO已知切线,连圆心与切点,得垂直练习:1. 如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.1OBACDOADCB123已知切线,连圆心与切点,得垂直2.如图,已知⊿ABC为等腰三角形,O是底边BC的中点, ⊙O与腰AB相切于点D. 证明:AC与⊙O相切.ACOBDE已知切线,连圆心与切点,得垂直未知直线过圆上一点,作垂直,证半径本讲着重介绍了“切线的判定定理”利用此定理判定一条直线是否为 圆的切线时,必须注意直线是否符合题设的两个条件,二者缺一不可, 如图(1)中的直线l虽过⊙O的半径外端A,但与⊙O有两个交点,不是⊙ O的切线,又如图(2)中的直线l虽与半径OA垂直,但它与⊙O无公共点, 故也不是⊙O的切线。 ?? 要判定一条直线是圆的切线,我们已学过三种方法,如下表所示:
小结要判定一条直线是圆的切线,我们已学过三种方法,如下表所示:今天,你有哪些收获?已知直线过圆上一点,连半径,证垂直未知直线过圆上一点,作垂直,证半径已知切线,连圆心与切点,得垂直
画一个圆O及半径OA,画一条直线l经过圆O的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?想一想:
满足什么条件的直线是圆的切线?OAl知识导入BC经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定定理:∵OA为⊙O半径BC ⊥ OA于A∴BC为⊙O的切线判断:
1.垂直于圆的半径的直线一定是这个圆的切线. ( )
2.过圆的半径的外端的直线一定是这个圆的切线.( )判定一条直线是圆的切线的三种方法 1、利用定义:与圆有唯一公共点的直线是圆的切线。2、利用定理:与圆心距离等于圆的半径的直线是圆的切线。3、利用切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线。例1.已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?如果是,请证明。OAB练习
1.如图:已知直线AB过⊙O上的点C,且OA=OB,CA=CB
求证:直线AB是⊙O的切线BO
AC已知直线过圆上一点,连半径,证垂直2.如图,A是⊙O外的一点,AO的延长线交⊙O于C,直线AB经过⊙O上一点B,且AB=BC,∠C=30o。
求证:直线AB是⊙O的切线。已知直线过圆上一点,连半径,证垂直3.如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC是⊙O 的切线。CO
ABDE未知直线过圆上一点,作垂直,证半径探究2.
如图,如果直线l是⊙O的切线,点A是切点,那么半径OA与l垂直吗?OAl切线的性质定理: 圆的切线垂直于过切点的半径.∵l是⊙O切线 OA是半径∴OA⊥l例:如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点. 求证:C是AB的中点.ABCO已知切线,连圆心与切点,得垂直练习:1. 如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.1OBACDOADCB123已知切线,连圆心与切点,得垂直2.如图,已知⊿ABC为等腰三角形,O是底边BC的中点, ⊙O与腰AB相切于点D. 证明:AC与⊙O相切.ACOBDE已知切线,连圆心与切点,得垂直未知直线过圆上一点,作垂直,证半径本讲着重介绍了“切线的判定定理”利用此定理判定一条直线是否为 圆的切线时,必须注意直线是否符合题设的两个条件,二者缺一不可, 如图(1)中的直线l虽过⊙O的半径外端A,但与⊙O有两个交点,不是⊙ O的切线,又如图(2)中的直线l虽与半径OA垂直,但它与⊙O无公共点, 故也不是⊙O的切线。 ?? 要判定一条直线是圆的切线,我们已学过三种方法,如下表所示:
小结要判定一条直线是圆的切线,我们已学过三种方法,如下表所示:今天,你有哪些收获?已知直线过圆上一点,连半径,证垂直未知直线过圆上一点,作垂直,证半径已知切线,连圆心与切点,得垂直
