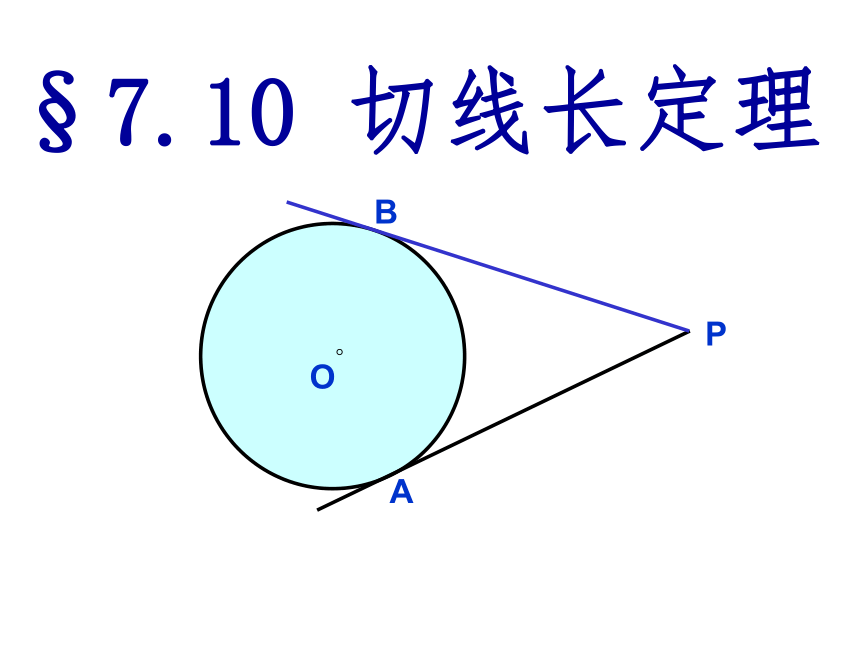
切线[上学期]
图片预览


文档简介
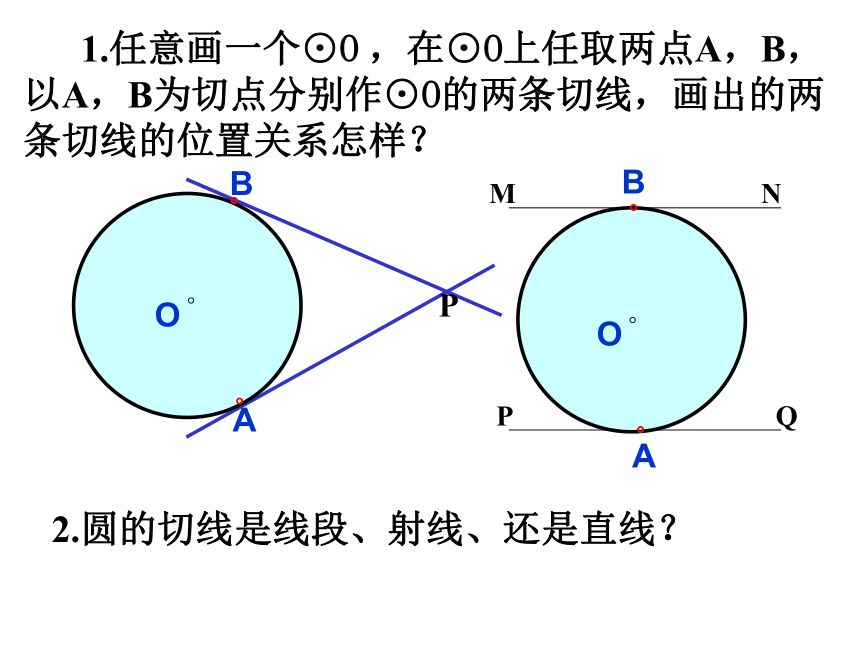
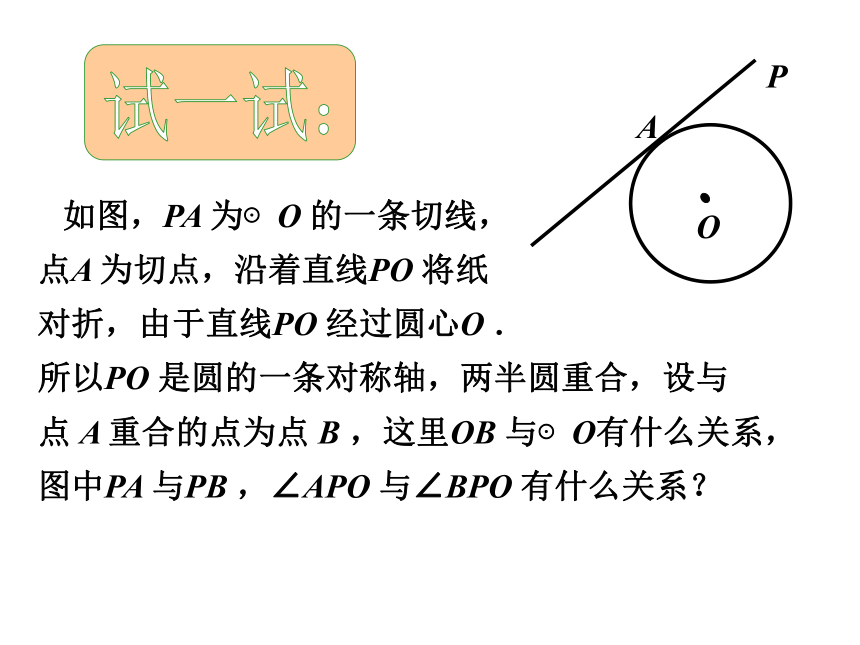
课件15张PPT。O。P 1.任意画一个⊙O ,在⊙O上任取两点A,B,以A,B为切点分别作⊙O的两条切线,画出的两条切线的位置关系怎样?2.圆的切线是线段、射线、还是直线? 如图,PA 为⊙O 的一条切线,
点A 为切点,沿着直线PO 将纸
对折,由于直线PO 经过圆心O .
所以PO 是圆的一条对称轴,两半圆重合,设与
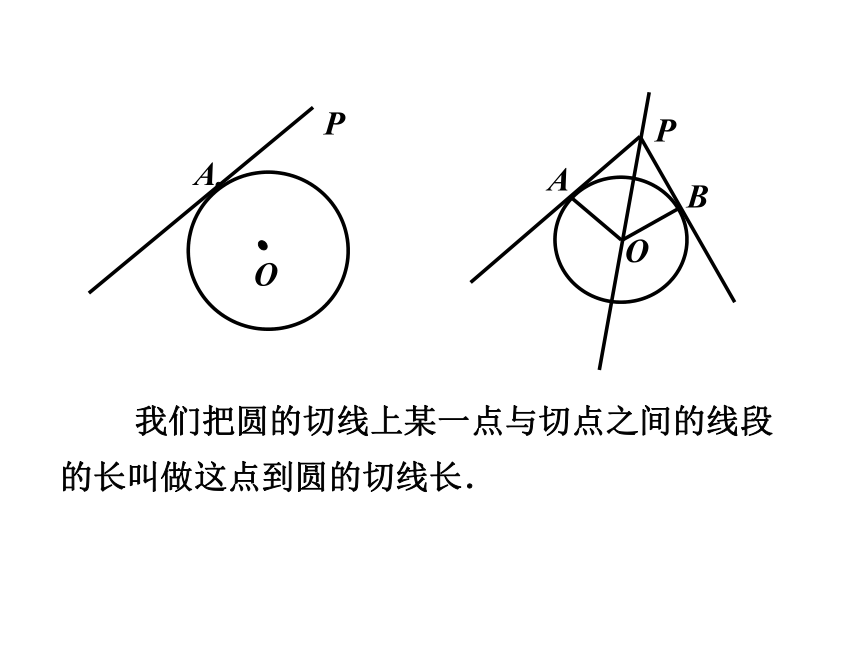
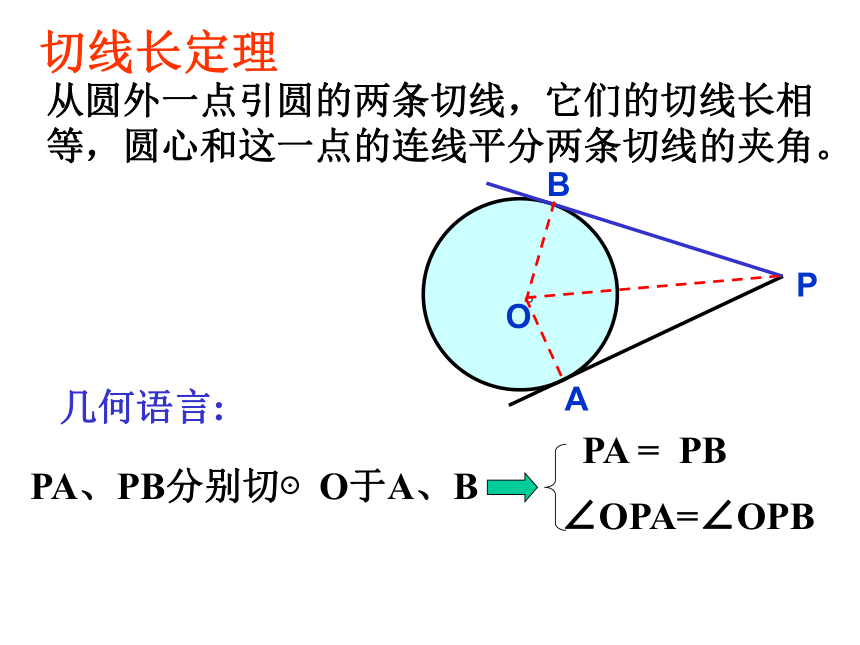
点 A 重合的点为点 B ,这里OB 与⊙O有什么关系,图中PA 与PB ,∠APO 与∠BPO 有什么关系? OAP 我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长. 切线与切线长的区别与联系: (1)切线是一条与圆相切的直线;切线长是一条线段.(2)切线长是指切线上某一点与切点间的线段的长。PA、PB分别切⊙O于A、BPA = PB∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 切线长定理几何语言:我们学过的切线,常有 五个 性质:
1、切线和圆只有一个公共点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线必过圆心。6、从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。六个 连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
即△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB例1 已知:如图,PA,PB是⊙O的两条切线,A、B为切点。直线OP交⊙O于点D、E,交AB于点C。(1)写出图中所有的垂直关系;(3)如果PA=4cm,PD=2cm,求半径OA的长。OA⊥PA,OB⊥PB,OP⊥AB(2)图中有哪些线段
相等、弧相等,角相等? 2. 如图,四边形ABCD的边 AB,BC,CD,DA和⊙O分别相切于L,M,N,P。
(1)图中有几对相等的线段?(2)由此你能发现什么结论? 为什么?∵ AB,BC,CD,DA都与⊙O相切,
L,M,N,P是切点,∴AL=AP,LB=MB,
DN=DP,NC=MC∴AL+ LB+ DN+ NC = AP+ MB+DP+MC即 AB+ CD = AD+BC圆的外切四边形的两组对边的和相等(可做定理用)1、填空:已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。60练 习:练 习:2、已知圆外切四边形ABCD中,AB:BC:CD=4:3:2,它的周长为24cm。则
AB= ,BC= ;
CD= ,DA= 。8cm6cm4cm6cm 3. 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
? 幻灯片 15解:设AF=Xcm,BD=Ycm,CE=Zcm则AE=AF=Xcm,DC=BD=Ycm,AE=EC=Zcm依题意得
方程组如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。4、直角三角形的两直角边分别是a,b 则其内切圆的半径为:2cm1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 小 结:∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPBOP垂直平分AB 切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了思考方向。这个图形包含着切线长定理,垂径定理,勾股定理,等腰三角形的三线合一以及两个直角三角形相似等知识必须掌握并能灵活应用。2.圆的外切四边形的两组对边的和相等
点A 为切点,沿着直线PO 将纸
对折,由于直线PO 经过圆心O .
所以PO 是圆的一条对称轴,两半圆重合,设与
点 A 重合的点为点 B ,这里OB 与⊙O有什么关系,图中PA 与PB ,∠APO 与∠BPO 有什么关系? OAP 我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长. 切线与切线长的区别与联系: (1)切线是一条与圆相切的直线;切线长是一条线段.(2)切线长是指切线上某一点与切点间的线段的长。PA、PB分别切⊙O于A、BPA = PB∠OPA=∠OPB
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 切线长定理几何语言:我们学过的切线,常有 五个 性质:
1、切线和圆只有一个公共点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线必过圆心。6、从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。六个 连结两切点A、B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
即△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB例1 已知:如图,PA,PB是⊙O的两条切线,A、B为切点。直线OP交⊙O于点D、E,交AB于点C。(1)写出图中所有的垂直关系;(3)如果PA=4cm,PD=2cm,求半径OA的长。OA⊥PA,OB⊥PB,OP⊥AB(2)图中有哪些线段
相等、弧相等,角相等? 2. 如图,四边形ABCD的边 AB,BC,CD,DA和⊙O分别相切于L,M,N,P。
(1)图中有几对相等的线段?(2)由此你能发现什么结论? 为什么?∵ AB,BC,CD,DA都与⊙O相切,
L,M,N,P是切点,∴AL=AP,LB=MB,
DN=DP,NC=MC∴AL+ LB+ DN+ NC = AP+ MB+DP+MC即 AB+ CD = AD+BC圆的外切四边形的两组对边的和相等(可做定理用)1、填空:已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。60练 习:练 习:2、已知圆外切四边形ABCD中,AB:BC:CD=4:3:2,它的周长为24cm。则
AB= ,BC= ;
CD= ,DA= 。8cm6cm4cm6cm 3. 已知:△ABC是⊙O外切三角形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
? 幻灯片 15解:设AF=Xcm,BD=Ycm,CE=Zcm则AE=AF=Xcm,DC=BD=Ycm,AE=EC=Zcm依题意得
方程组如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。4、直角三角形的两直角边分别是a,b 则其内切圆的半径为:2cm1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 小 结:∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPBOP垂直平分AB 切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了思考方向。这个图形包含着切线长定理,垂径定理,勾股定理,等腰三角形的三线合一以及两个直角三角形相似等知识必须掌握并能灵活应用。2.圆的外切四边形的两组对边的和相等
