23.2.4 切线的性质与切线长定理[上学期]
文档属性
| 名称 | 23.2.4 切线的性质与切线长定理[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 355.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-05 00:00:00 | ||
图片预览



文档简介
课件20张PPT。问题:
⒈前面我们已学过的切线的性质有哪些?
答:①、切线和圆有且只有一个公共点;
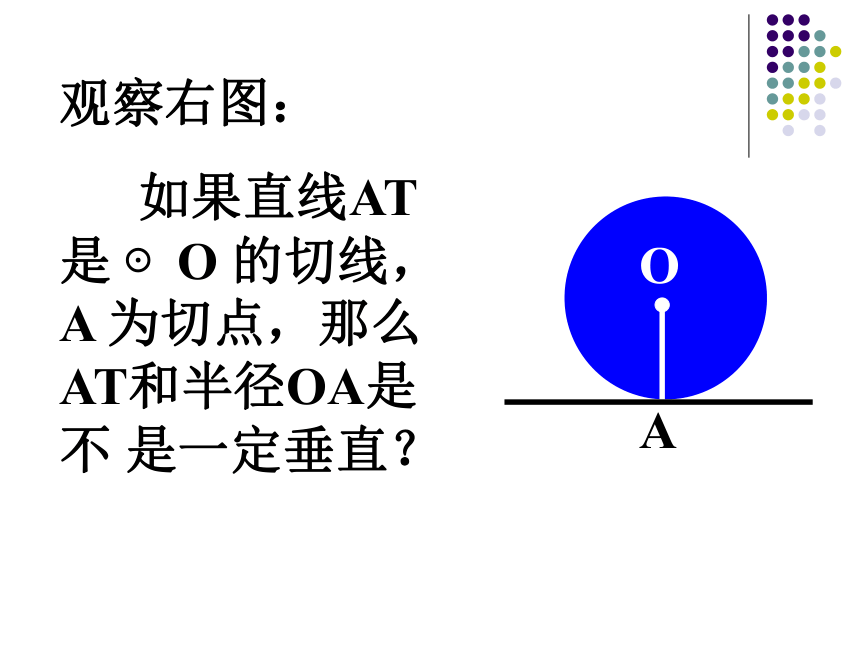
②、切线和圆心的距离等于半径。⒉切线还有什么性质?观察右图:
如果直线AT是 ⊙O 的切线,A 为切点,那么AT和半径OA是 不 是一定垂直?ATOM[切线的性质]
圆的切线垂直于经过切点的半径 推论1 经过圆心且垂直于切线的直线必经过切点推论2 经过切点且垂直于切线的直线必经过圆心123OBACD例 如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
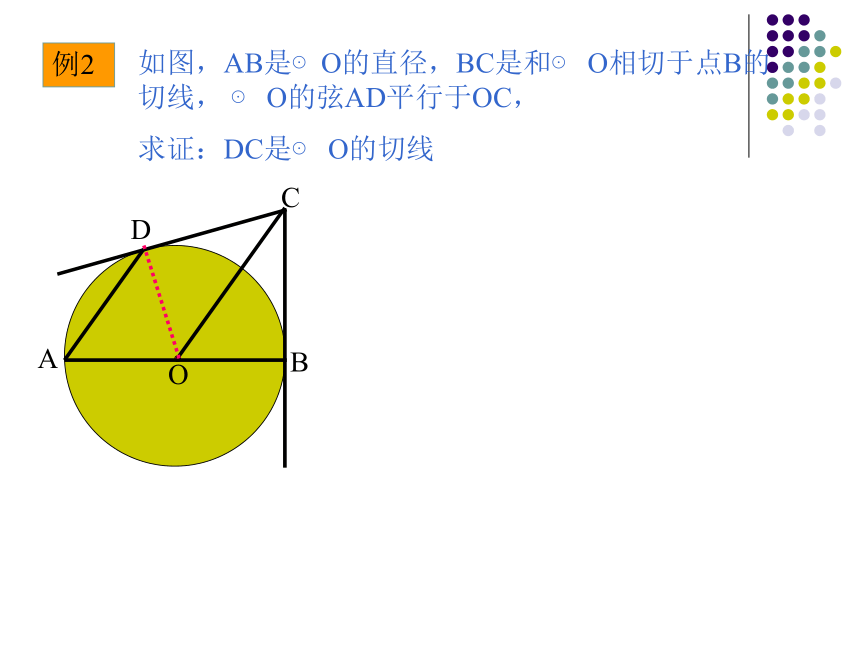
求证:AC平分∠DAB.例2如图,AB是⊙O的直径,BC是和⊙ O相切于点B的切线, ⊙ O的弦AD平行于OC,
求证:DC是⊙ O的切线COBDA练习1
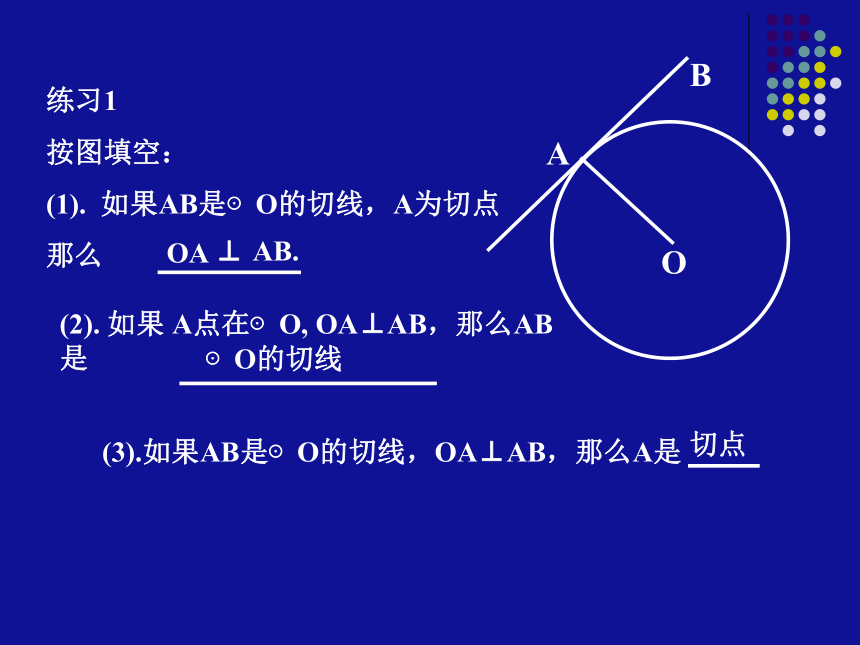
按图填空:
(1). 如果AB是⊙O的切线,A为切点
那么AOB⊙O的切线(2). 如果 A点在⊙O, OA⊥AB,那么AB是切点练习2
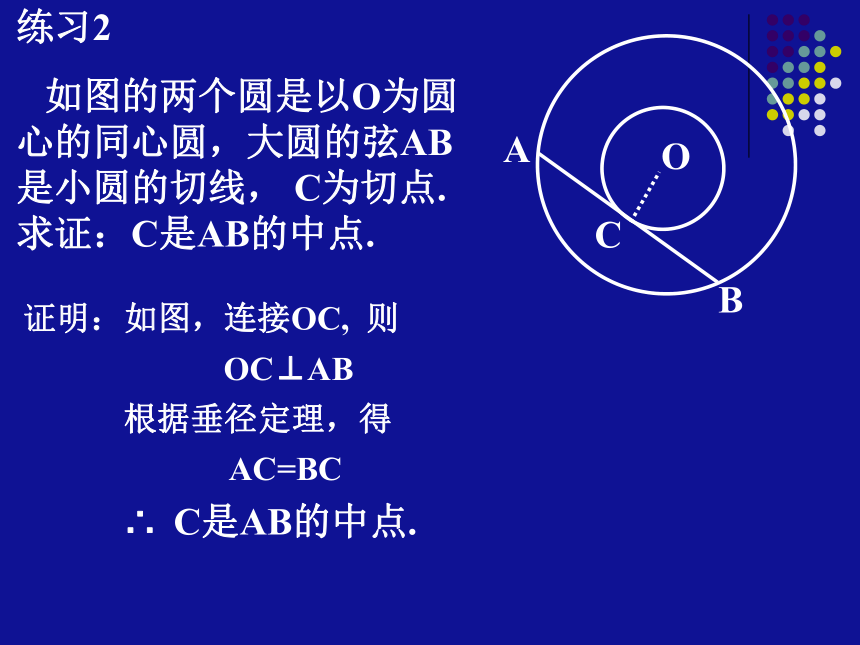
如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.CABO证明:如图,∴ C是AB的中点.AC=BC根据垂径定理,得OC⊥AB连接OC, 则DCBOA练习3
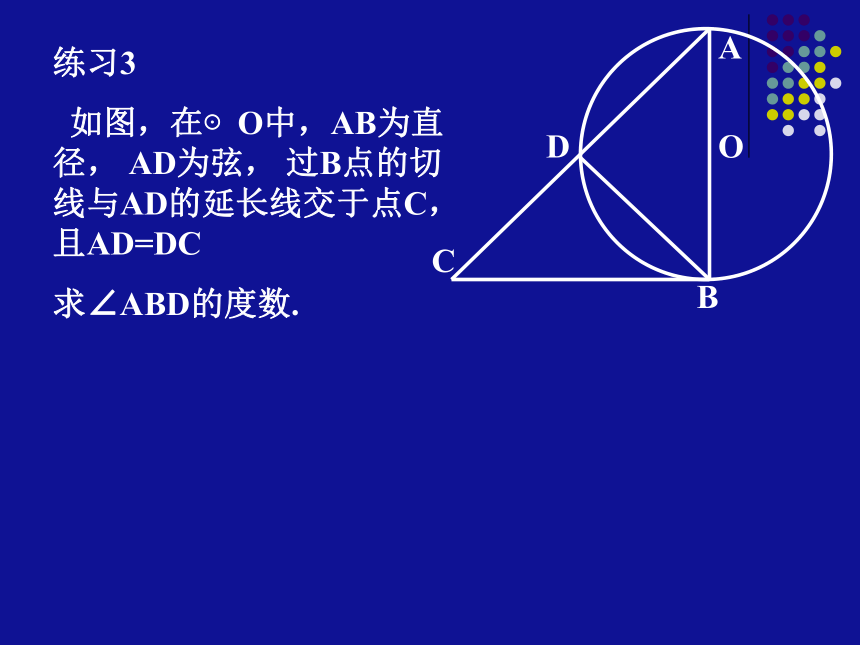
如图,在⊙O中,AB为直径, AD为弦, 过B点的切线与AD的延长线交于点C,且AD=DC
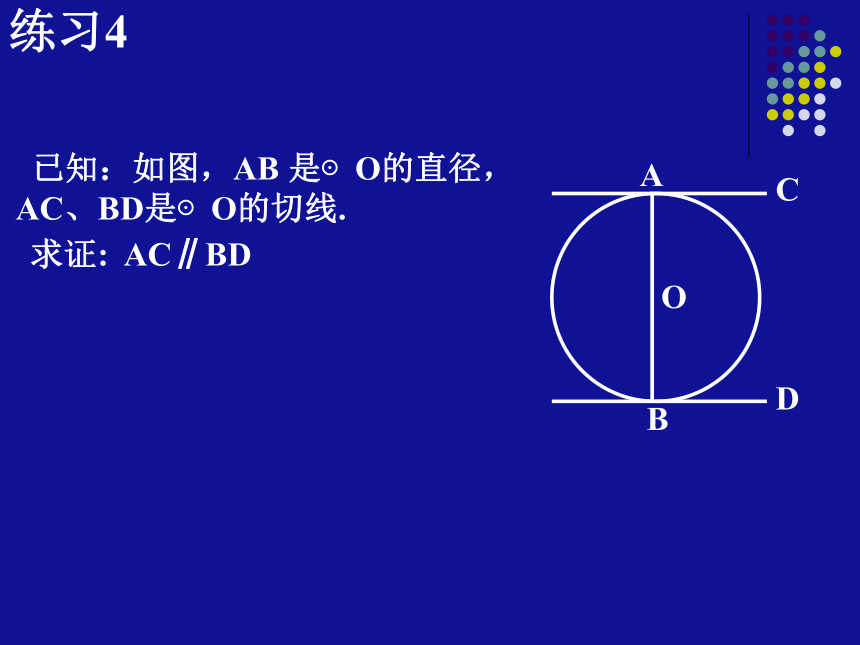
求∠ABD的度数.练习4 已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.
求证: AC∥BD 这是一位同学运动完后放的篮球,如果截它的平面,那么你能从中发现什么几何知识呢?墙 地面 P经过圆外一点可以有两条直线与圆相切二探索PBCO切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。思考:切线长和切线的区别和联系?小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。下面进一步探讨,先请一些同学做小实验:(2)请根据你的观察尝试总结它们之间的关系。(1)请同学们观察当圆变化时,切线长 PA、 PB之间的关系,同时观察
∠1,∠2的关系。pABO已知: 求证:如图,P为⊙ O外一点,PA、PB为⊙ O的切线,A、B为切点,连结PO你能不能用所
学的几何知识
证明刚才的实验?从你实验的观察和你的证明你能得出怎样的结论呢?切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。pABO请你们结合图形用数学语言表达定理∵PA、PB分别切⊙O于A、B,连结PO∴PA = PB,∠OPA=∠OPB
一判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。( )
练习二填空选择(1)如图:PA,PB切圆于A,B两点,
∠APB=50度,连结PO,
则∠APO=25°(2)如图,Δ ABC的内切圆分别和BC,AC,AB切于D,E,F;如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB= (3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )AP116cm9cmABD三、综合练习
已知:如图PA、PB是⊙ O的两条切线,A、B为切点。直线OP交⊙ O于D、E,交AB于C。(2)图中的直角三角形有 个,分别是36260Rt△OAP,Rt△OAP,Rt △ACORt△ACP,Rt △BCO, Rt △BCP△AOB, △APB(4)如果PA=4cm,PD=2cm,试求半径OA的长。x解:设OA= x cm,则PO= + = cm在RtΔ OAP中,PA= 4cm,由勾股定理得 即:解得: x=PDOD(x+2)3cm半径OA的长为3cm1、本节学习了切线长的定义,注意和切线比较。学习了切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。2、希望同学们在以后的学习中要勇于探索和实践,养成科学的学习态度。同时还要注意总结作辅助线的方法,和解题时要注意运用“数形结合”的思想方法。pO小结AB
⒈前面我们已学过的切线的性质有哪些?
答:①、切线和圆有且只有一个公共点;
②、切线和圆心的距离等于半径。⒉切线还有什么性质?观察右图:
如果直线AT是 ⊙O 的切线,A 为切点,那么AT和半径OA是 不 是一定垂直?ATOM[切线的性质]
圆的切线垂直于经过切点的半径 推论1 经过圆心且垂直于切线的直线必经过切点推论2 经过切点且垂直于切线的直线必经过圆心123OBACD例 如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.例2如图,AB是⊙O的直径,BC是和⊙ O相切于点B的切线, ⊙ O的弦AD平行于OC,
求证:DC是⊙ O的切线COBDA练习1
按图填空:
(1). 如果AB是⊙O的切线,A为切点
那么AOB⊙O的切线(2). 如果 A点在⊙O, OA⊥AB,那么AB是切点练习2
如图的两个圆是以O为圆心的同心圆,大圆的弦AB是小圆的切线, C为切点.求证:C是AB的中点.CABO证明:如图,∴ C是AB的中点.AC=BC根据垂径定理,得OC⊥AB连接OC, 则DCBOA练习3
如图,在⊙O中,AB为直径, AD为弦, 过B点的切线与AD的延长线交于点C,且AD=DC
求∠ABD的度数.练习4 已知:如图,AB 是⊙O的直径,AC、BD是⊙O的切线.
求证: AC∥BD 这是一位同学运动完后放的篮球,如果截它的平面,那么你能从中发现什么几何知识呢?墙 地面 P经过圆外一点可以有两条直线与圆相切二探索PBCO切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。思考:切线长和切线的区别和联系?小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。下面进一步探讨,先请一些同学做小实验:(2)请根据你的观察尝试总结它们之间的关系。(1)请同学们观察当圆变化时,切线长 PA、 PB之间的关系,同时观察
∠1,∠2的关系。pABO已知: 求证:如图,P为⊙ O外一点,PA、PB为⊙ O的切线,A、B为切点,连结PO你能不能用所
学的几何知识
证明刚才的实验?从你实验的观察和你的证明你能得出怎样的结论呢?切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。pABO请你们结合图形用数学语言表达定理∵PA、PB分别切⊙O于A、B,连结PO∴PA = PB,∠OPA=∠OPB
一判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。( )
练习二填空选择(1)如图:PA,PB切圆于A,B两点,
∠APB=50度,连结PO,
则∠APO=25°(2)如图,Δ ABC的内切圆分别和BC,AC,AB切于D,E,F;如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB= (3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )AP116cm9cmABD三、综合练习
已知:如图PA、PB是⊙ O的两条切线,A、B为切点。直线OP交⊙ O于D、E,交AB于C。(2)图中的直角三角形有 个,分别是36260Rt△OAP,Rt△OAP,Rt △ACORt△ACP,Rt △BCO, Rt △BCP△AOB, △APB(4)如果PA=4cm,PD=2cm,试求半径OA的长。x解:设OA= x cm,则PO= + = cm在RtΔ OAP中,PA= 4cm,由勾股定理得 即:解得: x=PDOD(x+2)3cm半径OA的长为3cm1、本节学习了切线长的定义,注意和切线比较。学习了切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。2、希望同学们在以后的学习中要勇于探索和实践,养成科学的学习态度。同时还要注意总结作辅助线的方法,和解题时要注意运用“数形结合”的思想方法。pO小结AB
