人教版数学八年级下册18.1.2平行四边形的判定 说课稿(共18张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.1.2平行四边形的判定 说课稿(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 14:22:48 | ||
图片预览


文档简介
(共18张PPT)
平行四边形的判定
目录
1
教学分析
2
教学目标
教学方法
教学过程
2
1
3
4
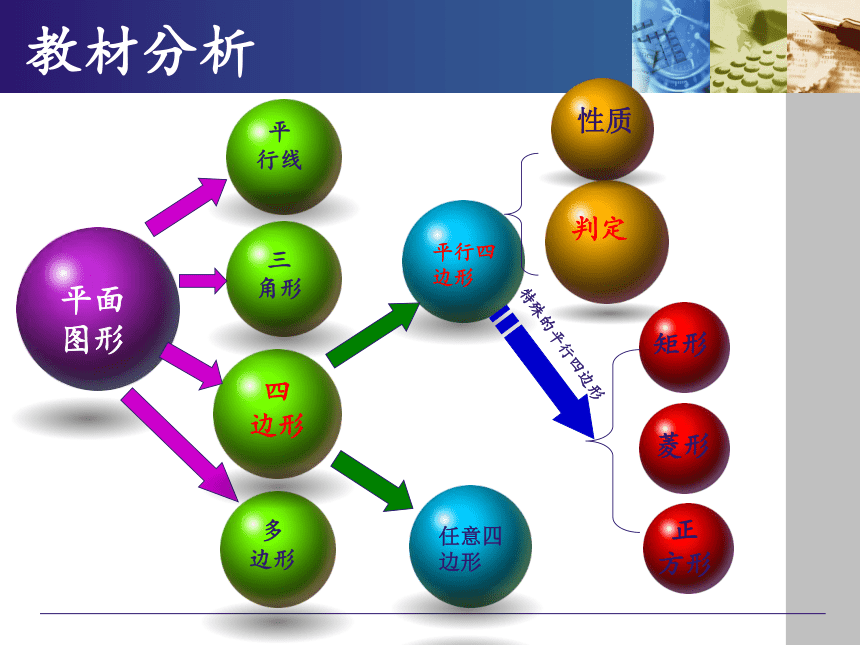
平面
图形
平行四边形
教材分析
三
角形
四
边形
多
边形
任意四边形
性质
判定
平
行线
矩形
菱形
正
方形
特殊的平行四边形
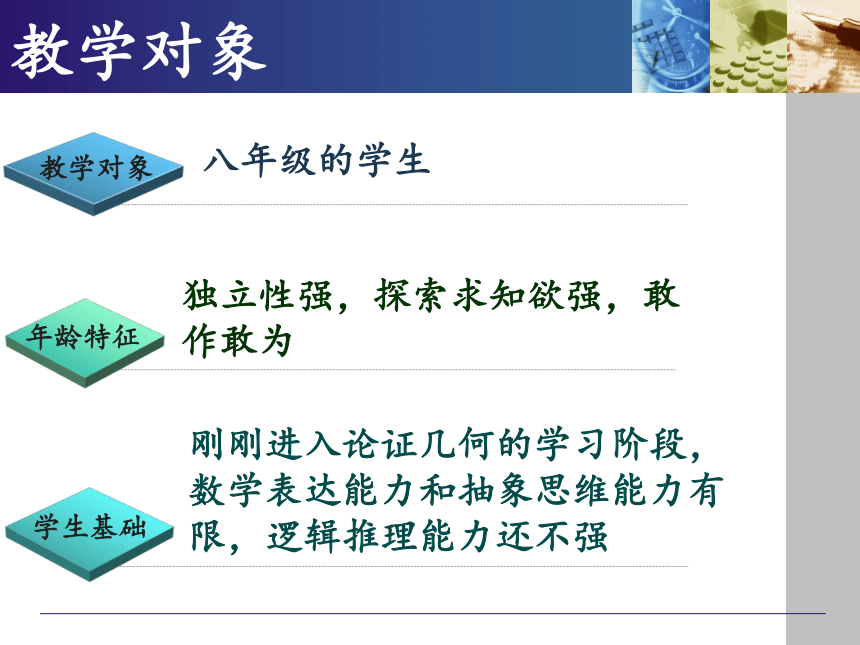
教学对象
年龄特征
学生基础
教学对象
八年级的学生
刚刚进入论证几何的学习阶段,数学表达能力和抽象思维能力有限,逻辑推理能力还不强
独立性强,探索求知欲强,敢作敢为
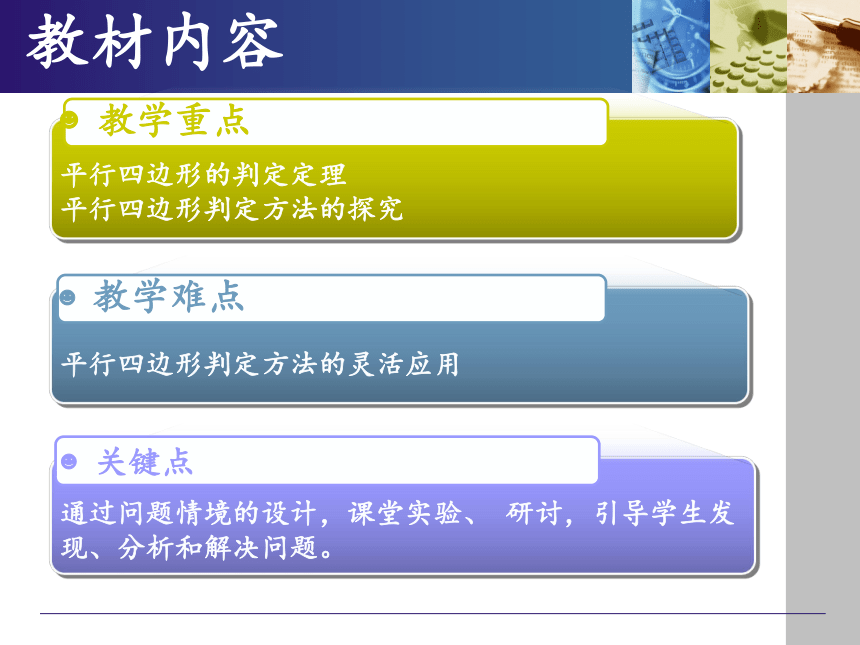
平行四边形的判定定理
平行四边形判定方法的探究
平行四边形判定方法的灵活应用
通过问题情境的设计,课堂实验、 研讨,引导学生发现、分析和解决问题。
教学重点
教学难点
关键点
教材内容
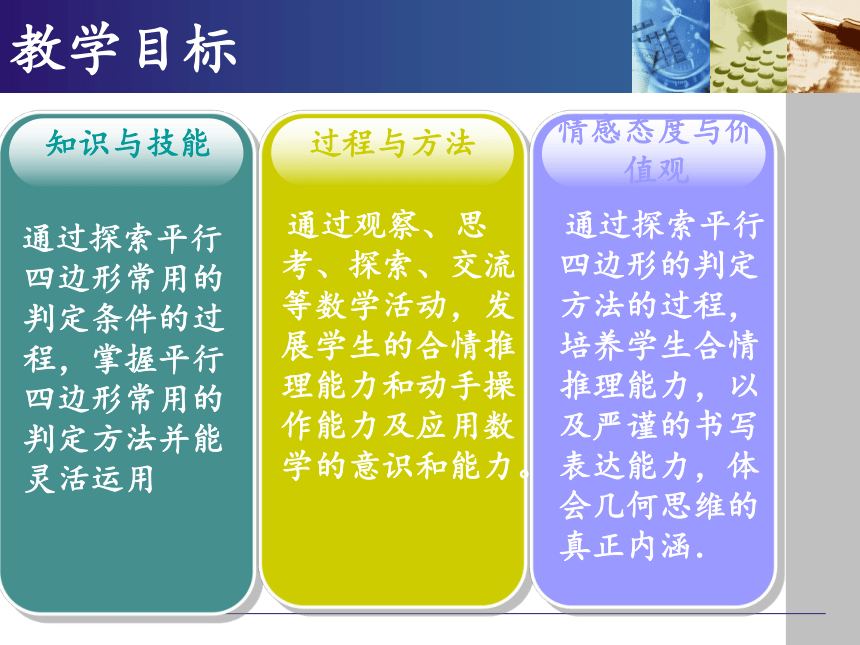
通过探索平行四边形常用的判定条件的过程,掌握平行四边形常用的判定方法并能灵活运用
通过观察、思考、探索、交流等数学活动,发展学生的合情推理能力和动手操作能力及应用数学的意识和能力。
通过探索平行四边形的判定方法的过程, 培养学生合情推理能力,以及严谨的书写表达能力,体会几何思维的真正内涵.
知识与技能
教学目标
过程与方法
情感态度与价值观
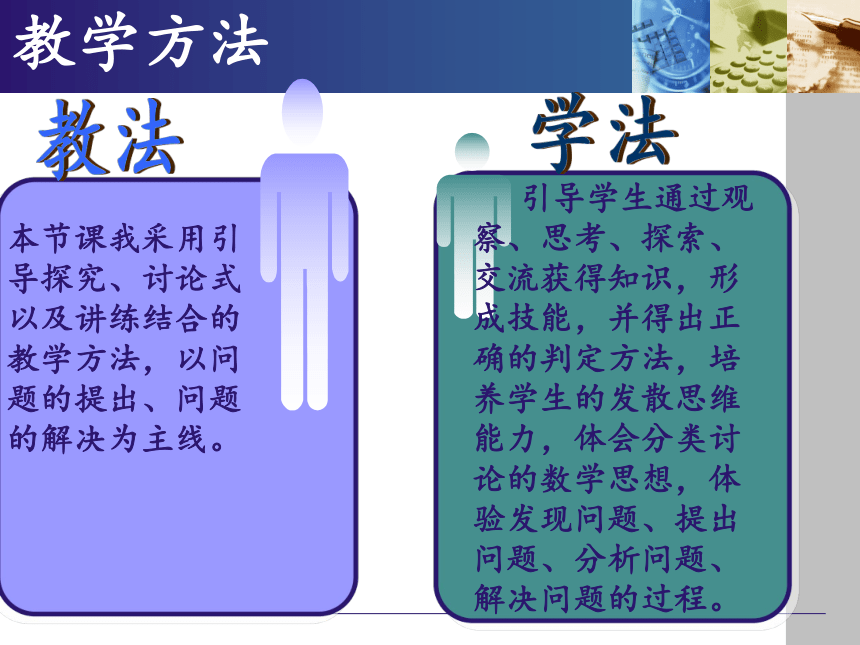
本节课我采用引
导探究、讨论式
以及讲练结合的
教学方法,以问
题的提出、问题
的解决为主线。
教学方法
引导学生通过观 察、思考、探索、交流获得知识,形成技能,并得出正确的判定方法,培养学生的发散思维能力,体会分类讨论的数学思想,体验发现问题、提出问题、分析问题、解决问题的过程。
Himart
教学手段
借助实物教具进行演示;采用多媒体辅助教学,以直观呈现教学素材,从而更好的激发学生的学习兴趣,增大教学容量,提高教学效率。
教学过程
约 5分钟
约 3分钟
提出问题
合作探究
约 3分钟
课堂练习
布置作业
教学流程
约 20分钟
复习引入
创设情境
总结归纳
例题讲解
约 12分钟
约 2分钟
判定的探究
判定的应用
教学过程
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
复行四边形的性质
(1) 平行四边形的对边
互相平行
(2)平行四边形的对边相等
(3)平行四边形的对角相等
(4)平行四边形的对角线
互相平分
教学过程
从学生已有的知识体系出发,平行四边形的性
质是本节课深入研究的认知基础,这样设计有利于引导学生顺利地进入学习情境。
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
从旧知识问题引入新课,提出具有启发性的问题,能够调动学生的积极思维,激起学生的学习欲望,也为下面探究平行四边形的判定方法打下基础。
提出问题?
(1)平行四边形的性质的逆命题成立吗?
(2怎样判断一个四边形是平行四边形?
教学过程
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
采取教师引导学生探究、讨论,让学生经历发现,说明,完善的过程,培养其操作说理、观察归纳的能力。从而可以帮助学生形成分析、对比、归纳的思想方法。
教学过程
Add Your Title
1
探究一:将两长两短的四根细木条用小钉绞合在一起,作成一个四边形,使等长的木条成为对边。转动这个四边形,使它改变形状,在图形变化的过程中,它一直是一个平行四边形吗?请说出其中的道理
2
探究二:在钉制平行四边形框架时采用了下面的方法。
将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形。请你说出其中的道理
B
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
总结规律:
1、两组对边分别相
等的四边形是平行四
边形;
2、两条对角线互相
平分的四边形是平行
四边形。
教学过程
教学过程
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
例3,演练题
例3、 平行四边形ABCD的对角线AC,BD交于点O,E、F是AC上的两点,并且AE=CF.求证四边形BFDE是平行四边形
演练题:在平行四边形ABCD中,E、F分别是AB、CD的中点,四边形AECF是平行四边形吗?证明你的结论.
(例1)
1、如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?
练习1、2
A
D
B
F
E
2、求证:两组对角分别相等的四边形是平行四边形
C
教学评价
本节课教学过程中通过问题设置,引发学生学习的兴趣,引导学生主动探索,通过对平行四边形判别方法的讨论发现新知,归纳总结,得出结论。本节内容逻辑性较强,对学生的逻辑思维能力要求较高,学生在说理上存在一定困难是正常的。但在问题讨论、引导发现、巩固训练的过程中,师生的信息交流畅通,反馈评价及时,学生与学生积极交流、讨论、思维活跃,教学活动始终处于教师的期盼控制中。
评价分析
板书设计
平行四边形的判定
平行四边形的判定定理 定理1:两组对边分别相 等的四边形是平行 四边形 定理2:对角线互相平分 的四边形是平行 四边形
例1的证明: 四边形ABCD是平行四边形 有AO=CO,BO=DO AE=CF 则EO=FO 又BO=DO 所以四边形BFDE是平行四边形
演练题的证明 四边形ABCD是平行四边形 有:AB=CD E,F分别是AB,CD的中点 可得BE=DF 又BC=AB ∠B=∠D 所以△BCE与△DAF 因此 AF=EC 又因为DF=BE 所以四边形AECF是平行四边形(定理1)
平行四边形的判定
目录
1
教学分析
2
教学目标
教学方法
教学过程
2
1
3
4
平面
图形
平行四边形
教材分析
三
角形
四
边形
多
边形
任意四边形
性质
判定
平
行线
矩形
菱形
正
方形
特殊的平行四边形
教学对象
年龄特征
学生基础
教学对象
八年级的学生
刚刚进入论证几何的学习阶段,数学表达能力和抽象思维能力有限,逻辑推理能力还不强
独立性强,探索求知欲强,敢作敢为
平行四边形的判定定理
平行四边形判定方法的探究
平行四边形判定方法的灵活应用
通过问题情境的设计,课堂实验、 研讨,引导学生发现、分析和解决问题。
教学重点
教学难点
关键点
教材内容
通过探索平行四边形常用的判定条件的过程,掌握平行四边形常用的判定方法并能灵活运用
通过观察、思考、探索、交流等数学活动,发展学生的合情推理能力和动手操作能力及应用数学的意识和能力。
通过探索平行四边形的判定方法的过程, 培养学生合情推理能力,以及严谨的书写表达能力,体会几何思维的真正内涵.
知识与技能
教学目标
过程与方法
情感态度与价值观
本节课我采用引
导探究、讨论式
以及讲练结合的
教学方法,以问
题的提出、问题
的解决为主线。
教学方法
引导学生通过观 察、思考、探索、交流获得知识,形成技能,并得出正确的判定方法,培养学生的发散思维能力,体会分类讨论的数学思想,体验发现问题、提出问题、分析问题、解决问题的过程。
Himart
教学手段
借助实物教具进行演示;采用多媒体辅助教学,以直观呈现教学素材,从而更好的激发学生的学习兴趣,增大教学容量,提高教学效率。
教学过程
约 5分钟
约 3分钟
提出问题
合作探究
约 3分钟
课堂练习
布置作业
教学流程
约 20分钟
复习引入
创设情境
总结归纳
例题讲解
约 12分钟
约 2分钟
判定的探究
判定的应用
教学过程
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
复行四边形的性质
(1) 平行四边形的对边
互相平行
(2)平行四边形的对边相等
(3)平行四边形的对角相等
(4)平行四边形的对角线
互相平分
教学过程
从学生已有的知识体系出发,平行四边形的性
质是本节课深入研究的认知基础,这样设计有利于引导学生顺利地进入学习情境。
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
从旧知识问题引入新课,提出具有启发性的问题,能够调动学生的积极思维,激起学生的学习欲望,也为下面探究平行四边形的判定方法打下基础。
提出问题?
(1)平行四边形的性质的逆命题成立吗?
(2怎样判断一个四边形是平行四边形?
教学过程
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
采取教师引导学生探究、讨论,让学生经历发现,说明,完善的过程,培养其操作说理、观察归纳的能力。从而可以帮助学生形成分析、对比、归纳的思想方法。
教学过程
Add Your Title
1
探究一:将两长两短的四根细木条用小钉绞合在一起,作成一个四边形,使等长的木条成为对边。转动这个四边形,使它改变形状,在图形变化的过程中,它一直是一个平行四边形吗?请说出其中的道理
2
探究二:在钉制平行四边形框架时采用了下面的方法。
将两根木条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形。请你说出其中的道理
B
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
布置作业
总结规律:
1、两组对边分别相
等的四边形是平行四
边形;
2、两条对角线互相
平分的四边形是平行
四边形。
教学过程
教学过程
判定的探究
判定的应用
复习引入
提出问题
合作探究
归纳总结
例题讲解
课堂练习
例3,演练题
例3、 平行四边形ABCD的对角线AC,BD交于点O,E、F是AC上的两点,并且AE=CF.求证四边形BFDE是平行四边形
演练题:在平行四边形ABCD中,E、F分别是AB、CD的中点,四边形AECF是平行四边形吗?证明你的结论.
(例1)
1、如图,AB=DC=EF,AD=BC,DE=CF,图中有哪些互相平行的线段?
练习1、2
A
D
B
F
E
2、求证:两组对角分别相等的四边形是平行四边形
C
教学评价
本节课教学过程中通过问题设置,引发学生学习的兴趣,引导学生主动探索,通过对平行四边形判别方法的讨论发现新知,归纳总结,得出结论。本节内容逻辑性较强,对学生的逻辑思维能力要求较高,学生在说理上存在一定困难是正常的。但在问题讨论、引导发现、巩固训练的过程中,师生的信息交流畅通,反馈评价及时,学生与学生积极交流、讨论、思维活跃,教学活动始终处于教师的期盼控制中。
评价分析
板书设计
平行四边形的判定
平行四边形的判定定理 定理1:两组对边分别相 等的四边形是平行 四边形 定理2:对角线互相平分 的四边形是平行 四边形
例1的证明: 四边形ABCD是平行四边形 有AO=CO,BO=DO AE=CF 则EO=FO 又BO=DO 所以四边形BFDE是平行四边形
演练题的证明 四边形ABCD是平行四边形 有:AB=CD E,F分别是AB,CD的中点 可得BE=DF 又BC=AB ∠B=∠D 所以△BCE与△DAF 因此 AF=EC 又因为DF=BE 所以四边形AECF是平行四边形(定理1)
