甘肃省临夏州临夏县2022-2023学年高二下学期期中考试数学试题(Word版含答案)
文档属性
| 名称 | 甘肃省临夏州临夏县2022-2023学年高二下学期期中考试数学试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 556.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 00:00:00 | ||
图片预览

文档简介
临夏县2022-2023学年高二下学期期中考试
数学
一、单选题(共40分)
1.已知某生产厂家的年利润y与年投入广告费x满足的函数关系式为,则当x由1增长到3时,y的平均变化率为( )
A.2 B.3 C.4 D.6
2.设存在导数,且满足,则曲线在处的切线倾斜角为( )
A.30° B.135° C.45° D.120°
3.函数的图像如图所示,则关于函数的说法正确的是( )
A.函数有3个极值点
B.函数在区间上是增加的
C.函数在区间上是增加的
D.当时,函数取得极大值
4.已知是函数的导函数,若,则( )
A. B. C. D.
5.已知没有极值,则实数的取值范围是( )
A. B. C. D.
6.空间两点A,B的坐标分别为,则A,B两点的位置关系是( )
A.关于x轴对称 B.关于平面对称 C.关于z轴对称 D.关于原点对称
7.已知在平行六面体中,,且,则( )
A. B. C. D.
8.某公司生产一种产品,固定成本为元,每生产一单位的产品,成本增加元,若总收入与年产量的关系是,,则当总利润最大时,每年生产的产品单位数是( )
A. B. C. D.
二、多选题(共20分)
9.下列求导正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
10.已知函数,下列说法中正确的有( )
A.函数的极大值为,极小值为
B.当时,函数的最大值为,最小值为
C.函数的单调增区间为
D.曲线在点处的切线方程为
11.如图,E,F分别是长方体ABCD-A′B′C′D′的棱AB,CD的中点,化简下列结果正确的是( )
A. B.
C. D.
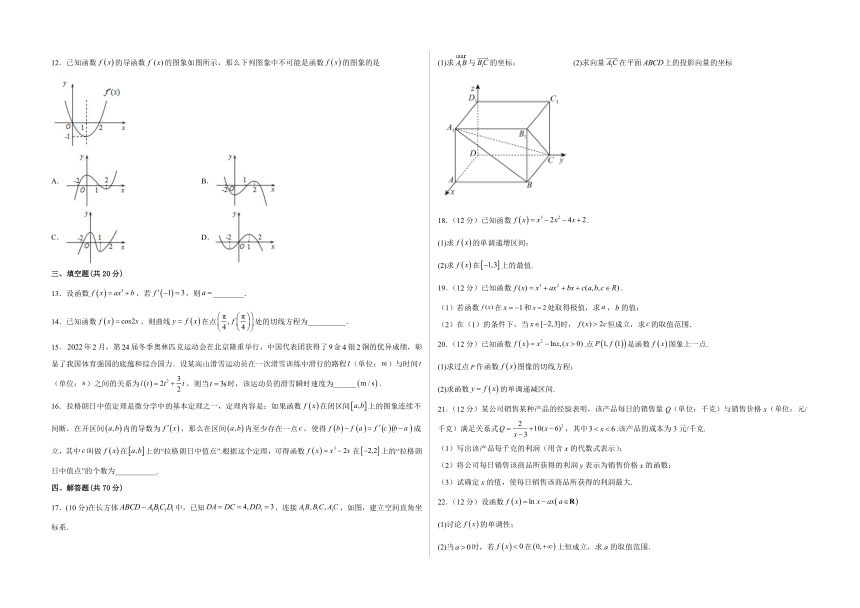
12.已知函数的导函数的图象如图所示,那么下列图象中不可能是函数的图象的是
A. B.
C. D.
三、填空题(共20分)
13.设函数,若,则________.
14.已知函数,则曲线在点处的切线方程为__________.
15.年月,第届冬季奥林匹克运动会在北京隆重举行,中国代表团获得了金银铜的优异成绩,彰显了我国体育强国的底蕴和综合国力.设某高山滑雪运动员在一次滑雪训练中滑行的路程(单位:)与时间(单位:)之间的关系为,则当时,该运动员的滑雪瞬时速度为______.
16.拉格朗日中值定理是微分学中的基本定理之一,定理内容是:如果函数在闭区间上的图象连续不间断,在开区间内的导数为,那么在区间内至少存在一点,使得成立,其中叫做在上的“拉格朗日中值点”.根据这个定理,可得函数在上的“拉格朗日中值点”的个数为___________.
四、解答题(共70分)
17.(10分)在长方体中,已知,连接,如图,建立空间直角坐标系.
(1)求与的坐标; (2)求向量在平面上的投影向量的坐标
18.(12分)已知函数.
(1)求的单调递增区间;
(2)求在上的最值.
19.(12分)已知函数.
(1)若函数在和处取得极值,求,的值;
(2)在(1)的条件下,当时,恒成立,求的取值范围.
20.(12分)已知函数.点是函数图象上一点.
(1)求过点作函数图像的切线方程;
(2)求函数的单调递减区间.
21.(12分)某公司销售某种产品的经验表明,该产品每日的销售量Q(单位:千克)与销售价格x(单位:元/千克)满足关系式,其中.该产品的成本为3元/千克.
(1)写出该产品每千克的利润(用含x的代数式表示);
(2)将公司每日销售该商品所获得的利润y表示为销售价格x的函数;
(3)试确定x的值,使每日销售该商品所获得的利润最大.
22.(12分)设函数
(1)讨论的单调性;
(2)当时,若在上恒成立,求a的取值范围.
高二数学期中考试答案
一、选择题
1.B 2.B 3.C 4.B 5.C 6.C 7.A 8.D
9.AD 10.AD 11.AB 12.BCD
二、填空题
13.1 14.
15. 16.
三、解答题
17.(1);;
(2).
【详解】(1)在长方体中,已知,
依题意,,
所以,.
(2)在长方体中,平面,连接AC,因此线段是线段在平面上射影,如图,
即向量在平面上的投影向量为,而,,
所以向量在平面上的投影向量的坐标为.
18.(1)的单调递增区间为,;
(2).
【详解】(1)因为.
所以,
由,可得或,
,的变化情况如下:
2
+ 0 0 +
递增 递减 递增
所以函数的单调递增区间为,;
(2)由(1)知,在上单调递增,在上单调递减,在上单调递增.
所以为极大值点,为极小值点,又,,,,
所以在上的值域为.
19.(1);(2).
【详解】(1)由题可得,,
∵函数在和处取得极值,
∴,2是方程的两根,
∴,∴;
(2)由(1)知,,
当变化时,,随的变化如下表:
2 3
0 0
增 减 增
∴当时,的最小值为,要使恒成立,只要即可,
∴,∴的取值范围为.
20.(1) (2)
【详解】(1)解:因为,所以,,
所以,即切点为,切线的斜率,
所以切线方程为,即;
(2)解:定义域为,且,
令,解得,
所以的单调递减区间为.
21.(1);(2),().
(3)销售价格为元时,每日销售该商品所获得的利润最大,最大值为元.
(1)
,().
(2)由(1)可得,
令,解得或,
令,解得或,
令,解得,
所以函数在上单调递增;在上单调递减,
所以当,(元)
故销售价格为元时,每日销售该商品所获得的利润最大,最大值为元.
22.(1)分类讨论,答案见解析.
(2)
【详解】(1)已知,则函数的定义域为,且,
当时,,在单调递增;
当,且时,,此时在上是增函数;
时,,此时在上是减函数.
综上所述,当时,在定义域上单调递增;
当时,在上单调递增,在上单调递减.
(2)当时,在上恒成立,
即在上恒成立,
设,则,
当时,,为增函数;
当时,,为减函数.
,则,
a的取值范围为.
数学
一、单选题(共40分)
1.已知某生产厂家的年利润y与年投入广告费x满足的函数关系式为,则当x由1增长到3时,y的平均变化率为( )
A.2 B.3 C.4 D.6
2.设存在导数,且满足,则曲线在处的切线倾斜角为( )
A.30° B.135° C.45° D.120°
3.函数的图像如图所示,则关于函数的说法正确的是( )
A.函数有3个极值点
B.函数在区间上是增加的
C.函数在区间上是增加的
D.当时,函数取得极大值
4.已知是函数的导函数,若,则( )
A. B. C. D.
5.已知没有极值,则实数的取值范围是( )
A. B. C. D.
6.空间两点A,B的坐标分别为,则A,B两点的位置关系是( )
A.关于x轴对称 B.关于平面对称 C.关于z轴对称 D.关于原点对称
7.已知在平行六面体中,,且,则( )
A. B. C. D.
8.某公司生产一种产品,固定成本为元,每生产一单位的产品,成本增加元,若总收入与年产量的关系是,,则当总利润最大时,每年生产的产品单位数是( )
A. B. C. D.
二、多选题(共20分)
9.下列求导正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
10.已知函数,下列说法中正确的有( )
A.函数的极大值为,极小值为
B.当时,函数的最大值为,最小值为
C.函数的单调增区间为
D.曲线在点处的切线方程为
11.如图,E,F分别是长方体ABCD-A′B′C′D′的棱AB,CD的中点,化简下列结果正确的是( )
A. B.
C. D.
12.已知函数的导函数的图象如图所示,那么下列图象中不可能是函数的图象的是
A. B.
C. D.
三、填空题(共20分)
13.设函数,若,则________.
14.已知函数,则曲线在点处的切线方程为__________.
15.年月,第届冬季奥林匹克运动会在北京隆重举行,中国代表团获得了金银铜的优异成绩,彰显了我国体育强国的底蕴和综合国力.设某高山滑雪运动员在一次滑雪训练中滑行的路程(单位:)与时间(单位:)之间的关系为,则当时,该运动员的滑雪瞬时速度为______.
16.拉格朗日中值定理是微分学中的基本定理之一,定理内容是:如果函数在闭区间上的图象连续不间断,在开区间内的导数为,那么在区间内至少存在一点,使得成立,其中叫做在上的“拉格朗日中值点”.根据这个定理,可得函数在上的“拉格朗日中值点”的个数为___________.
四、解答题(共70分)
17.(10分)在长方体中,已知,连接,如图,建立空间直角坐标系.
(1)求与的坐标; (2)求向量在平面上的投影向量的坐标
18.(12分)已知函数.
(1)求的单调递增区间;
(2)求在上的最值.
19.(12分)已知函数.
(1)若函数在和处取得极值,求,的值;
(2)在(1)的条件下,当时,恒成立,求的取值范围.
20.(12分)已知函数.点是函数图象上一点.
(1)求过点作函数图像的切线方程;
(2)求函数的单调递减区间.
21.(12分)某公司销售某种产品的经验表明,该产品每日的销售量Q(单位:千克)与销售价格x(单位:元/千克)满足关系式,其中.该产品的成本为3元/千克.
(1)写出该产品每千克的利润(用含x的代数式表示);
(2)将公司每日销售该商品所获得的利润y表示为销售价格x的函数;
(3)试确定x的值,使每日销售该商品所获得的利润最大.
22.(12分)设函数
(1)讨论的单调性;
(2)当时,若在上恒成立,求a的取值范围.
高二数学期中考试答案
一、选择题
1.B 2.B 3.C 4.B 5.C 6.C 7.A 8.D
9.AD 10.AD 11.AB 12.BCD
二、填空题
13.1 14.
15. 16.
三、解答题
17.(1);;
(2).
【详解】(1)在长方体中,已知,
依题意,,
所以,.
(2)在长方体中,平面,连接AC,因此线段是线段在平面上射影,如图,
即向量在平面上的投影向量为,而,,
所以向量在平面上的投影向量的坐标为.
18.(1)的单调递增区间为,;
(2).
【详解】(1)因为.
所以,
由,可得或,
,的变化情况如下:
2
+ 0 0 +
递增 递减 递增
所以函数的单调递增区间为,;
(2)由(1)知,在上单调递增,在上单调递减,在上单调递增.
所以为极大值点,为极小值点,又,,,,
所以在上的值域为.
19.(1);(2).
【详解】(1)由题可得,,
∵函数在和处取得极值,
∴,2是方程的两根,
∴,∴;
(2)由(1)知,,
当变化时,,随的变化如下表:
2 3
0 0
增 减 增
∴当时,的最小值为,要使恒成立,只要即可,
∴,∴的取值范围为.
20.(1) (2)
【详解】(1)解:因为,所以,,
所以,即切点为,切线的斜率,
所以切线方程为,即;
(2)解:定义域为,且,
令,解得,
所以的单调递减区间为.
21.(1);(2),().
(3)销售价格为元时,每日销售该商品所获得的利润最大,最大值为元.
(1)
,().
(2)由(1)可得,
令,解得或,
令,解得或,
令,解得,
所以函数在上单调递增;在上单调递减,
所以当,(元)
故销售价格为元时,每日销售该商品所获得的利润最大,最大值为元.
22.(1)分类讨论,答案见解析.
(2)
【详解】(1)已知,则函数的定义域为,且,
当时,,在单调递增;
当,且时,,此时在上是增函数;
时,,此时在上是减函数.
综上所述,当时,在定义域上单调递增;
当时,在上单调递增,在上单调递减.
(2)当时,在上恒成立,
即在上恒成立,
设,则,
当时,,为增函数;
当时,,为减函数.
,则,
a的取值范围为.
同课章节目录
