平均变化率(江苏省泰州市泰兴市)
图片预览





文档简介
课件17张PPT。平均变化率江苏省黄桥中学分校:殷峰一、问题情境平均速度的数学意义是什么 ? 法国《队报》网站的文章称刘翔以不可思议的速度统治了赛场。这名21岁的中国人跑的几乎比炮弹还快,赛道上显示的12.94秒的成绩已经打破了12.95奥运会记录,但经过验证他是以12.91秒平了世界纪录,他的平均速度达到8.52m/s。
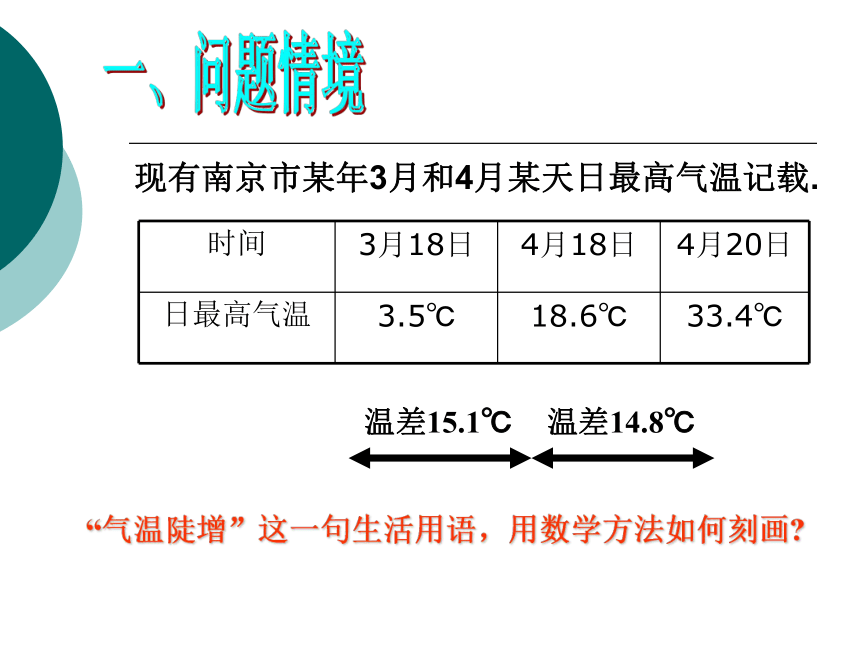
现有南京市某年3月和4月某天日最高气温记载.一、问题情境“气温陡增”这一句生活用语,用数学方法如何刻画? 温差15.1℃温差14.8℃一、问题情境联想
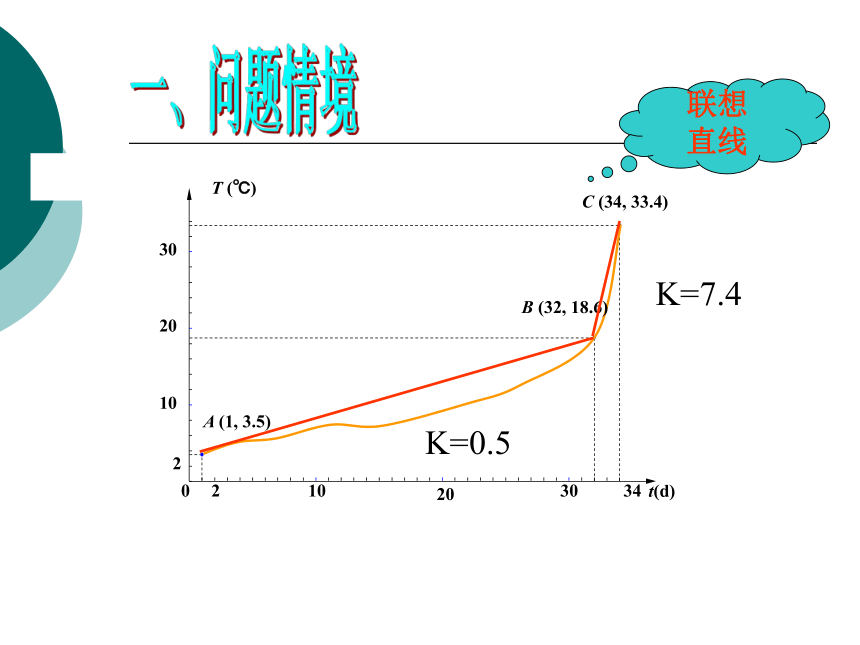
直线K=7.4K=0.5二、建构数学1、平均变化率 一般的,函数 在区间上 的
平均变化率为 2、平均变化率是曲线陡峭程度的“数量化”,
曲线陡峭程度是平均变化率“视觉化”.例1、 在经营某商品中,甲挣到10万元,乙挣到2万
元,如何比较和评价甲,乙两人的经营成果?三、数学运用 在经营某商品中,甲用5年时间挣到10万元,
乙用5个月时间挣到2万元,如何比较和评价甲,
乙两人的经营成果?1、某婴儿从出生到第12个月的体重变化如图所示,
试分别计算从出生到第3个月与第6个月到第12个
月该婴儿体重的平均变化率。四、课堂练习三、数学运用例2、水经过虹吸管从容器甲中流向容器乙,t s后
容器甲中水的体积 (单位: ),
计算第一个10s内V的平均变化率。例3、很多人都吹过气球,回忆一下吹气球的过程,随
着气球内空气容量的增加,气球的半径有如何变化?
从数学角度如何解释这种现象?三、数学运用计算气球的半径在 上的平均变化率 三、数学运用例4、已知函数 分
别计算在区间[-3,-1],[0,5]上 及
的平均变化率。 2、已知函数 ,分别计算 在
下列区间上的平均变化率: (1)[-1,2];
(2)[-1,1];
(3)[-1,-0.9]; 四、课堂练习三、数学运用例5、已知函数 ,分别计算 在下
列区间上的平均变化率: (1)[1,3];
(2)[1,2];
(3)[1,1.1];
(4)[1,1.001]。 432.12.001133、已知函数 ,分别计算 在下
列区间上的平均变化率: (1)[0.9,1];
(2)[0.99,1];
(3)[0.999,1].四、课堂练习1.991.91.999五、回顾反思1、平均变化率 一般的,函数 在区间上 的
平均变化率为 2、平均变化率是曲线陡峭程度的“数量化”,
是一种粗略的刻画--------导数再见
现有南京市某年3月和4月某天日最高气温记载.一、问题情境“气温陡增”这一句生活用语,用数学方法如何刻画? 温差15.1℃温差14.8℃一、问题情境联想
直线K=7.4K=0.5二、建构数学1、平均变化率 一般的,函数 在区间上 的
平均变化率为 2、平均变化率是曲线陡峭程度的“数量化”,
曲线陡峭程度是平均变化率“视觉化”.例1、 在经营某商品中,甲挣到10万元,乙挣到2万
元,如何比较和评价甲,乙两人的经营成果?三、数学运用 在经营某商品中,甲用5年时间挣到10万元,
乙用5个月时间挣到2万元,如何比较和评价甲,
乙两人的经营成果?1、某婴儿从出生到第12个月的体重变化如图所示,
试分别计算从出生到第3个月与第6个月到第12个
月该婴儿体重的平均变化率。四、课堂练习三、数学运用例2、水经过虹吸管从容器甲中流向容器乙,t s后
容器甲中水的体积 (单位: ),
计算第一个10s内V的平均变化率。例3、很多人都吹过气球,回忆一下吹气球的过程,随
着气球内空气容量的增加,气球的半径有如何变化?
从数学角度如何解释这种现象?三、数学运用计算气球的半径在 上的平均变化率 三、数学运用例4、已知函数 分
别计算在区间[-3,-1],[0,5]上 及
的平均变化率。 2、已知函数 ,分别计算 在
下列区间上的平均变化率: (1)[-1,2];
(2)[-1,1];
(3)[-1,-0.9]; 四、课堂练习三、数学运用例5、已知函数 ,分别计算 在下
列区间上的平均变化率: (1)[1,3];
(2)[1,2];
(3)[1,1.1];
(4)[1,1.001]。 432.12.001133、已知函数 ,分别计算 在下
列区间上的平均变化率: (1)[0.9,1];
(2)[0.99,1];
(3)[0.999,1].四、课堂练习1.991.91.999五、回顾反思1、平均变化率 一般的,函数 在区间上 的
平均变化率为 2、平均变化率是曲线陡峭程度的“数量化”,
是一种粗略的刻画--------导数再见
