九年级第二学期圆填空题题训练(含解析)
文档属性
| 名称 | 九年级第二学期圆填空题题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 297.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 15:55:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
绝密★启用前
九年级下册检测
第5章圆
第I卷(选择题)
一、填空题(共150分)
1.(本题10分)一个扇形的半径为3cm,面积为,则此扇形的圆心角为 .
2.(本题10分)用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是_____.
3.(本题10分)如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若AOC=80°,则ADB的度数为( )
A.40° B.50° C.60° D.20°
4.(本题10分)直角三角形的两边长分别为16和12,则此三角形的外接圆半径是_______.
5.(本题10分)圆锥底面圆半径为5,母线长为6,则圆锥侧面积等于_____.
6.(本题10分)如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2=_____°.
7.(本题10分)如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为______.
8.(本题10分)如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是______(结果保留)
9.(本题10分)如图,在扇形中,,分别是半径上的点,以为邻边的的顶点在上,若,则阴影部分图形的面积是________(结果保留).
10.(本题10分)如图,在扇形AOB中,,半径OC交弦AB于点D,且.若,则阴影部分的面积为_____.
11.(本题10分)如图所示的扇形中,,C为上一点,,连接,过C作的垂线交于点D,则图中阴影部分的面积为_______.
12.(本题10分)如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 ▲ (结果保留π).
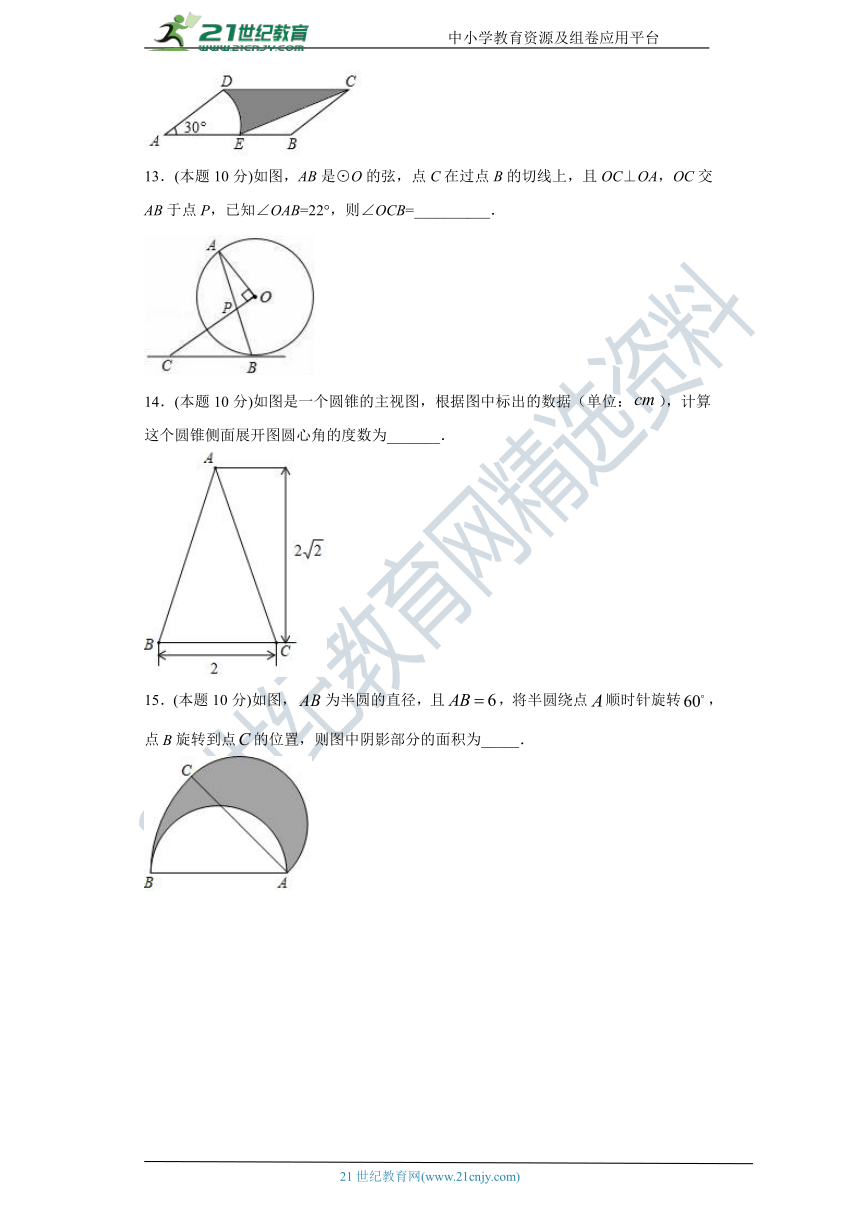
13.(本题10分)如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=__________.
14.(本题10分)如图是一个圆锥的主视图,根据图中标出的数据(单位:),计算这个圆锥侧面展开图圆心角的度数为_______.
15.(本题10分)如图,为半圆的直径,且,将半圆绕点顺时针旋转,点旋转到点的位置,则图中阴影部分的面积为_____.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案
1.40°.
【详解】
解:根据扇形的面积计算公式可得:=π,
解得:n=40°,
即圆心角的度数为40°.
考点:扇形的面积计算.
2.2
【详解】
解:扇形的弧长==2πr,
∴圆锥的底面半径为r=2.
故答案为2.
3.B.
【解析】
试题分析:根据AE是⊙O的切线,A为切点,AB是⊙O的直径,可以先得出∠BAD为直角.再由同弧所对的圆周角等于它所对的圆心角的一半,求出∠B,从而得到∠ADB的度数.由题意得:∠BAD=90°,∵∠B=∠AOC=40°,∴∠ADB=90°-∠B=50°.故选B.
考点:圆的基本性质、切线的性质.
4.8或10.
【详解】
由勾股定理可知:
①当直角三角形的斜边长为16时,这个三角形的外接圆半径为8;
②当两条直角边长分别为16和12,则直角三角形的斜边长==20,因此这个三角形的外接圆半径为10.
综上所述:这个三角形的外接圆半径等于8或10.
故答案为10或8.
5.30π
【分析】
利用扇形的面积公式计算圆锥侧面积.
【详解】
解:圆锥侧面积=×2π×5×6=30π.
故答案为30π.
【点睛】
本题考查了圆锥的计算.圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
6.35
【分析】
如图(见解析),连接AD,先根据圆周角定理可得,从而可得,再根据圆周角定理可得,由此即可得.
【详解】
如图,连接AD
∵AB是⊙O的直径
∴,即
又由圆周角定理得:
∵
∴
故答案为:35.
【点睛】
本题考查了圆周角定理,熟记圆周角定理是解题关键.
7.50°
【解析】
试题分析:连接OA,
由题意得,∠AOB=2(∠ADC+∠BAC)=80°.
∵OA=OB(都是半径),
∴∠ABO=∠OAB=(180°﹣∠AOB)=50°.
8.
【解析】
试题分析:根据题意可得:阴影部分的面积等于半径为4的圆的四分之一的面积减去半径为2的圆的一半的面积.S=π×÷4-π×÷2=4π-2π=2π.
考点:圆的面积计算.
9.
【分析】
连接OC,根据同样只统计得到 ODCE是矩形,由矩形的性质得到∠ODC=90°.根据勾股定理得到OC=10,根据扇形的面积公式和矩形的面积公式即可得到结论.
【详解】
解:连接OC,
∵∠AOB=90°,四边形ODCE是平行四边形,
∴ ODCE是矩形,
∴∠ODC=90°.
∵OD=8,OE=6,
∴OC==10,
∴阴影部分图形的面积= -8×6=25π-48.
故答案为25π-48.
【点睛】
本题考查了扇形的面积的计算,矩形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
10.
【分析】
根据题意,作出合适的辅助线,然后根据图形可知阴影部分的面积是的面积与扇形OBC的面积之和再减去的面积,本题得以解决.
【详解】
解:作于点F,
在扇形AOB中,,半径OC交弦AB于点D,且.,
,,,
,
,,,,
,
阴影部分的面积是:,
故答案为.
【点睛】
本题考查扇形面积的计算,解答本题的关键是明确题意,利用数形结合的思想解答.
11.
【分析】
先根据题目条件计算出OD,CD的长度,判断为等边三角形,之后表示出阴影面积的计算公式进行计算即可.
【详解】
在中,
∴
∵
∴
∵
∴为等边三角形
∴
故答案为:
【点睛】
本题考查了阴影面积的计算,熟知不规则阴影面积的计算方法是解题的关键.
12.
【详解】
过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD sin30°=1,EB=AB﹣AE=2.
∴阴影部分的面积=平行四边形ABCD的面积-扇形ADE面积-三角形CBE的面积
=.
故答案为:.
13.44°
【分析】
首先连接OB,由点C在过点B的切线上,且OC⊥OA,根据等角的余角相等,易证得∠CBP=∠CPB,利用等腰三角形的性质解答即可.
【详解】
连接OB,
∵BC是⊙O的切线,
∴OB⊥BC,
∴∠OBA+∠CBP=90°,
∵OC⊥OA,
∴∠A+∠APO=90°,
∵OA=OB,∠OAB=22°,
∴∠OAB=∠OBA=22°,
∴∠APO=∠CBP=68°,
∵∠APO=∠CPB,
∴∠CPB=∠ABP=68°,
∴∠OCB=180°-68°-68°=44°,
故答案为44°
【点睛】
此题考查了切线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.
14.
【分析】
根据圆锥的底面半径得到圆锥的底面周长,也就是圆锥的侧面展开图的弧长,根据勾股定理得到圆锥的母线长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
【详解】
∵圆锥的底面半径为1,
∴圆锥的底面周长为2π,
∵圆锥的高是2,
∴圆锥的母线长为3,
设扇形的圆心角为n°,
∴=2π,
解得n=120.
即圆锥的侧面展开图中扇形的圆心角为120°.
故答案为120°.
【点睛】
本题考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
15.6
【分析】
根据图形可知,阴影部分的面积是半圆的面积与扇形的面积之和减去半圆的面积.
【详解】
由图可得,
图中阴影部分的面积为: ,
故答案为.
【点睛】
本题考查扇形面积的计算、旋转的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
绝密★启用前
九年级下册检测
第5章圆
第I卷(选择题)
一、填空题(共150分)
1.(本题10分)一个扇形的半径为3cm,面积为,则此扇形的圆心角为 .
2.(本题10分)用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是_____.
3.(本题10分)如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若AOC=80°,则ADB的度数为( )
A.40° B.50° C.60° D.20°
4.(本题10分)直角三角形的两边长分别为16和12,则此三角形的外接圆半径是_______.
5.(本题10分)圆锥底面圆半径为5,母线长为6,则圆锥侧面积等于_____.
6.(本题10分)如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2=_____°.
7.(本题10分)如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为______.
8.(本题10分)如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是______(结果保留)
9.(本题10分)如图,在扇形中,,分别是半径上的点,以为邻边的的顶点在上,若,则阴影部分图形的面积是________(结果保留).
10.(本题10分)如图,在扇形AOB中,,半径OC交弦AB于点D,且.若,则阴影部分的面积为_____.
11.(本题10分)如图所示的扇形中,,C为上一点,,连接,过C作的垂线交于点D,则图中阴影部分的面积为_______.
12.(本题10分)如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 ▲ (结果保留π).
13.(本题10分)如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=__________.
14.(本题10分)如图是一个圆锥的主视图,根据图中标出的数据(单位:),计算这个圆锥侧面展开图圆心角的度数为_______.
15.(本题10分)如图,为半圆的直径,且,将半圆绕点顺时针旋转,点旋转到点的位置,则图中阴影部分的面积为_____.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案
1.40°.
【详解】
解:根据扇形的面积计算公式可得:=π,
解得:n=40°,
即圆心角的度数为40°.
考点:扇形的面积计算.
2.2
【详解】
解:扇形的弧长==2πr,
∴圆锥的底面半径为r=2.
故答案为2.
3.B.
【解析】
试题分析:根据AE是⊙O的切线,A为切点,AB是⊙O的直径,可以先得出∠BAD为直角.再由同弧所对的圆周角等于它所对的圆心角的一半,求出∠B,从而得到∠ADB的度数.由题意得:∠BAD=90°,∵∠B=∠AOC=40°,∴∠ADB=90°-∠B=50°.故选B.
考点:圆的基本性质、切线的性质.
4.8或10.
【详解】
由勾股定理可知:
①当直角三角形的斜边长为16时,这个三角形的外接圆半径为8;
②当两条直角边长分别为16和12,则直角三角形的斜边长==20,因此这个三角形的外接圆半径为10.
综上所述:这个三角形的外接圆半径等于8或10.
故答案为10或8.
5.30π
【分析】
利用扇形的面积公式计算圆锥侧面积.
【详解】
解:圆锥侧面积=×2π×5×6=30π.
故答案为30π.
【点睛】
本题考查了圆锥的计算.圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
6.35
【分析】
如图(见解析),连接AD,先根据圆周角定理可得,从而可得,再根据圆周角定理可得,由此即可得.
【详解】
如图,连接AD
∵AB是⊙O的直径
∴,即
又由圆周角定理得:
∵
∴
故答案为:35.
【点睛】
本题考查了圆周角定理,熟记圆周角定理是解题关键.
7.50°
【解析】
试题分析:连接OA,
由题意得,∠AOB=2(∠ADC+∠BAC)=80°.
∵OA=OB(都是半径),
∴∠ABO=∠OAB=(180°﹣∠AOB)=50°.
8.
【解析】
试题分析:根据题意可得:阴影部分的面积等于半径为4的圆的四分之一的面积减去半径为2的圆的一半的面积.S=π×÷4-π×÷2=4π-2π=2π.
考点:圆的面积计算.
9.
【分析】
连接OC,根据同样只统计得到 ODCE是矩形,由矩形的性质得到∠ODC=90°.根据勾股定理得到OC=10,根据扇形的面积公式和矩形的面积公式即可得到结论.
【详解】
解:连接OC,
∵∠AOB=90°,四边形ODCE是平行四边形,
∴ ODCE是矩形,
∴∠ODC=90°.
∵OD=8,OE=6,
∴OC==10,
∴阴影部分图形的面积= -8×6=25π-48.
故答案为25π-48.
【点睛】
本题考查了扇形的面积的计算,矩形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
10.
【分析】
根据题意,作出合适的辅助线,然后根据图形可知阴影部分的面积是的面积与扇形OBC的面积之和再减去的面积,本题得以解决.
【详解】
解:作于点F,
在扇形AOB中,,半径OC交弦AB于点D,且.,
,,,
,
,,,,
,
阴影部分的面积是:,
故答案为.
【点睛】
本题考查扇形面积的计算,解答本题的关键是明确题意,利用数形结合的思想解答.
11.
【分析】
先根据题目条件计算出OD,CD的长度,判断为等边三角形,之后表示出阴影面积的计算公式进行计算即可.
【详解】
在中,
∴
∵
∴
∵
∴为等边三角形
∴
故答案为:
【点睛】
本题考查了阴影面积的计算,熟知不规则阴影面积的计算方法是解题的关键.
12.
【详解】
过D点作DF⊥AB于点F.
∵AD=2,AB=4,∠A=30°,
∴DF=AD sin30°=1,EB=AB﹣AE=2.
∴阴影部分的面积=平行四边形ABCD的面积-扇形ADE面积-三角形CBE的面积
=.
故答案为:.
13.44°
【分析】
首先连接OB,由点C在过点B的切线上,且OC⊥OA,根据等角的余角相等,易证得∠CBP=∠CPB,利用等腰三角形的性质解答即可.
【详解】
连接OB,
∵BC是⊙O的切线,
∴OB⊥BC,
∴∠OBA+∠CBP=90°,
∵OC⊥OA,
∴∠A+∠APO=90°,
∵OA=OB,∠OAB=22°,
∴∠OAB=∠OBA=22°,
∴∠APO=∠CBP=68°,
∵∠APO=∠CPB,
∴∠CPB=∠ABP=68°,
∴∠OCB=180°-68°-68°=44°,
故答案为44°
【点睛】
此题考查了切线的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.
14.
【分析】
根据圆锥的底面半径得到圆锥的底面周长,也就是圆锥的侧面展开图的弧长,根据勾股定理得到圆锥的母线长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
【详解】
∵圆锥的底面半径为1,
∴圆锥的底面周长为2π,
∵圆锥的高是2,
∴圆锥的母线长为3,
设扇形的圆心角为n°,
∴=2π,
解得n=120.
即圆锥的侧面展开图中扇形的圆心角为120°.
故答案为120°.
【点睛】
本题考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
15.6
【分析】
根据图形可知,阴影部分的面积是半圆的面积与扇形的面积之和减去半圆的面积.
【详解】
由图可得,
图中阴影部分的面积为: ,
故答案为.
【点睛】
本题考查扇形面积的计算、旋转的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
