九年级第二学期圆选择题题训练(含解析)
文档属性
| 名称 | 九年级第二学期圆选择题题训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 466.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
绝密★启用前
九年级下册检测
第5章圆
第I卷(选择题)
每题3分,共150分
一、单选题(共150分)
1.(本题10分)如图,点A,B,C,D四点均在圆O上,∠AOD=68°,AO//DC,则∠B的度数为( )
A.40° B.60° C.56° D.68°
2.(本题10分)如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm B. cm C.2.5cm D. cm
3.(本题10分)如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
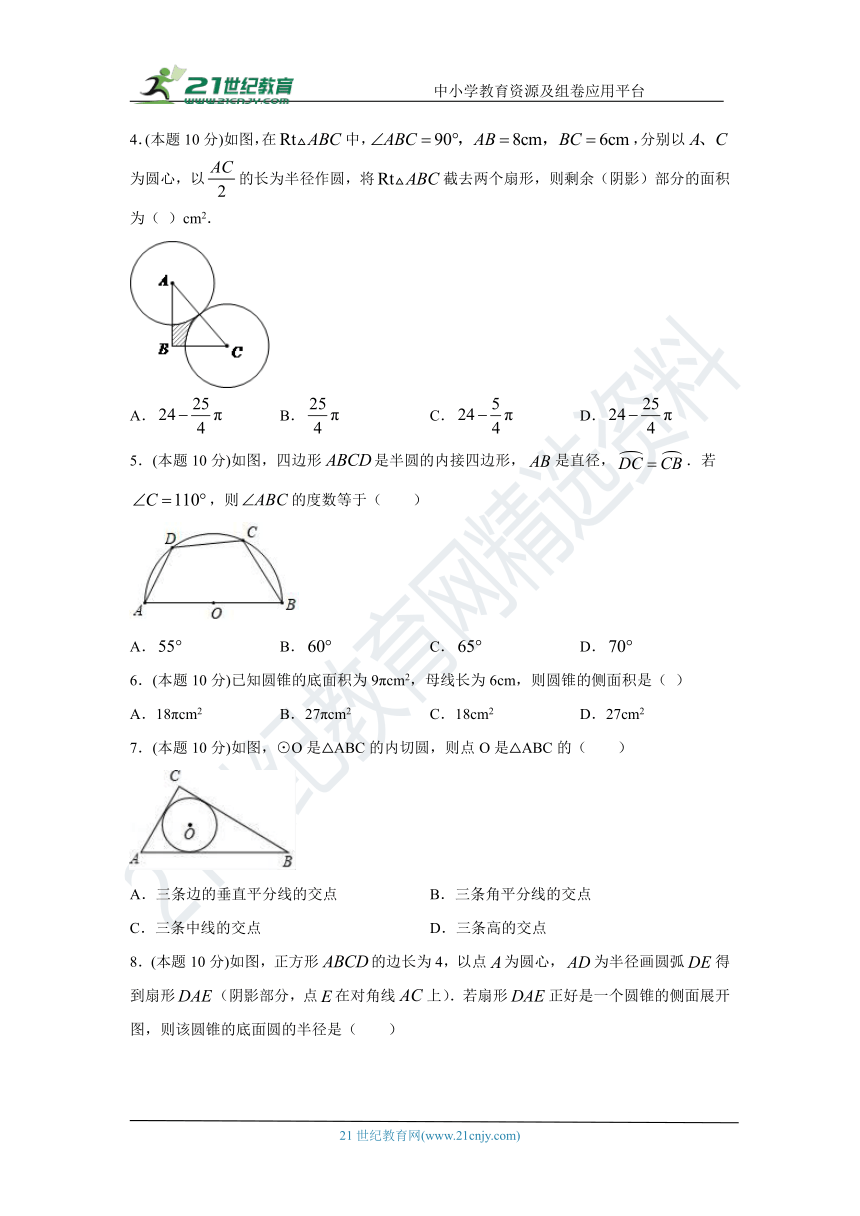
4.(本题10分)如图,在中,,分别以为圆心,以的长为半径作圆,将截去两个扇形,则剩余(阴影)部分的面积为( )cm2.
A. B. C. D.
5.(本题10分)如图,四边形是半圆的内接四边形,是直径,.若,则的度数等于( )
A. B. C. D.
6.(本题10分)已知圆锥的底面积为9πcm2,母线长为6cm,则圆锥的侧面积是( )
A.18πcm2 B.27πcm2 C.18cm2 D.27cm2
7.(本题10分)如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
8.(本题10分)如图,正方形的边长为4,以点为圆心,为半径画圆弧得到扇形(阴影部分,点在对角线上).若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A. B.1 C. D.
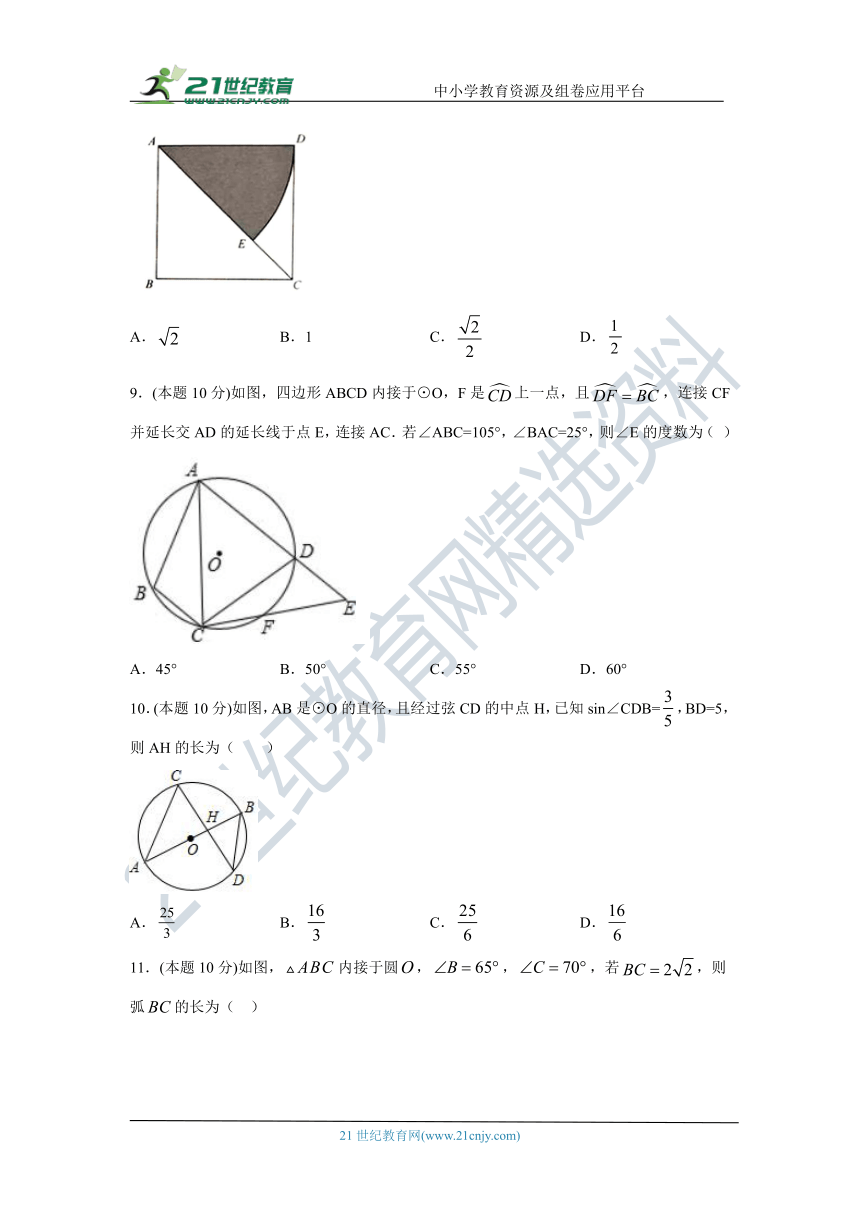
9.(本题10分)如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
10.(本题10分)如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长为( )
A. B. C. D.
11.(本题10分)如图,内接于圆,,,若,则弧的长为( )
A. B. C. D.
12.(本题10分)如图,分别以等边三角形的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若,则莱洛三角形的面积(即阴影部分的面积)( ).
A. B. C. D.
13.(本题10分)如图所示的网格由边长相同的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则△ABC的外心是( )
A.点D B.点E C.点F D.点G
14.(本题10分)如图,四边形内接于,,则的度数( )
A. B.
C. D.
15.(本题10分)如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°.则∠BOC等于( )
A.125° B.120° C.115° D.100°
参考答案
1.C
【分析】
连接AD,先根据等腰三角形的性质求出∠ODA,再根据平行线的性质求出∠ODC,最后根据圆内接四边形的性质计算即可.
【详解】
解:连接AD,
∵∠AOD=68°,OA=OD,
∴∠ODA=∠OAD=56°,
∵AO∥DC,
∴∠ODC=∠AOD=68°,
∴∠ADC=124°,
∵点A、B、C、D四个点都在⊙O上,
∴∠B=180°-∠ADC=56°,
故选C.
【点睛】
本题考查的是圆内接四边形的性质、等腰三角形的性质、平行线的性质,掌握圆内接四边形的对角互补是解题的关键.
2.D
【解析】
分析:根据垂径定理得出OE的长,进而利用勾股定理得出BC的长,再利用相似三角形的判定和性质解答即可.
详解:连接OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm.
在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2
解得:OE=3,
∴OB=3+2=5,
∴EC=5+3=8.
在Rt△EBC中,BC=.
∵OF⊥BC,
∴∠OFC=∠CEB=90°.
∵∠C=∠C,
∴△OFC∽△BEC,
∴,即,
解得:OF=.
故选D.
点睛:本题考查了垂径定理,关键是根据垂径定理得出OE的长.
3.C
【解析】
试题分析:连结CD,可得CD为直径,在Rt△OCD中,CD=6,OC=2,根据勾股定理求得OD=4
所以tan∠CDO=,由圆周角定理得,∠OBC=∠CDO,则tan∠OBC=,故答案选C.
考点:圆周角定理;锐角三角函数的定义.
4.A
【详解】
解:如图,
∵Rt△ABC中,∠ABC=90°,AB=8,BC=6,
,△ABC的面积是:,
,
故阴影部分的面积是:,
故选A.
5.A
【分析】
连接AC,根据圆内接四边形的性质求出∠DAB,根据圆周角定理求出∠ACB、∠CAB,计算即可.
【详解】
连接AC,
∵四边形ABCD是半圆的内接四边形,
∴∠DAB=180°-∠C=70°,
∵,
∴∠CAB=∠DAB=35°,
∵AB是直径,
∴∠ACB=90°,
∴∠ABC=90°-∠CAB=55°,
故选A.
【点睛】
本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
6.A
【解析】
试题分析:∵圆锥的底面积为9πcm2,
∴圆锥的底面半径为3,
∵母线长为6cm,
∴侧面积为3×6π=18πcm2,
故选A;
考点:圆锥的计算.
7.B
【详解】
解:内心到三角形三边距离相等,到角的两边距离相等的点在这个角的角平分线上,
故选:B.
【点睛】
本题考查内心的定义.
8.D
【分析】
根据题意,扇形ADE中弧DE的长即为圆锥底面圆的周长,即通过计算弧DE的长,再结合圆的周长公式进行计算即可得解.
【详解】
∵正方形的边长为4
∴
∵是正方形的对角线
∴
∴
∴圆锥底面周长为,解得
∴该圆锥的底面圆的半径是,
故选:D.
【点睛】
本题主要考查了扇形的弧长公式,圆的周长公式,正方形的性质以及圆锥的相关知识点,熟练掌握弧长公式及圆的周长公式是解决本题的关键.
9.B
【分析】
先根据圆内接四边形的性质求出∠ADC的度数,再由圆周角定理得出∠DCE的度数,根据三角形外角的性质即可得出结论.
【详解】
∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
【点睛】
本题考查圆内接四边形的性质,圆周角定理.圆内接四边形对角互补.在同圆或等圆中,同弧或等弧所对的圆心角相等,而同弧所对的圆周角等于圆心角的一半,所以在同圆或等圆中,同弧或等弧所对的圆周角相等.
10.B
【解析】
【分析】连接OD,由垂径定理得出AB⊥CD,由三角函数求出BH=3,由勾股定理得出DH==4,设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得出方程,解方程即可.
【详解】连接OD,如图所示:
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=∠BHD=90°,
∵sin∠CDB=,BD=5,
∴BH=3,
∴DH==4,
设OH=x,则OD=OB=x+3,
在Rt△ODH中,由勾股定理得:x2+42=(x+3)2,
解得:x=,
∴OH=,
∴AH=OA+OH=+3+=,
故选B.
【点睛】本题考查了垂径定理、勾股定理以及三角函数等知识,正确添加辅助线,熟练应用垂径定理、灵活运用数形结合思想是解题的关键.
11.A
【分析】
连接OB,OC.首先证明△OBC是等腰直角三角形,求出OB即可解决问题.
【详解】
连接OB,OC.
∵∠A=180°-∠ABC-∠ACB=180°-65°-70°=45°,
∴∠BOC=90°,
∵BC=2,
∴OB=OC=2,
∴的长为=π,
故选A.
【点睛】
本题考查圆周角定理,弧长公式,等腰直角三角形的性质的等知识,解题的关键是熟练掌握基本知识
12.B
【分析】
图中三角形的面积是由三块相同的扇形叠加而成,其面积=三块扇形的面积相加,再减去两个等边三角形的面积,分别求出即可.
【详解】
过A点作于点D,
∵是等边三角形,
∴,,
∵,
∴,,
∴的面积为:,
,
∴莱洛三角形的面积.
故选:B.
【点睛】
本题考查了等边三角形的性质和扇形面积的计算,能根据图形得出莱洛三角形的面积=3块扇形面积加起来减去两个等边三角形的面积是解答本题的关键.
13.A
【分析】
根据三角形三边中垂线相交于一点,这一点叫做它的外心,据此解答即可.
【详解】
根据图形可知,直线DG是△ABC的BC边上的中垂线,点D在△ABC的AB边上的中垂线上,
∴点D是△ABC外心.
故选:A.
【点睛】
本题主要考查了三角形的外心的定义,注意:三角形三边中垂线相交于一点,这一点是此三角形的外心.
14.A
【分析】
根据圆内接四边形的性质可得∠EDB=∠A=,然后根据同弧所对圆周角和圆心角的关系可求解.
【详解】
解:∵四边形内接于,,
∴∠EDB=∠A=,
∴,
故选A.
【点睛】
本题主要考查圆内接四边形的性质及圆周角、圆心角的关系,熟练掌握圆内接四边形的性质及圆周角、圆心角的关系是解题的关键.
15.C
【分析】
根据三角形△ABC是内切圆,故知道BO、CO的角平分线,求出 ,利用三角形内角和定理,便可找到答案.
【详解】
解: ⊙O是△ABC的内切圆
∴BO、CO分别平分∠ABC、∠ACB
又∠ABC=50°,∠ACB=80°
∴=25°、°
∴180°=115°
故选:C.
【点睛】
本题考查内切圆的定义,利用三角形内角和求角的度数,关键在于理解内切圆的定义.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
绝密★启用前
九年级下册检测
第5章圆
第I卷(选择题)
每题3分,共150分
一、单选题(共150分)
1.(本题10分)如图,点A,B,C,D四点均在圆O上,∠AOD=68°,AO//DC,则∠B的度数为( )
A.40° B.60° C.56° D.68°
2.(本题10分)如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm B. cm C.2.5cm D. cm
3.(本题10分)如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
4.(本题10分)如图,在中,,分别以为圆心,以的长为半径作圆,将截去两个扇形,则剩余(阴影)部分的面积为( )cm2.
A. B. C. D.
5.(本题10分)如图,四边形是半圆的内接四边形,是直径,.若,则的度数等于( )
A. B. C. D.
6.(本题10分)已知圆锥的底面积为9πcm2,母线长为6cm,则圆锥的侧面积是( )
A.18πcm2 B.27πcm2 C.18cm2 D.27cm2
7.(本题10分)如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
8.(本题10分)如图,正方形的边长为4,以点为圆心,为半径画圆弧得到扇形(阴影部分,点在对角线上).若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A. B.1 C. D.
9.(本题10分)如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
10.(本题10分)如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长为( )
A. B. C. D.
11.(本题10分)如图,内接于圆,,,若,则弧的长为( )
A. B. C. D.
12.(本题10分)如图,分别以等边三角形的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若,则莱洛三角形的面积(即阴影部分的面积)( ).
A. B. C. D.
13.(本题10分)如图所示的网格由边长相同的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则△ABC的外心是( )
A.点D B.点E C.点F D.点G
14.(本题10分)如图,四边形内接于,,则的度数( )
A. B.
C. D.
15.(本题10分)如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°.则∠BOC等于( )
A.125° B.120° C.115° D.100°
参考答案
1.C
【分析】
连接AD,先根据等腰三角形的性质求出∠ODA,再根据平行线的性质求出∠ODC,最后根据圆内接四边形的性质计算即可.
【详解】
解:连接AD,
∵∠AOD=68°,OA=OD,
∴∠ODA=∠OAD=56°,
∵AO∥DC,
∴∠ODC=∠AOD=68°,
∴∠ADC=124°,
∵点A、B、C、D四个点都在⊙O上,
∴∠B=180°-∠ADC=56°,
故选C.
【点睛】
本题考查的是圆内接四边形的性质、等腰三角形的性质、平行线的性质,掌握圆内接四边形的对角互补是解题的关键.
2.D
【解析】
分析:根据垂径定理得出OE的长,进而利用勾股定理得出BC的长,再利用相似三角形的判定和性质解答即可.
详解:连接OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm.
在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2
解得:OE=3,
∴OB=3+2=5,
∴EC=5+3=8.
在Rt△EBC中,BC=.
∵OF⊥BC,
∴∠OFC=∠CEB=90°.
∵∠C=∠C,
∴△OFC∽△BEC,
∴,即,
解得:OF=.
故选D.
点睛:本题考查了垂径定理,关键是根据垂径定理得出OE的长.
3.C
【解析】
试题分析:连结CD,可得CD为直径,在Rt△OCD中,CD=6,OC=2,根据勾股定理求得OD=4
所以tan∠CDO=,由圆周角定理得,∠OBC=∠CDO,则tan∠OBC=,故答案选C.
考点:圆周角定理;锐角三角函数的定义.
4.A
【详解】
解:如图,
∵Rt△ABC中,∠ABC=90°,AB=8,BC=6,
,△ABC的面积是:,
,
故阴影部分的面积是:,
故选A.
5.A
【分析】
连接AC,根据圆内接四边形的性质求出∠DAB,根据圆周角定理求出∠ACB、∠CAB,计算即可.
【详解】
连接AC,
∵四边形ABCD是半圆的内接四边形,
∴∠DAB=180°-∠C=70°,
∵,
∴∠CAB=∠DAB=35°,
∵AB是直径,
∴∠ACB=90°,
∴∠ABC=90°-∠CAB=55°,
故选A.
【点睛】
本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
6.A
【解析】
试题分析:∵圆锥的底面积为9πcm2,
∴圆锥的底面半径为3,
∵母线长为6cm,
∴侧面积为3×6π=18πcm2,
故选A;
考点:圆锥的计算.
7.B
【详解】
解:内心到三角形三边距离相等,到角的两边距离相等的点在这个角的角平分线上,
故选:B.
【点睛】
本题考查内心的定义.
8.D
【分析】
根据题意,扇形ADE中弧DE的长即为圆锥底面圆的周长,即通过计算弧DE的长,再结合圆的周长公式进行计算即可得解.
【详解】
∵正方形的边长为4
∴
∵是正方形的对角线
∴
∴
∴圆锥底面周长为,解得
∴该圆锥的底面圆的半径是,
故选:D.
【点睛】
本题主要考查了扇形的弧长公式,圆的周长公式,正方形的性质以及圆锥的相关知识点,熟练掌握弧长公式及圆的周长公式是解决本题的关键.
9.B
【分析】
先根据圆内接四边形的性质求出∠ADC的度数,再由圆周角定理得出∠DCE的度数,根据三角形外角的性质即可得出结论.
【详解】
∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
【点睛】
本题考查圆内接四边形的性质,圆周角定理.圆内接四边形对角互补.在同圆或等圆中,同弧或等弧所对的圆心角相等,而同弧所对的圆周角等于圆心角的一半,所以在同圆或等圆中,同弧或等弧所对的圆周角相等.
10.B
【解析】
【分析】连接OD,由垂径定理得出AB⊥CD,由三角函数求出BH=3,由勾股定理得出DH==4,设OH=x,则OD=OB=x+3,在Rt△ODH中,由勾股定理得出方程,解方程即可.
【详解】连接OD,如图所示:
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=∠BHD=90°,
∵sin∠CDB=,BD=5,
∴BH=3,
∴DH==4,
设OH=x,则OD=OB=x+3,
在Rt△ODH中,由勾股定理得:x2+42=(x+3)2,
解得:x=,
∴OH=,
∴AH=OA+OH=+3+=,
故选B.
【点睛】本题考查了垂径定理、勾股定理以及三角函数等知识,正确添加辅助线,熟练应用垂径定理、灵活运用数形结合思想是解题的关键.
11.A
【分析】
连接OB,OC.首先证明△OBC是等腰直角三角形,求出OB即可解决问题.
【详解】
连接OB,OC.
∵∠A=180°-∠ABC-∠ACB=180°-65°-70°=45°,
∴∠BOC=90°,
∵BC=2,
∴OB=OC=2,
∴的长为=π,
故选A.
【点睛】
本题考查圆周角定理,弧长公式,等腰直角三角形的性质的等知识,解题的关键是熟练掌握基本知识
12.B
【分析】
图中三角形的面积是由三块相同的扇形叠加而成,其面积=三块扇形的面积相加,再减去两个等边三角形的面积,分别求出即可.
【详解】
过A点作于点D,
∵是等边三角形,
∴,,
∵,
∴,,
∴的面积为:,
,
∴莱洛三角形的面积.
故选:B.
【点睛】
本题考查了等边三角形的性质和扇形面积的计算,能根据图形得出莱洛三角形的面积=3块扇形面积加起来减去两个等边三角形的面积是解答本题的关键.
13.A
【分析】
根据三角形三边中垂线相交于一点,这一点叫做它的外心,据此解答即可.
【详解】
根据图形可知,直线DG是△ABC的BC边上的中垂线,点D在△ABC的AB边上的中垂线上,
∴点D是△ABC外心.
故选:A.
【点睛】
本题主要考查了三角形的外心的定义,注意:三角形三边中垂线相交于一点,这一点是此三角形的外心.
14.A
【分析】
根据圆内接四边形的性质可得∠EDB=∠A=,然后根据同弧所对圆周角和圆心角的关系可求解.
【详解】
解:∵四边形内接于,,
∴∠EDB=∠A=,
∴,
故选A.
【点睛】
本题主要考查圆内接四边形的性质及圆周角、圆心角的关系,熟练掌握圆内接四边形的性质及圆周角、圆心角的关系是解题的关键.
15.C
【分析】
根据三角形△ABC是内切圆,故知道BO、CO的角平分线,求出 ,利用三角形内角和定理,便可找到答案.
【详解】
解: ⊙O是△ABC的内切圆
∴BO、CO分别平分∠ABC、∠ACB
又∠ABC=50°,∠ACB=80°
∴=25°、°
∴180°=115°
故选:C.
【点睛】
本题考查内切圆的定义,利用三角形内角和求角的度数,关键在于理解内切圆的定义.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
