搭配-人教版数学三年级下册第八单元教学课件(共32张PPT)
文档属性
| 名称 | 搭配-人教版数学三年级下册第八单元教学课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 16:12:29 | ||
图片预览







文档简介
(共32张PPT)
第1课时 搭配(1)
义务教育人教版三年级下册
8 数学广角——搭配(二)
新课导入
下面三个字可以有多少种不同的组合
孙 行 者
孙行者
行孙者
者行孙
孙者行
行者孙
者孙行
答:可以有6种不同的组合。
探究新知
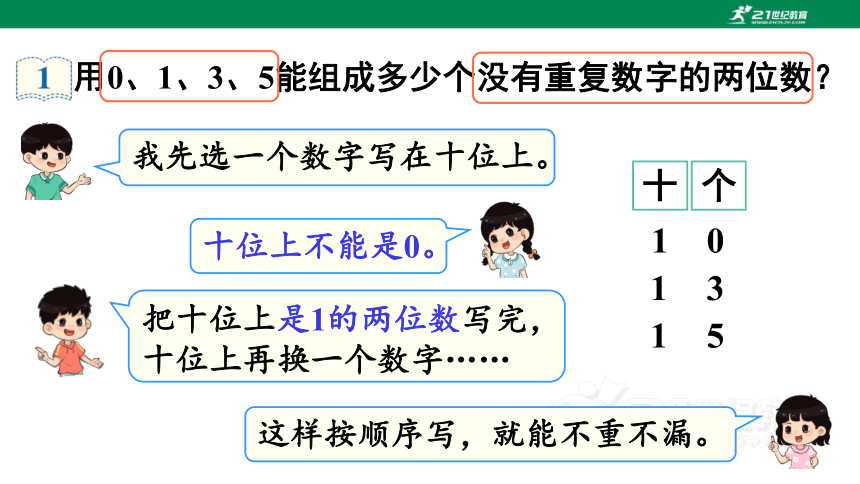
用0、1、3、5能组成多少个没有重复数字的两位数?
自学提示:
(1)想一想:十位上的数字可以是哪些?
(2)说一说:怎样写不重不漏?
用0、1、3、5能组成多少个没有重复数字的两位数?
十
个
0
1
3
1
5
我先选一个数字写在十位上。
十位上不能是0。
1
把十位上是1的两位数写完,十位上再换一个数字……
这样按顺序写,就能不重不漏。
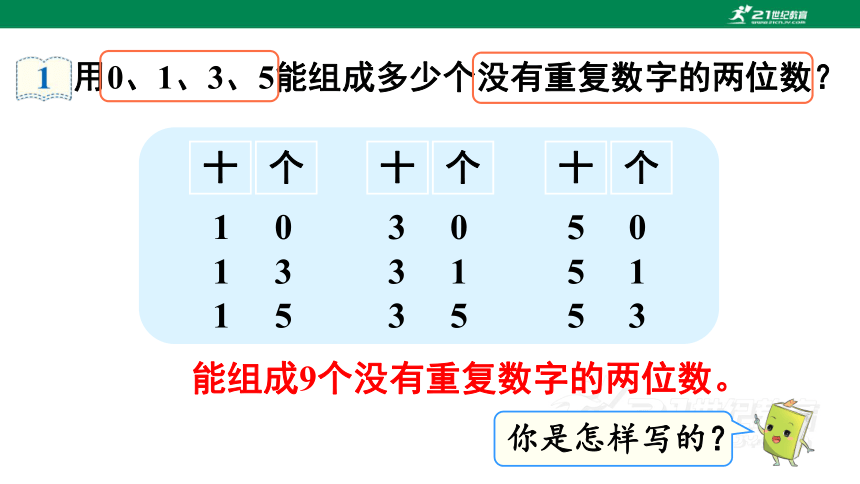
用0、1、3、5能组成多少个没有重复数字的两位数?
十
个
0
1
3
1
5
1
十
个
0
3
1
3
5
3
十
个
0
5
1
5
3
5
能组成9个没有重复数字的两位数。
你是怎样写的?
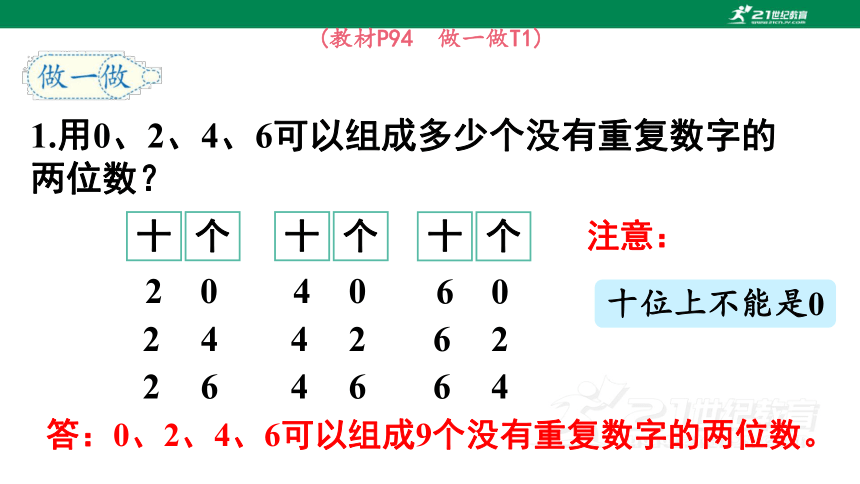
(教材P94 做一做T1)
1.用0、2、4、6可以组成多少个没有重复数字的两位数?
十
个
0
2
4
2
6
2
十
个
0
4
2
4
6
4
十
个
0
6
2
6
4
6
十位上不能是0
注意:
答:0、2、4、6可以组成9个没有重复数字的两位数。
(教材P94 做一做T2)
2.把5块巧克力全部分给小丽、小明、小红,每人至少分到1块。有多少种分法?
小丽
小明
小红
1
2
3
2
2
3
1
1
2
2
1
1
1
1
3
1
1
2
答:有6种分法。
巩固运用
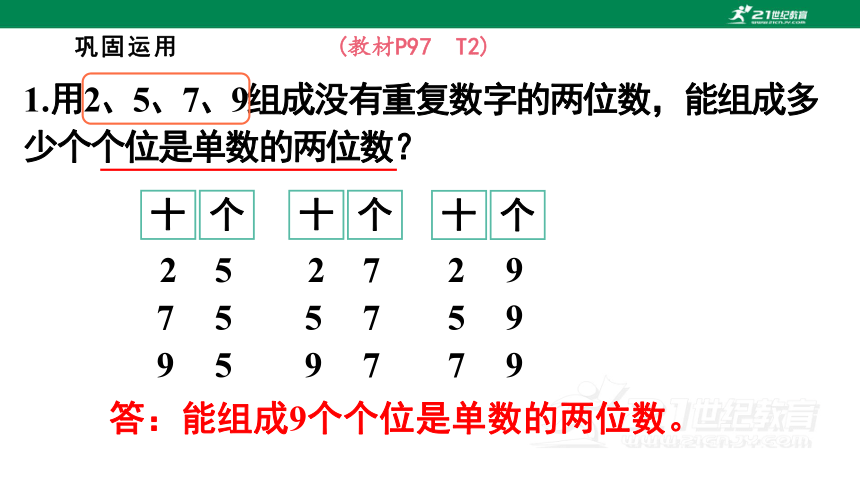
(教材P97 T2)
1.用2、5、7、9组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
十
个
5
7
5
9
5
2
十
个
7
5
7
9
7
2
十
个
9
5
9
7
9
2
答:能组成9个个位是单数的两位数。
(教材P97 T3)
2.从1、2中任选一个数作分子,从3、4、5中任选一个数作分母,一共可以组成多少个分数?
分子 1 2
分母 3 4 5 3 4 5
答:一共可以组成6个分数。
情境导入
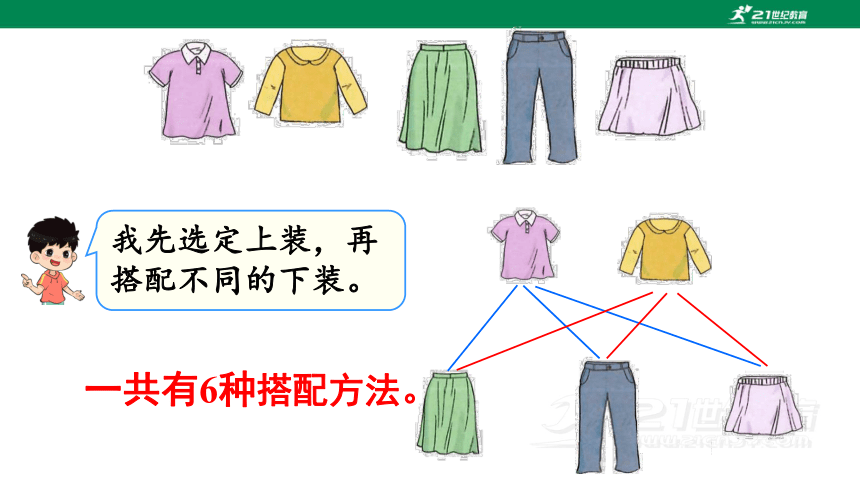
周末,我要去参加同学的生日会,大家能帮我搭配一下衣服吗
探究新知
一共有多少种搭配方法?
每次上装和下装只能各选1件。
一共有6种搭配方法。
我先选定上装,再搭配不同的下装。
一共有6种搭配方法。
我先选定下装,再搭配不同的上装。
我用 表示上装, 表示下装。
每件上装可以与3件下装搭配,这样就有3种穿法,有2件上装,一共有6种搭配方法。
我用A表示上装,B表示下装。
一共有6种搭配方法。
A1 A2
B1 B2 B3
2×3=6(种)
A1 A2
B1 B2 B3
比较一下,你更喜欢哪种方法?
先固定其中一种,再按顺序搭配。
搭配要有序,才能不重复、不遗漏。
(教材P95 做一做T1)
2
4
9
3
6
8
1.拉动纸条,看看可以组成哪些两位数,并记录下来。
2
4
9
3
6
8
23
26
28
3
6
8
2
4
9
23
26
28
43
46
48
3
6
8
2
4
9
93
96
98
23
26
28
43
46
48
(教材P95 做一做T2)
2.从下面的饮品和主食中各选1样,有多少种
不同的搭配?
答:有8种不同的搭配。
豆浆
牛奶
发糕
包子
烧饼
馒头
1.
答:一共要拍8张照片。
2×4=8(张)
一共要拍多少张照片?
我们每个人分别和冰墩墩、雪容融拍一张照片。
巩固运用
(教材P97 T4)
(教材P98 T5)
2.右图中一共有多少个长方形?
①由一个长方形组成的:
4个
②由两个长方形组成的:
4个
③由四个长方形组成的:
1个
4+4+1=9(个)
答:一共有9个长方形。
复习导入
把下面3个玩具按不同的位置摆放,有( )种摆法。
6
探究新知
三年级4个班进行足球比赛。每2个班踢一场,一共要踢多少场?
1—2
1—3
1—4
2—1
2—3
2—4
3—1
3—2
3—4
3+2+1=6,一共要踢 6 场。
我先确定1班要踢 3场,再确定 2 班要……
1班
2班
3班
4班
①
②
③
④
⑤
⑥
一共连了6条线,说明一共要踢6场。
把4个班摆成一排,再把每个班与其他班分别连上线。
1班
2班
3班
4班
①
④
⑤
⑥
③
②
把4个班摆成正方形或长方形,再把任意2个班直接连上线。
一共连了6条线,说明一共要踢6场。
(教材P96 做一做T1)
1.有 5 个人,每 2 个人握一次手,一共要握多少次手?
⑤
②
①
③
④
⑥
⑦
⑧
⑨
⑩
答:一共要握10次手。
1
2
3
4
5
(教材P96 做一做T2)
2.每次取 2 枚。
我取出了6角。
取出的钱共有哪几种情况?请写出来。
1元零5分
1元5角
1元1角
5角5分
1角5分
6角
答:取出的钱共有 6 种情况。
巩固运用
(教材P98 T7)
1.甲、乙、丙、丁4个人参加乒乓球小组赛,每2个人比赛一场,一共要比赛多少场?
①
②
③
④
⑤
⑥
甲
乙
丙
丁
答:一共要比赛6场。
2.
(1)小明想从中任选2本书,共有多少种选法?
①
②
③
④
①②
①③
①④
②③
②④
③④
答:共有6种选法。
(教材P98 T8)
(2)小明想选1本《数学家的故事》和1本其他的书,分别送给小红和小丽,共有多少种送法?
①
②
③
④
选出的2本书可以是①②、①③、①④,有3种选法。
小红 小丽
① ②
② ①
小红 小丽
① ③
③ ①
小红 小丽
① ④
④ ①
答:共有6种送法。
第1课时 搭配(1)
义务教育人教版三年级下册
8 数学广角——搭配(二)
新课导入
下面三个字可以有多少种不同的组合
孙 行 者
孙行者
行孙者
者行孙
孙者行
行者孙
者孙行
答:可以有6种不同的组合。
探究新知
用0、1、3、5能组成多少个没有重复数字的两位数?
自学提示:
(1)想一想:十位上的数字可以是哪些?
(2)说一说:怎样写不重不漏?
用0、1、3、5能组成多少个没有重复数字的两位数?
十
个
0
1
3
1
5
我先选一个数字写在十位上。
十位上不能是0。
1
把十位上是1的两位数写完,十位上再换一个数字……
这样按顺序写,就能不重不漏。
用0、1、3、5能组成多少个没有重复数字的两位数?
十
个
0
1
3
1
5
1
十
个
0
3
1
3
5
3
十
个
0
5
1
5
3
5
能组成9个没有重复数字的两位数。
你是怎样写的?
(教材P94 做一做T1)
1.用0、2、4、6可以组成多少个没有重复数字的两位数?
十
个
0
2
4
2
6
2
十
个
0
4
2
4
6
4
十
个
0
6
2
6
4
6
十位上不能是0
注意:
答:0、2、4、6可以组成9个没有重复数字的两位数。
(教材P94 做一做T2)
2.把5块巧克力全部分给小丽、小明、小红,每人至少分到1块。有多少种分法?
小丽
小明
小红
1
2
3
2
2
3
1
1
2
2
1
1
1
1
3
1
1
2
答:有6种分法。
巩固运用
(教材P97 T2)
1.用2、5、7、9组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
十
个
5
7
5
9
5
2
十
个
7
5
7
9
7
2
十
个
9
5
9
7
9
2
答:能组成9个个位是单数的两位数。
(教材P97 T3)
2.从1、2中任选一个数作分子,从3、4、5中任选一个数作分母,一共可以组成多少个分数?
分子 1 2
分母 3 4 5 3 4 5
答:一共可以组成6个分数。
情境导入
周末,我要去参加同学的生日会,大家能帮我搭配一下衣服吗
探究新知
一共有多少种搭配方法?
每次上装和下装只能各选1件。
一共有6种搭配方法。
我先选定上装,再搭配不同的下装。
一共有6种搭配方法。
我先选定下装,再搭配不同的上装。
我用 表示上装, 表示下装。
每件上装可以与3件下装搭配,这样就有3种穿法,有2件上装,一共有6种搭配方法。
我用A表示上装,B表示下装。
一共有6种搭配方法。
A1 A2
B1 B2 B3
2×3=6(种)
A1 A2
B1 B2 B3
比较一下,你更喜欢哪种方法?
先固定其中一种,再按顺序搭配。
搭配要有序,才能不重复、不遗漏。
(教材P95 做一做T1)
2
4
9
3
6
8
1.拉动纸条,看看可以组成哪些两位数,并记录下来。
2
4
9
3
6
8
23
26
28
3
6
8
2
4
9
23
26
28
43
46
48
3
6
8
2
4
9
93
96
98
23
26
28
43
46
48
(教材P95 做一做T2)
2.从下面的饮品和主食中各选1样,有多少种
不同的搭配?
答:有8种不同的搭配。
豆浆
牛奶
发糕
包子
烧饼
馒头
1.
答:一共要拍8张照片。
2×4=8(张)
一共要拍多少张照片?
我们每个人分别和冰墩墩、雪容融拍一张照片。
巩固运用
(教材P97 T4)
(教材P98 T5)
2.右图中一共有多少个长方形?
①由一个长方形组成的:
4个
②由两个长方形组成的:
4个
③由四个长方形组成的:
1个
4+4+1=9(个)
答:一共有9个长方形。
复习导入
把下面3个玩具按不同的位置摆放,有( )种摆法。
6
探究新知
三年级4个班进行足球比赛。每2个班踢一场,一共要踢多少场?
1—2
1—3
1—4
2—1
2—3
2—4
3—1
3—2
3—4
3+2+1=6,一共要踢 6 场。
我先确定1班要踢 3场,再确定 2 班要……
1班
2班
3班
4班
①
②
③
④
⑤
⑥
一共连了6条线,说明一共要踢6场。
把4个班摆成一排,再把每个班与其他班分别连上线。
1班
2班
3班
4班
①
④
⑤
⑥
③
②
把4个班摆成正方形或长方形,再把任意2个班直接连上线。
一共连了6条线,说明一共要踢6场。
(教材P96 做一做T1)
1.有 5 个人,每 2 个人握一次手,一共要握多少次手?
⑤
②
①
③
④
⑥
⑦
⑧
⑨
⑩
答:一共要握10次手。
1
2
3
4
5
(教材P96 做一做T2)
2.每次取 2 枚。
我取出了6角。
取出的钱共有哪几种情况?请写出来。
1元零5分
1元5角
1元1角
5角5分
1角5分
6角
答:取出的钱共有 6 种情况。
巩固运用
(教材P98 T7)
1.甲、乙、丙、丁4个人参加乒乓球小组赛,每2个人比赛一场,一共要比赛多少场?
①
②
③
④
⑤
⑥
甲
乙
丙
丁
答:一共要比赛6场。
2.
(1)小明想从中任选2本书,共有多少种选法?
①
②
③
④
①②
①③
①④
②③
②④
③④
答:共有6种选法。
(教材P98 T8)
(2)小明想选1本《数学家的故事》和1本其他的书,分别送给小红和小丽,共有多少种送法?
①
②
③
④
选出的2本书可以是①②、①③、①④,有3种选法。
小红 小丽
① ②
② ①
小红 小丽
① ③
③ ①
小红 小丽
① ④
④ ①
答:共有6种送法。
