基本不等式(两课时)
图片预览





文档简介
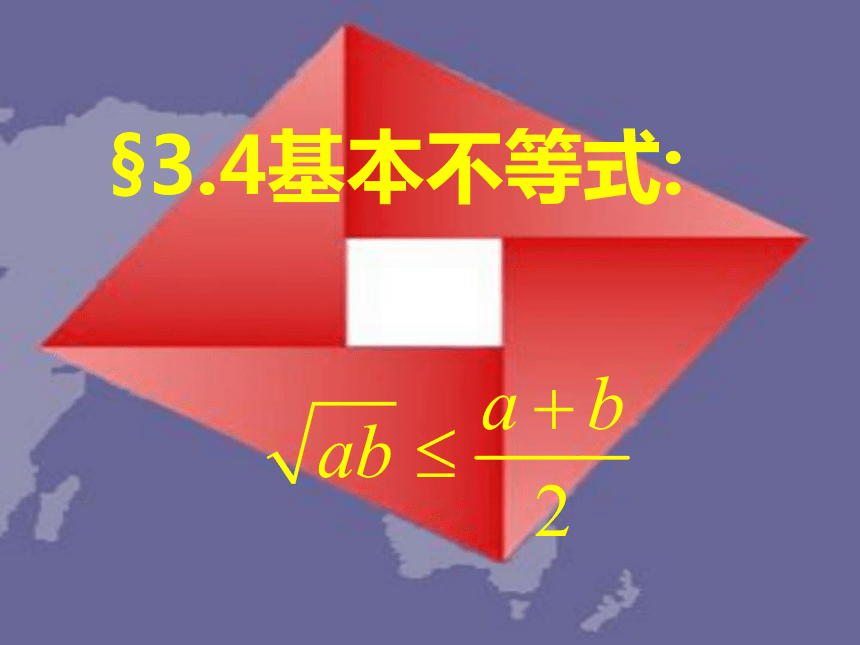
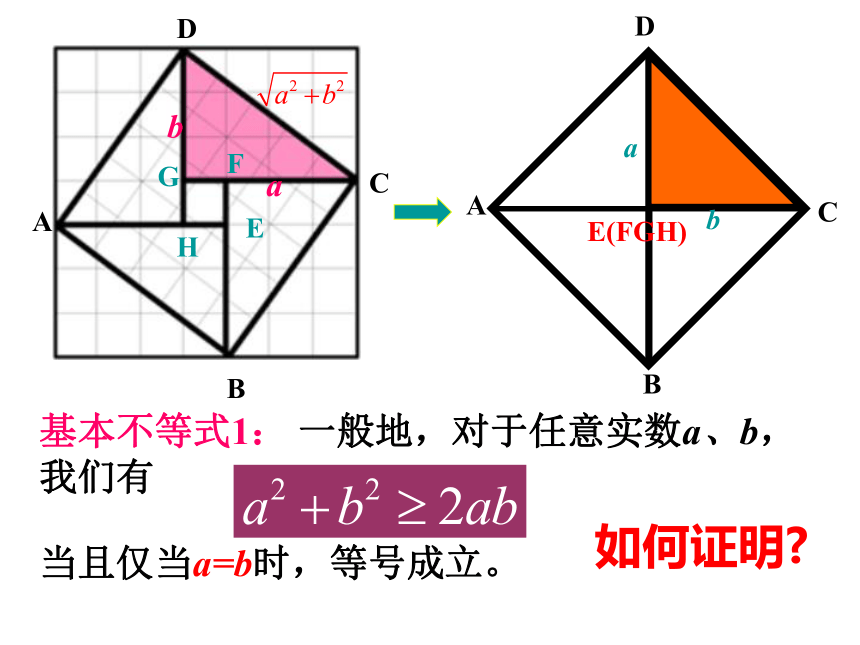
课件20张PPT。§3.4基本不等式:ICM2002会标赵爽:弦图基本不等式1: 一般地,对于任意实数a、b,我们有当且仅当a=b时,等号成立。ABCDE(FGH)ab如何证明?基本不等式2:当且仅当a=b时,等号成立。注意:
(1)两个不等式的适用范围不同,而等号成立的条件相同
(2) 称为正数a、b的几何平均数
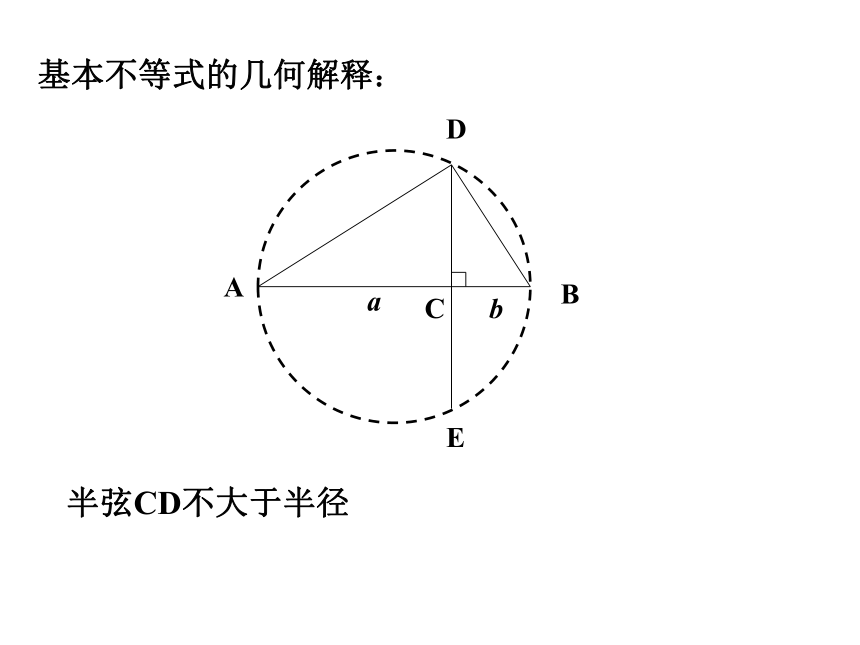
称为它们的算术平均数。如何证明?基本不等式的几何解释:半弦CD不大于半径例1.(1) 已知 并指出等号
成立的条件.(2) 已知 与2的大小关系,
并说明理由.
(3) 已知 能得到什么结论?
请说明理由.
应用一:利用基本不等式判断代数式的大小关系练习2:若
,则( )
(1)(2)(3)B练习1:设a>0,b>0,给出下列不等式其中成立的是
等号能成立的是 。(1)(2)(3)(4)§3.4 基本不等式:应用二:解决最大(小)值问题 例2、已知 都是正数,求证
(1)如果积 是定值P,那么当 时,
和 有最小值
(2)如果和 是定值S,那么当 时,
积 有最大值(1)一正:各项均为正数(2)二定:两个正数积为定值,和有最小值。
两个正数和为定值,积有最大值。(3)三相等:求最值时一定要考虑不等式是否能取“=”,否则会出现错误小结:利用 求最值时要注意下面三条:2、(04重庆)已知
则x y 的最大值是 。1、当x>0时, 的最小值为 ,此时x= 。21 3、若实数 ,且 ,则 的最小
值是( )
A、10 B、 C、 D、D4、在下列函数中,最小值为2的是( )
A、 B、
C、 D、C(4)例3、(1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短篱笆是多少?
(2)一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?例4、某工厂要建造一个长方形无盖贮水池,其容积为4800立方米,深为3米,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?例1、甲、乙两电脑批发商每次在同一电脑耗材厂以相同价格购进电脑芯片。甲、乙两公司共购芯片两次,每次的芯片价格不同,甲公司每次购10000片芯片,乙公司每次购10000元芯片,两次购芯片,哪家公司平均成本低?请给出证明过程。解:设第一、第二次购芯片的价格分别为每片a元和b元例4、 求函数 的最小值构造积为定值,利用基本不等式求最值思考:求函数 的最小值构造和为定值,利用基本不等式求最值例5、已知 ,求 的最大值
)(.34,0,0,0,0.2)(),(1.12222224442cbaabccacbbacbaacadbcbdbcaddcbabayxRyxybxaba++3++3++3+++>>>>+3+?=++证明:求证:已知求证:,是正数,且、已知等式利用基本不等式证明不
(1)两个不等式的适用范围不同,而等号成立的条件相同
(2) 称为正数a、b的几何平均数
称为它们的算术平均数。如何证明?基本不等式的几何解释:半弦CD不大于半径例1.(1) 已知 并指出等号
成立的条件.(2) 已知 与2的大小关系,
并说明理由.
(3) 已知 能得到什么结论?
请说明理由.
应用一:利用基本不等式判断代数式的大小关系练习2:若
,则( )
(1)(2)(3)B练习1:设a>0,b>0,给出下列不等式其中成立的是
等号能成立的是 。(1)(2)(3)(4)§3.4 基本不等式:应用二:解决最大(小)值问题 例2、已知 都是正数,求证
(1)如果积 是定值P,那么当 时,
和 有最小值
(2)如果和 是定值S,那么当 时,
积 有最大值(1)一正:各项均为正数(2)二定:两个正数积为定值,和有最小值。
两个正数和为定值,积有最大值。(3)三相等:求最值时一定要考虑不等式是否能取“=”,否则会出现错误小结:利用 求最值时要注意下面三条:2、(04重庆)已知
则x y 的最大值是 。1、当x>0时, 的最小值为 ,此时x= 。21 3、若实数 ,且 ,则 的最小
值是( )
A、10 B、 C、 D、D4、在下列函数中,最小值为2的是( )
A、 B、
C、 D、C(4)例3、(1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短篱笆是多少?
(2)一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?例4、某工厂要建造一个长方形无盖贮水池,其容积为4800立方米,深为3米,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?例1、甲、乙两电脑批发商每次在同一电脑耗材厂以相同价格购进电脑芯片。甲、乙两公司共购芯片两次,每次的芯片价格不同,甲公司每次购10000片芯片,乙公司每次购10000元芯片,两次购芯片,哪家公司平均成本低?请给出证明过程。解:设第一、第二次购芯片的价格分别为每片a元和b元例4、 求函数 的最小值构造积为定值,利用基本不等式求最值思考:求函数 的最小值构造和为定值,利用基本不等式求最值例5、已知 ,求 的最大值
)(.34,0,0,0,0.2)(),(1.12222224442cbaabccacbbacbaacadbcbdbcaddcbabayxRyxybxaba++3++3++3+++>>>>+3+?=++证明:求证:已知求证:,是正数,且、已知等式利用基本不等式证明不
