19.1.1变量与函数课后练习(含答案)2022-2023学年人教版八年级数学下册
文档属性
| 名称 | 19.1.1变量与函数课后练习(含答案)2022-2023学年人教版八年级数学下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 283.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 21:30:52 | ||
图片预览


文档简介
19.1.1变量与函数课后练习
一、单选题
1.当时,函数的值是( )
A. B. C. D.
2.汽车油箱中有汽油,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:)的增加而减少,平均耗油量为.当时,y与x的函数解析式是( )
A. B. C. D.
3.函数中,自变量的取值范围是( )
A. B. C. D.
4.使函数有意义的自变量x的取值范围为( )
A.x≠0 B.x≥﹣1 C.x≥﹣1且x≠0 D.x>﹣1且x≠0
5.某型号的汽车在路面上的制动距离s=,其中变量是( )
A.s,v B.s,v2 C.s D.v
6.若函数,则当函数值y=8时,自变量x的值是( )
A.± B.4 C.±或4 D.4或-
7.等腰三角形的周长是60cm,腰长(cm)与底边长(cm)的函数解析式正确的是( )
A. B.
C. D.
8.小明骑自行车上学,一开始以某一恒定的速度行驶,但行驶至途中自行车发生了故障,只好停下来修车,车修好后,因怕耽误了上课,他比修车前加快了骑车的速度,下面四幅图中最能反映小明这段行程的是( )
A. B.
C. D.
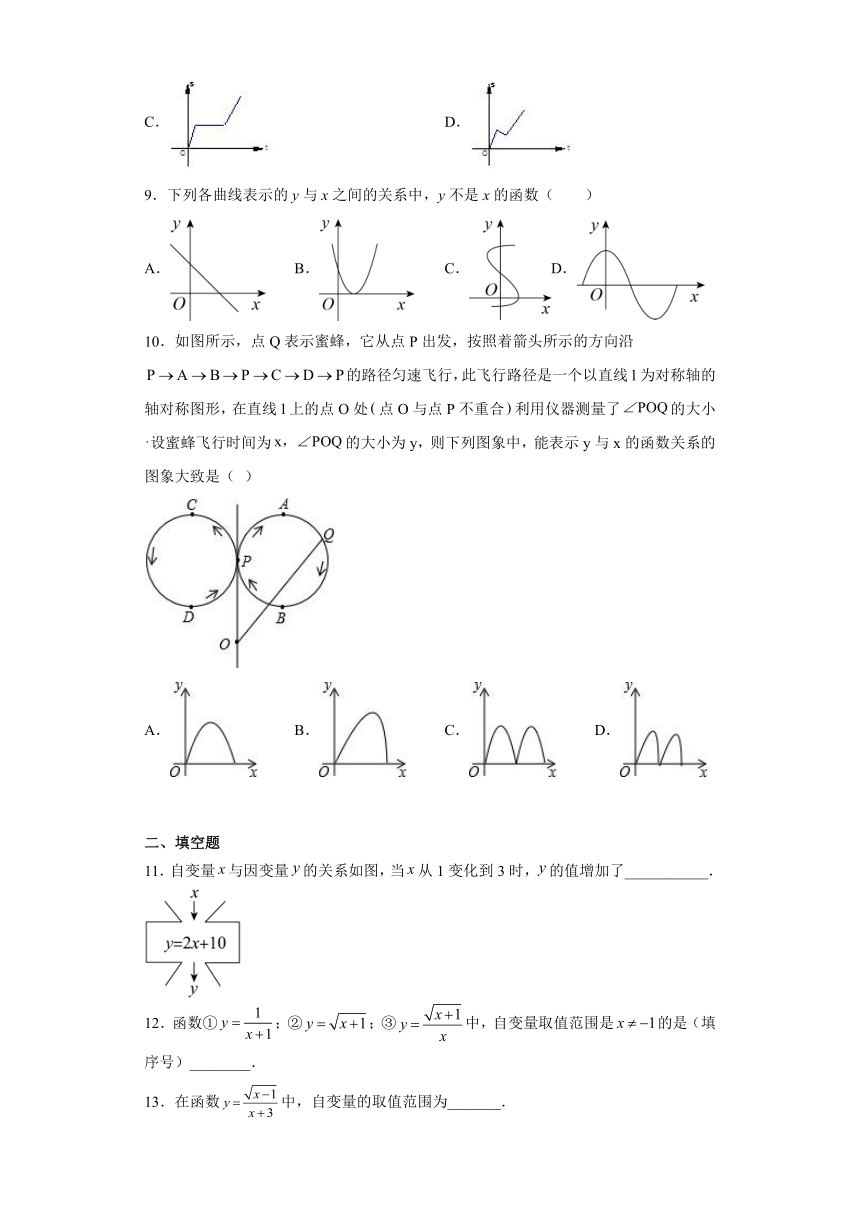
9.下列各曲线表示的y与x之间的关系中,y不是x的函数( )
A. B. C.D.
10.如图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处点O与点P不重合利用仪器测量了的大小设蜜蜂飞行时间为的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
二、填空题
11.自变量与因变量的关系如图,当从1变化到3时,的值增加了___________.
12.函数①;②;③中,自变量取值范围是的是(填序号)________.
13.在函数中,自变量的取值范围为_______.
14.若函数的函数值,则自变量的值为____.
15.请写出一个过点(1,1),且与x轴无交点的函数表达式________________.
三、解答题
16.声音在空气中传播的速度随气温的变化而变化,科学家测得两种气温下声音传播的速度如下表.如果用表示气温,表示该气温下声音在空气中的传播速度,那么,其中,是常数.
气温(℃) 声音的传播速度(米/秒)
0 336
20 342
(1)求,的值;
(2)求气温为时,声音在空气中的传播速度.
17.如图,在一个长为10cm,宽为6cm的长方形的四个角处,都剪去一个大小相等的正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)请写出图中阴影部分的面积与小正方形的边长x(cm)之间的函数关系式;
(2)写出自变量x的取值范围;
(3)当小正方形的边长为2cm时,图中阴影部分的面积为多少?
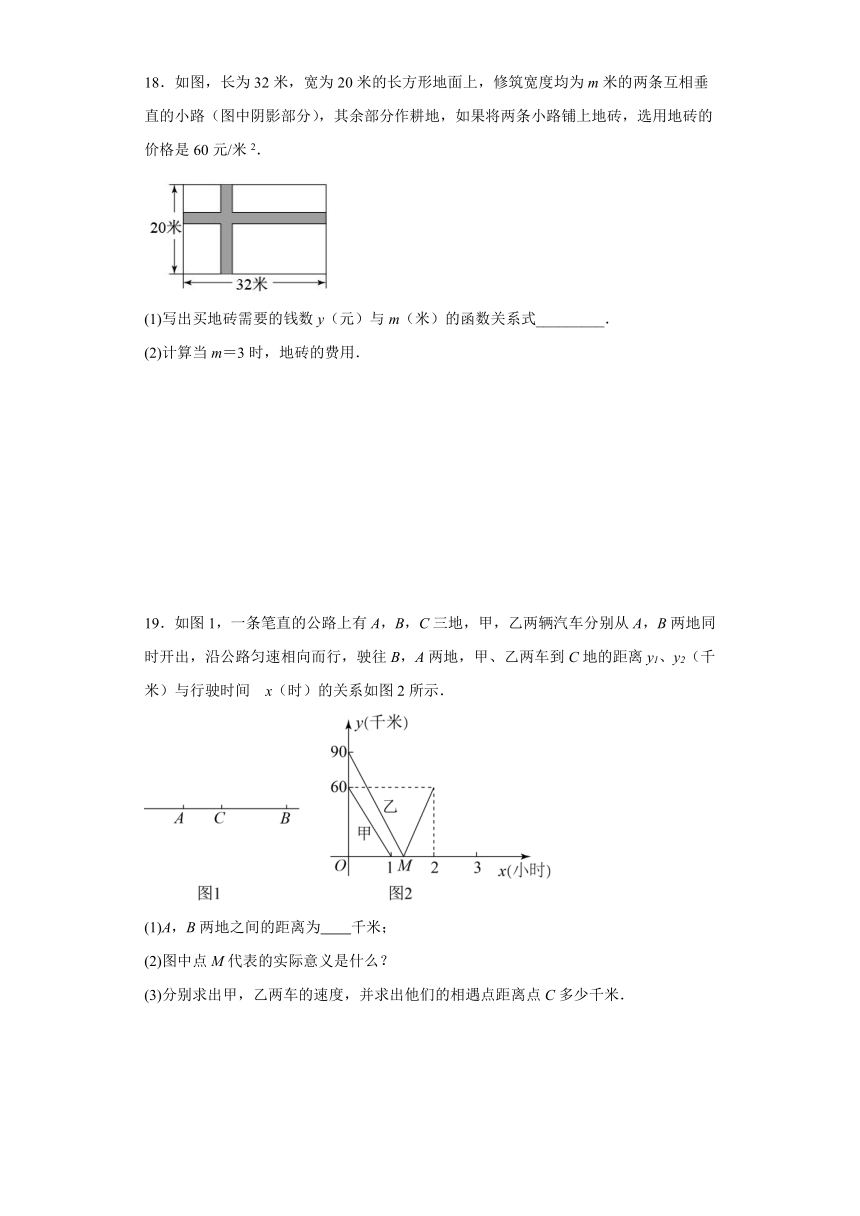
18.如图,长为32米,宽为20米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作耕地,如果将两条小路铺上地砖,选用地砖的价格是60元/米2.
(1)写出买地砖需要的钱数y(元)与m(米)的函数关系式_________.
(2)计算当m=3时,地砖的费用.
19.如图1,一条笔直的公路上有A,B,C三地,甲,乙两辆汽车分别从A,B两地同时开出,沿公路匀速相向而行,驶往B,A两地,甲、乙两车到C地的距离y1、y2(千米)与行驶时间 x(时)的关系如图2所示.
(1)A,B两地之间的距离为 千米;
(2)图中点M代表的实际意义是什么?
(3)分别求出甲,乙两车的速度,并求出他们的相遇点距离点C多少千米.
20.如图1,矩形ABCD中,AB=9,AD=12,点G在CD上,且DG=5,点P从点B出发,以1单位每秒的速度在BC边上向点C运动,设点P的运动时间为x秒.
(1)△APG的面积为y,求y关于x的函数关系式,并求y=34时x的值;
(2)在点P从B向C运动的过程中,是否存在使AP⊥GP的时刻?若存在,求出x的值,若不存在,请说明理由;
(3)如图2,M,N分别是AP、PG的中点,在点P从B向C运动的过程中,线段MN所扫过的图形是什么形状 ,并直接写出它的面积 .
参考答案
1.B
2.B
3.C
4.C
5.A
6.D
7.A
8.C
9.C
10.D
11.4
12.①
13.
14.3或±2
15.答案不唯一,如:
16.(1)将,代入,得,
(2)由(1)知:,将代入得,
气温为时,声音在空气中的传播速度为345米/秒.
17.(1)
即图中阴影部分的面积与小正方形的边长x(cm)之间的函数关系式为:.
(2)自变量x应满足,即
所以自变量x的取值范围为.
(3)当时,
答:图中阴影部分的面积为 .
18.(1)解:根据题意得,
∴ ;
故答案为:;
(2)当时,(元),
∴当时,地砖的费用为8820元.
19.(1)解:由图象可知AC=60,BC=90,
∴A、B两地距离为60+90=150km;
∴A、B两地距离为150千米;
故答案为:150.
(2)解:由图象可知,点M代表的实际意义是:乙到达C的时间.
(3)解:由图象可知:甲乙两车匀速运动,AC=60,BC=90,
∴甲车的速度:60÷1=60(千米/小时),
乙车的速度为:150÷2= 75(千米/小时),
设经过x小时甲乙两车相遇,根据题意列方程,得
(60+75)x=150
解得x=;
由图像知已到达C的距离为90千米,那么
他们的相遇点与点C的距离为:90-75×=(千米).
∴他们的相遇点与点C的距离为千米.
20.解:(1)∵四边形ABCD为矩形,
∴DC=AB=9,AD=BC=12.
∵DG=5,
∴GC=4.
∵PB=x,PC=12-x,
∴y=9×12-×9×x-×4×(12-x)-×5×12,整理得:y=-2.5x+54.
当y=34时,-2.5x+54=34,解得x=8;
(2)存在.
∵PB=x,PC=12-x,AD=12,DG=5,
∴PA2=AB2+BP2=81+x2,PG2=PC2+GC2=(12-x)2+16,AG2=AD2+DG2=169.
∵当AG2=AP2+PG2时,AP⊥PG,
∴81+x2+(12-x)2+16=169,整理得:x2-12x+36=0,配方得:(x-6)2=0,
解得:x=6;
(3)如图所示:
∵当点P与点B重合时,点M位于M1处,点N位于点N1处,
∴M1为AB的中点,点N1位GB的中点.
∵当点P与点C重合时,点M位于M2处,点N位于点N2处,
∴M2为AC的中点,点N2位CG的中点.
∴M1M2∥BC,M1M2=BC,N1N2∥BC,N1N2=BC.
∴M1M2∥N1N2,N1N2=M1M2.
∴四边形M1M2N2N1为平行四边形.
∴MN扫过的区域为平行四边形.
S=BC (AB-CG)=6×2.5=15,
故答案为:平行四边形;15.
一、单选题
1.当时,函数的值是( )
A. B. C. D.
2.汽车油箱中有汽油,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:)的增加而减少,平均耗油量为.当时,y与x的函数解析式是( )
A. B. C. D.
3.函数中,自变量的取值范围是( )
A. B. C. D.
4.使函数有意义的自变量x的取值范围为( )
A.x≠0 B.x≥﹣1 C.x≥﹣1且x≠0 D.x>﹣1且x≠0
5.某型号的汽车在路面上的制动距离s=,其中变量是( )
A.s,v B.s,v2 C.s D.v
6.若函数,则当函数值y=8时,自变量x的值是( )
A.± B.4 C.±或4 D.4或-
7.等腰三角形的周长是60cm,腰长(cm)与底边长(cm)的函数解析式正确的是( )
A. B.
C. D.
8.小明骑自行车上学,一开始以某一恒定的速度行驶,但行驶至途中自行车发生了故障,只好停下来修车,车修好后,因怕耽误了上课,他比修车前加快了骑车的速度,下面四幅图中最能反映小明这段行程的是( )
A. B.
C. D.
9.下列各曲线表示的y与x之间的关系中,y不是x的函数( )
A. B. C.D.
10.如图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处点O与点P不重合利用仪器测量了的大小设蜜蜂飞行时间为的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
二、填空题
11.自变量与因变量的关系如图,当从1变化到3时,的值增加了___________.
12.函数①;②;③中,自变量取值范围是的是(填序号)________.
13.在函数中,自变量的取值范围为_______.
14.若函数的函数值,则自变量的值为____.
15.请写出一个过点(1,1),且与x轴无交点的函数表达式________________.
三、解答题
16.声音在空气中传播的速度随气温的变化而变化,科学家测得两种气温下声音传播的速度如下表.如果用表示气温,表示该气温下声音在空气中的传播速度,那么,其中,是常数.
气温(℃) 声音的传播速度(米/秒)
0 336
20 342
(1)求,的值;
(2)求气温为时,声音在空气中的传播速度.
17.如图,在一个长为10cm,宽为6cm的长方形的四个角处,都剪去一个大小相等的正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)请写出图中阴影部分的面积与小正方形的边长x(cm)之间的函数关系式;
(2)写出自变量x的取值范围;
(3)当小正方形的边长为2cm时,图中阴影部分的面积为多少?
18.如图,长为32米,宽为20米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作耕地,如果将两条小路铺上地砖,选用地砖的价格是60元/米2.
(1)写出买地砖需要的钱数y(元)与m(米)的函数关系式_________.
(2)计算当m=3时,地砖的费用.
19.如图1,一条笔直的公路上有A,B,C三地,甲,乙两辆汽车分别从A,B两地同时开出,沿公路匀速相向而行,驶往B,A两地,甲、乙两车到C地的距离y1、y2(千米)与行驶时间 x(时)的关系如图2所示.
(1)A,B两地之间的距离为 千米;
(2)图中点M代表的实际意义是什么?
(3)分别求出甲,乙两车的速度,并求出他们的相遇点距离点C多少千米.
20.如图1,矩形ABCD中,AB=9,AD=12,点G在CD上,且DG=5,点P从点B出发,以1单位每秒的速度在BC边上向点C运动,设点P的运动时间为x秒.
(1)△APG的面积为y,求y关于x的函数关系式,并求y=34时x的值;
(2)在点P从B向C运动的过程中,是否存在使AP⊥GP的时刻?若存在,求出x的值,若不存在,请说明理由;
(3)如图2,M,N分别是AP、PG的中点,在点P从B向C运动的过程中,线段MN所扫过的图形是什么形状 ,并直接写出它的面积 .
参考答案
1.B
2.B
3.C
4.C
5.A
6.D
7.A
8.C
9.C
10.D
11.4
12.①
13.
14.3或±2
15.答案不唯一,如:
16.(1)将,代入,得,
(2)由(1)知:,将代入得,
气温为时,声音在空气中的传播速度为345米/秒.
17.(1)
即图中阴影部分的面积与小正方形的边长x(cm)之间的函数关系式为:.
(2)自变量x应满足,即
所以自变量x的取值范围为.
(3)当时,
答:图中阴影部分的面积为 .
18.(1)解:根据题意得,
∴ ;
故答案为:;
(2)当时,(元),
∴当时,地砖的费用为8820元.
19.(1)解:由图象可知AC=60,BC=90,
∴A、B两地距离为60+90=150km;
∴A、B两地距离为150千米;
故答案为:150.
(2)解:由图象可知,点M代表的实际意义是:乙到达C的时间.
(3)解:由图象可知:甲乙两车匀速运动,AC=60,BC=90,
∴甲车的速度:60÷1=60(千米/小时),
乙车的速度为:150÷2= 75(千米/小时),
设经过x小时甲乙两车相遇,根据题意列方程,得
(60+75)x=150
解得x=;
由图像知已到达C的距离为90千米,那么
他们的相遇点与点C的距离为:90-75×=(千米).
∴他们的相遇点与点C的距离为千米.
20.解:(1)∵四边形ABCD为矩形,
∴DC=AB=9,AD=BC=12.
∵DG=5,
∴GC=4.
∵PB=x,PC=12-x,
∴y=9×12-×9×x-×4×(12-x)-×5×12,整理得:y=-2.5x+54.
当y=34时,-2.5x+54=34,解得x=8;
(2)存在.
∵PB=x,PC=12-x,AD=12,DG=5,
∴PA2=AB2+BP2=81+x2,PG2=PC2+GC2=(12-x)2+16,AG2=AD2+DG2=169.
∵当AG2=AP2+PG2时,AP⊥PG,
∴81+x2+(12-x)2+16=169,整理得:x2-12x+36=0,配方得:(x-6)2=0,
解得:x=6;
(3)如图所示:
∵当点P与点B重合时,点M位于M1处,点N位于点N1处,
∴M1为AB的中点,点N1位GB的中点.
∵当点P与点C重合时,点M位于M2处,点N位于点N2处,
∴M2为AC的中点,点N2位CG的中点.
∴M1M2∥BC,M1M2=BC,N1N2∥BC,N1N2=BC.
∴M1M2∥N1N2,N1N2=M1M2.
∴四边形M1M2N2N1为平行四边形.
∴MN扫过的区域为平行四边形.
S=BC (AB-CG)=6×2.5=15,
故答案为:平行四边形;15.
