高中数学北师大版(2019)必修第二册4.3.1二倍角公式(教学课件)-(共107张)
文档属性
| 名称 | 高中数学北师大版(2019)必修第二册4.3.1二倍角公式(教学课件)-(共107张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 00:00:00 | ||
图片预览










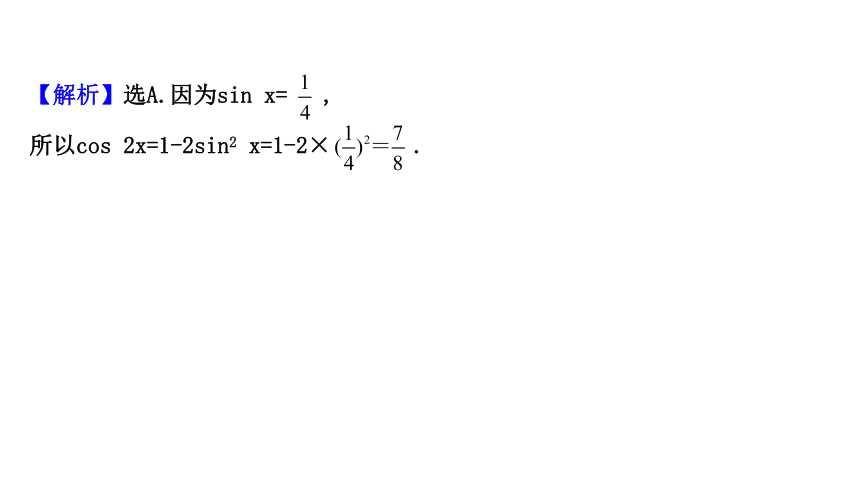

文档简介
(共107张PPT)
§3 二倍角的三角函数公式
3.1 二倍角公式
必备知识·自主学习
1.倍角公式
(1)sin 2α= ______________(S2α).
(2)cos 2α= _____________
= _________=1-2sin2α(C2α).
(3)tan 2α=___________(T2α).
导思 1.如何根据两角和差的正弦、余弦及正切公式推出二倍角公式
2.二倍角公式有哪些变形式
2sin αcos α
cos2α-sin2α
2cos2α-1
【思考】
(1)所谓的“倍角”公式,就是角α与2α之间的转化关系,对吗
提示:不对.对于“倍角”应该广义地理解,如:8α是4α的二倍角,3α是 α
的倍角,α是 的倍角, 是 的倍角,…,这里蕴含着换元思想.这就是说
“倍”是相对而言的,是描述两个数量之间关系的.
(2)公式中的角α是任意角吗
提示:对于公式S2α,C2α中的角α是任意角,但是T2α中的角α要保证tan α有意义且分母1-tan2α≠0.
即α≠kπ+ 且α≠kπ+ ,k∈Z.
2.倍角公式的变换
(1)因式分解变换
cos 2α=cos2α-sin2α=(cos α+sin α)(cos α-sin α).
(2)配方变换
1±sin 2α=sin2α+cos2α±2sin αcos α=(sin α±cos α)2.
(3)升幂缩角变换
1+cos 2α=2cos2α,1-cos 2α=2sin2α.
(4)降幂扩角变换
cos2α= (1+cos 2α),sin2α= (1-cos 2α),
sinαcos α= sin 2α.
【思考】
以上公式的变换可以在做题中直接运用吗
提示:可以,尤其是上面(4)应用的频率非常高.
【基础小测】
1.辨析记忆(对的打“√”,错的打“×”)
(1)倍角的正切公式的适用范围不是任意角. ( )
(2)对于任意的角α,都有sin 2α=2sin α成立. ( )
(3)存在角α,使cos 2α=2cos α成立. ( )
(4)cos 3αsin 3α= sin 6α对任意的角α都成立. ( )
提示:(1)√.倍角的正切公式,要求α≠ +kπ(k∈Z)且α≠± +kπ(k∈Z),故此说法正确.
(2)×.当α= 时,sin 2α=sin ,而2sin α=2× =1.
(3)√.由cos 2α=2cos α=2cos2α-1,得cos α= 时,cos 2α=2cos α
成立.
(4)√.由倍角的正弦公式可得.
2.已知sin x= ,则cos 2x的值为 ( )
【解析】选A.因为sin x= ,
所以cos 2x=1-2sin2 x=1-2× .
3.(教材二次开发:例题改编)若tan 2α=2,则tan 4α=________.
【解析】tan 4α= .
答案:-
关键能力·合作学习
类型一 倍角公式的求值问题(数学运算)
【题组训练】
1.sin 10°sin 30°sin 50°sin 70°=________.
2.计算: =________.
3.已知cos ,α∈ ,则 =________.
【解析】1.原式=cos 80°cos 60°cos 40°cos 20°=
答案:
2.原式= .
答案:2
3.
=2cos =2sin ,
因为0<α< ,所以0< -α< ,
又 ,所以 ,
所以原式=2× .
答案:
【解题策略】
1.倍角公式正用、逆用解题的关注点
(1)注意观察式子的结构特点及角之间是否存在特殊的倍数关系,灵活正用或逆用倍角公式.
(2)结合诱导公式恰当变化函数名称,灵活处理系数,构造倍角公式的形式.
2.条件求值问题的解题实质
条件求值问题的解题实质是对已知条件与要求问题进行化简变形,最终代入已知条件求值;其解题突破口为已知条件与要求问题中角的特点,解题关键在于“变角”,即把“所求角”变为“已知角”.
【补偿训练】
(2020·沈阳高一检测)已知sin =
3cos(2π+α),其中α为锐角,
(1)求10sin2 的值;
(2)求 ·tan 2α的值.
【解析】化简sin =3cos(2π+α)得sin α=
3cos α,又因为sin2α+cos2α=1且α为锐角,
所以可得cos α= ,sin α= .
且由sin α=3cos α可得tan α=3.
(1)10sin2
=10sin2α- cos α-tan α
=10× -3=5.
(2)因为tan 2α= ;
cos 2α-sin 2α=cos2α-sin2α-2sin αcos α
,
所以 .
类型二 倍角公式的化简、证明问题(数学运算、逻辑推理) 角度1 化简问题
【典例】化简 =________.
【思路导引】结合二倍角公式化简求解.
【解析】原式=
=2|cos 4|-2|sin 4+cos 4|,
因为π<4< ,
所以cos 4<0,sin 4+cos 4<0.
所以原式=-2cos 4+2(sin 4+cos 4)=2sin 4.
答案:2sin 4
【变式探究】
化简 ,其中θ∈(0,π).
【解析】
原式=
①当θ∈ 时, ,
此时原式=sin +cos -cos +sin =2sin .
②当θ∈ 时, ∈ ,cos此时原式=sin +cos -sin +cos =2cos .
角度2 恒等式证明问题
【典例】求证:cos2(A+B)-sin2(A-B)=cos 2Acos 2B.
【思路导引】可考虑从左向右证的思路:先把左边降幂扩角,再用余弦的和、差角公式转化为右边形式.
【证明】左边=
=
= (cos 2Acos 2B-sin 2Asin 2B+cos 2Acos 2B+
sin 2Asin 2B)=cos 2Acos 2B=右边,
所以等式成立.
【解题策略】
1.三角函数式的化简原则
三角函数式的化简原则:一是统一角,二是统一函数名.能求值的求值,必要时切化弦,更易通分、约分.
2.证明三角恒等式的原则与步骤
(1)观察恒等式两端的结构形式,处理原则是从复杂到简单,高次降低,复角化单角,如果两端都比较复杂,就将两端都化简,即采用“两头凑”的思想.
(2)证明恒等式的一般步骤
①先观察,找出角、函数名称、式子结构等方面的差异;
②本着“复角化单角”“异名化同名”“变换式子结构”“变量集中”等原则,设法消除差异,达到证明的目的.
【题组训练】
1.cos4 -sin4 的化简结果为 ( )
A.cos B.cos α C.cos 2α D.cos 4α
【解析】选B.cos4 -sin4
= =cos α.
2.化简: .
【解析】原式=
= =2.
3.求证: cos2θ(1-tan2θ)=cos 2θ.
【证明】方法一:左边=cos2θ
=cos2θ-sin2θ=cos 2θ=右边.故原式得证.
方法二:右边=cos 2θ=cos2θ-sin2θ
=cos2θ =cos2θ(1-tan2θ)=左边.故原式得证.
【补偿训练】
求证:
=tan .
【证明】左边=
=
=
= =右边,故原式得证.
类型三 倍角公式与三角函数性质的综合问题(逻辑推理)
【典例】已知函数f(x)=sin2x-sin2 ,x∈R.
(1)求f(x)的最小正周期.
(2)求f(x)在区间 上的最大值和最小值.
【解题策略】
倍角公式与三角函数性质的综合问题的解题策略
运用三角函数的和、差、倍角公式将函数关系式化成y=asin ωx+bcos ωx+k的形式,借助辅助角公式化为y=
Asin(ωx+φ)+k(或y=Acos(ωx+φ)+k)的形式,将ωx+φ看作一个整体研究函数的性质.
【跟踪训练】
已知函数f(x)=2 sin xcos x-2cos2x+1(x∈R).
(1)求函数f(x)的最小正周期及在区间 上的最大值和最小值.
(2)若f(x0)= ,x0∈ ,求cos 2x0的值.
【解析】(1)由f(x)=2 sin xcos x-2cos2x+1,
得f(x)= (2sin xcos x)-(2cos2x-1)
= sin 2x-cos 2x=2sin ,
所以函数f(x)的最小正周期为π.
易知f(x)=2sin 在区间 上为增函数,
在区间 上为减函数,
又f(0)=-1,f =2,f =-1,所以函数f(x)在 上的最大值为2,
最小值为-1.
(2)因为2sin ,所以sin .
又x0∈ ,所以2x0- ∈ ,
所以cos .
所以cos 2x0=cos
=cos
= .
【拓展延伸】
倍角公式的广义理解
对于二倍角公式有广义上的理解.如8α是4α的二倍角;6α是3α的二倍角;3α
是 α的二倍角; α是 α的二倍角;…….又如:α=2· ,
=2· ,…, =2· (n∈N*),
所以sin =2sin cos (n∈N*),
cos =cos2 -sin2 (n∈N*),
tan = (n∈N*).一般情况下,sin 2α≠2sin α,
只有当α=nπ(n∈Z)时,sin 2α=2sin α才成立,同样的cos 2α=2cos α,
tan 2α=2tan α在一般
情况下也不成立.
【拓展训练】
(2020·扬州高一检测)已知sin α+cos α= ,则sin 2α+cos 4α的
值为________.
【思路导引】先平方求出sin 2α,再利用二倍角公式求出cos 4α,即可求解.
【解析】因为sin α+cos α= ,
所以 =1+sin 2α= ,
即sin 2α=- ,
cos 4α=1-2sin22α=1-2× ,
sin 2α+cos 4α=- .
答案:
1.(2020·杭州高一检测)已知cos x= ,则cos 2x= ( )
【解析】选D.由cos x= 得cos 2x=2cos2x-1=2× -1= .
课堂检测·素养达标
2.若 ,则tan 2α等于 ( )
【解析】选B.因为 ,
所以 ,故tan α=-3,
所以根据倍角公式,得tan 2α= .
3.(教材二次开发:练习改编)(多选题)(2020·福州高一检测)若sin α>sin β
>0,则下列不等式中不一定成立的是 ( )
A.sin 2α>sin 2β B.cos 2αC.cos 2α>cos 2β D.sin 2α【解析】选AD.因为cos 2α=1-2sin2α,
cos 2β=1-2sin2β,
因为sin α>sin β>0,
所以sin2α>sin2β>0,-2sin2α<-2sin2β,
则1-2sin2α<1-2sin2β,
即cos 2α则B一定成立,C一定不成立;
当α= ,β= 时,
sin α>sin β>0,sin 2α=1> =sin 2β,
当α= ,β= 时,sin α>sin β>0,sin 2α=0< =sin 2β,
则AD可能成立,也可能不成立.
4.函数f(x)=sin -2 ·sin2x的最小正周期是________.
【解析】f(x)=sin -2 sin2x
= sin 2x- cos 2x-2 ×
= sin 2x+ cos 2x-
=sin ,
故最小正周期为π.
答案:π
5.(2020·铜川高一检测)已知cos β= ,sin(α-β)= ,且0<β<α< .
(1)求tan 2β的值;(2)求sin α的值.
【解析】(1)由cos β= ,0<β< ,得sin β=
则tan 2β= .
(2)由0<β<α< ,得0<α-β< ,
所以cos(α-β)= .
sin α=sin[(α-β)+β]
=sin(α-β)cos β+cos(α-β)sin β
= .
三十三 二倍角公式
【基础通关——水平一】 (15分钟 35分)
1.(2020·成都高一检测)设单位向量e= ,则cos 2α的值为 ( )
【解析】选A.由题设可得cos2α+ =1 cos2α= ,则cos 2α=2cos2α-
1= .
课时素养评价
2.已知sin 2θ=- ,则tan θ+ = ( )
【解析】选D.因为sin 2θ=2sin θcos θ=- ,
所以sin θcos θ=- ,
所以tan θ+ .
【补偿训练】
设sin α= ,tan(π-β)= ,则tan(α-2β)=( )
【解析】选D.因为sin α= ,α∈ ,
所以cos α=- ,所以tan α=- .
又tan(π-β)= ,所以tan β=- ,
所以tan 2β= .
所以tan(α-2β)= .
3.(2020·大理高一检测)已知角α+ 的终边与单位圆x2+y2=1交于P ,
则sin 2α等于 ( )
【解析】选A.由任意角三角函数定义可得sin ,则sin 2α=
-cos =2sin2 -1=- .
4.已知tan α= ,则cos2α+sin 2α的结果为________.
【解析】因为tan α= ,所以 ,
即2sin α=cos α,
所以sin2α+cos2α= cos2α+cos2α=1,
即cos2α= ,所以cos2α+sin 2α=cos2α+2sin α·cos α=2cos2α= .
答案:
5.(2020·广州高一检测)若sin ,则
cos =________.
【解析】已知sin ,且 ,则cos =
sin ,故cos =2cos2 -1=- .
答案:-
6.(2020·宁波高一检测)已知函数f(x)=
2sin x( cos x+sin x)-1.
(1)求f(x)的单调递增区间;
(2)若f ,求sin 的值.
【解析】(1)f(x)=2 sin xcos x+2sin2x-1= sin 2x-cos 2x=2sin ,
令- +2kπ≤2x- ≤ +2kπ,k∈Z,解得- +kπ≤x≤ +kπ,
k∈Z,
故单调递增区间为 (k∈Z).
(2)由f 得sin ,
则sin =sin =cos =1-2sin2 .
【能力进阶——水平二】 (30分钟 60分)
一、单选题(每小题5分,共20分)
1.若sin α+cos α= ,0<α<π,则sin 2α+cos 2α= ( )
【解析】选A.因为sin α+cos α= ,①
所以1+2sin αcos α= ,
即2sin αcos α=sin 2α=- ,
所以1-2sin αcos α=(sin α-cos α)2= .
因为sin αcos α<0,且0<α<π,
所以sin α>0,cos α<0,
所以sin α-cos α= .②
①×②变形得cos2α-sin2α=cos 2α=- ,
所以sin 2α+cos 2α=- .
2.(2020·全国Ⅰ卷)已知α∈(0,π),且3cos 2α-8cos α=5,则sin α= ( )
【解析】选A.由3cos 2α-8cos α=5,
得6cos2α-8cos α-8=0,
即3cos2α-4cos α-4=0,
解得cos α=- 或cos α=2(舍去),
又因为α∈(0,π),所以sin α= .
【补偿训练】
(2020·合肥高一检测)若cos ,则cos = ( )
【解析】选C.cos =cos
=cos =cos
=2cos2 -1=2× -1=- .
3.(2020·石家庄高一检测)若角α∈ ,β∈ , sin β=cos -sin ,sin α= ,则cos β= ( )
【解析】选A.由题意可得sin β=sin .
因为 ∈ ,β∈ ,
所以 =β,则2β= -α,
所以cos 2β=cos =sin α= ,
又cos 2β=2cos2β-1= ,解得cos2β= ,
又β∈ ,所以cos β= .
4.(2020·合肥高一检测)已知函数f(x)=sin(x+φ+θ)的图象关于直线x=π对称,其中0<φ<π,- <θ<0,且tan θ=-2,则sin 2φ的值为 ( )
【解析】选D.因为函数f(x)=sin(x+φ+θ)的图象关于直线x=π对称,所以由正弦函数的图象与性质可知π+φ+θ= +kπ,k∈Z,
则θ=- -φ+kπ,k∈Z,
所以tan θ= =-2,
即tan =2,故 =2,化简得cos φ=-2sin φ,又sin2φ+cos2φ=1 ,
解得sin2φ= ,
因为0<φ<π,所以sin φ>0,则sin φ= ,而由cos φ=-2sin φ,可得cos φ
= ,
所以sin 2φ=2sin φcos φ=2× × =- .
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错
的得0分)
5.(2020·盐城高一检测)下列各式中,值为 的是 ( )
A.sin 15°cos 15° B.cos2 -sin2
C. D.
【解析】选CD.因为sin 15°cos 15°= sin 30°
= × = ,所以A不正确;
因为cos2 -sin2
=cos ,所以B不正确;
因为 ,所以C正确;
因为 ,所以D正确.
6.在△ABC中,若acos A=bcos B,则△ABC的形状可能为 ( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
【解析】选ABCD.根据正弦定理 ,
因为 acos A=bcos B,
所以sin Acos A=sin Bcos B,
即sin 2A=sin 2B.
因为2A,2B∈(0,2π),
所以2A=2B或2A+2B=π,即A=B或A+B= ,
所以△ABC可能为:直角三角形,等腰三角形,等腰直角三角形,等边三角形.
三、填空题(每小题5分,共10分)
7.函数y=sin xcos x+ cos2x- 的图象的一个对称中心为________.
【解析】y= sin 2x+ (1+cos 2x)-
= sin 2x+ cos 2x- =sin - ,
令2x+ =kπ,x= (k∈Z),
当k=1时,x= ,对称中心是 ;
当k=2时,x= ,对称中心是 .
答案: (答案不唯一)
【补偿训练】
已知函数f(x)= cos2x-sin xcos x- ,则f =________;函数f(x)
在 上的值域为________.
【解析】由题可知f(x)= cos2x-sin xcos x- ,
则f(x)=
= cos 2x- sin 2x,
所以f(x)=cos ,
则f =cos =0,
因为x∈ ,所以2x+ ∈ ,
又函数y=cos t在 上单调递减,在 上单调递增,当2x+ =π,
即x= 时,f(x)min=cos π=-1.
当2x+ = ,
即x=0时,f(x)max=cos = .
所以函数f(x)在 上的值域为 .
答案:0
8.已知cos ,=________.
【解析】
=
=sin 2x·tan ,
因为又因为cos ,
所以sin .
所以tan .
所以cos x=cos
=cos cos +sin sin = .
sin x=sin
=sin cos -sin cos
= ,
可得sin 2x=2sin xcos x=2× .
所以 .
答案:
四、解答题(每小题10分,共20分)
9.已知sin -2cos =0.
求 的值.
【解析】由sin -2cos =0,知cos ≠0,
所以tan =2,
所以tan x= .
所以
= =
=
= .
10.(2020·扬州高一检测)从秦朝统一币制到清朝末年,圆形方孔铜钱(简称“孔方兄”)是我国使用时间长达两千多年的货币.如图1,这是一枚清朝同治年间的铜钱,其边框是由大小不等的两同心圆围成的,内嵌正方形孔的中心与同心圆圆心重合,正方形外部,圆框内部刻有四个字“同治重宝”.某模具厂计划仿制这样的铜钱作为纪念品,其小圆内部图纸设计如图2所示,小圆直径1厘米,内嵌一个大正方形孔,四周是四个全等的小正方形(边长比孔的边长小),每个正方形有两个顶点在圆周上,另两个顶点在孔边上,四个小正方形内用于刻铜钱上的字.设∠OAB=θ,五个正方形的面积和为S.
(1)求面积S关于θ的函数表达式,并求定义域;
(2)求面积S的最小值及此时tan θ的值.
【解析】(1)过点O分别作小正方形边、大正方形边的垂线,垂足分别为E,F,
因为内嵌一个大正方形孔的中心与同心圆圆心重合,所以点E,F分别为小正方
形和大正方形边的中点,所以小正方形的边长为 ×2=sin θ,大正方形
的边长为 ×2=cos θ-2sin θ,
所以五个正方形的面积和为S=4sin2θ+
=8sin2θ+cos2θ-4sin θcos θ,
因为小正方形边长小于内嵌一个大正方形的边长,
所以sin θ所以θ的取值范围为 ,
所以面积S关于θ的函数表达式为S=8sin2θ+cos2θ-4sin θcos θ,
θ的取值范围为 ,tanθ0= ,θ0∈ .
(2)方法一:S=8sin2θ+cos2θ-4sin θcos θ
=8× -2sin 2θ
=
= ,其中tan φ= ,φ∈ ,
所以Smin= ,此时sin =1,因为θ∈ ,
所以0<2θ+φ<2θ0+ < π,
所以2θ+φ= ,
所以tan 2θ=tan ,
则tan 2θ= ,
化简得:2tan2θ+7tan θ-2=0,由此解得tan θ= ,
因为0所以tan θ= .
故面积S最小值为 ,此时tan θ= .
【创新迁移】
1.(2020·合肥高一检测)1626年,阿贝尔特格洛德最早推出简写的三角符
号:sin,tan,sec(正割),1675年,英国人奥屈特最早推出余下的简写三角符
号:cos,cot,csc(余割),但直到1748年,经过数学家欧拉的引用后,才逐渐通用
起来,其中secθ= ,csc θ= .若α∈(0,π),且 =2,则
tan α= ( )
【解析】选D.因为3sin α+2cos α=2,
所以 =2,
所以 =2,
所以3tan +1-tan2 =tan2 +1,解得tan =0或 .
又因为α∈(0,π),
所以tan >0,
所以tan = ,
则tan α= .
2.在△ABC中,设向量m=(sin A,cos B),n=(sin B,cos A)且m∥n,m≠n.
(1)求证:A+B= .
(2)求sin A+sin B的取值范围.
(3)若(sin Asin B)x=sin A+sin B,试确定实数x的取值范围.
【解析】(1)因为向量m=(sin A,cos B),n=(sin B,cos A)且m∥n,
所以sin Acos A-sin Bcos B=0,即sin 2A=sin 2B,解得2A=2B或2A+2B=π,
化简可得A=B,或A+B= ,但A=B时有m=n,与已知矛盾,故舍去,故有A+B= .
(2)由(1)可知A+B= ,故sin A+sin B
=sin A+sin =sin A+cos A
= sin ,
因为0所以1< sin ≤ ,故sin A+sin B的取值范围是(1, ].
(3)由题意可知x= ,
设sin A+cos A=t∈(1, ],则t2=1+2sin Acos A,
故sin Acos A= ,代入得x= ,
故实数x的取值范围为[2 ,+∞).
§3 二倍角的三角函数公式
3.1 二倍角公式
必备知识·自主学习
1.倍角公式
(1)sin 2α= ______________(S2α).
(2)cos 2α= _____________
= _________=1-2sin2α(C2α).
(3)tan 2α=___________(T2α).
导思 1.如何根据两角和差的正弦、余弦及正切公式推出二倍角公式
2.二倍角公式有哪些变形式
2sin αcos α
cos2α-sin2α
2cos2α-1
【思考】
(1)所谓的“倍角”公式,就是角α与2α之间的转化关系,对吗
提示:不对.对于“倍角”应该广义地理解,如:8α是4α的二倍角,3α是 α
的倍角,α是 的倍角, 是 的倍角,…,这里蕴含着换元思想.这就是说
“倍”是相对而言的,是描述两个数量之间关系的.
(2)公式中的角α是任意角吗
提示:对于公式S2α,C2α中的角α是任意角,但是T2α中的角α要保证tan α有意义且分母1-tan2α≠0.
即α≠kπ+ 且α≠kπ+ ,k∈Z.
2.倍角公式的变换
(1)因式分解变换
cos 2α=cos2α-sin2α=(cos α+sin α)(cos α-sin α).
(2)配方变换
1±sin 2α=sin2α+cos2α±2sin αcos α=(sin α±cos α)2.
(3)升幂缩角变换
1+cos 2α=2cos2α,1-cos 2α=2sin2α.
(4)降幂扩角变换
cos2α= (1+cos 2α),sin2α= (1-cos 2α),
sinαcos α= sin 2α.
【思考】
以上公式的变换可以在做题中直接运用吗
提示:可以,尤其是上面(4)应用的频率非常高.
【基础小测】
1.辨析记忆(对的打“√”,错的打“×”)
(1)倍角的正切公式的适用范围不是任意角. ( )
(2)对于任意的角α,都有sin 2α=2sin α成立. ( )
(3)存在角α,使cos 2α=2cos α成立. ( )
(4)cos 3αsin 3α= sin 6α对任意的角α都成立. ( )
提示:(1)√.倍角的正切公式,要求α≠ +kπ(k∈Z)且α≠± +kπ(k∈Z),故此说法正确.
(2)×.当α= 时,sin 2α=sin ,而2sin α=2× =1.
(3)√.由cos 2α=2cos α=2cos2α-1,得cos α= 时,cos 2α=2cos α
成立.
(4)√.由倍角的正弦公式可得.
2.已知sin x= ,则cos 2x的值为 ( )
【解析】选A.因为sin x= ,
所以cos 2x=1-2sin2 x=1-2× .
3.(教材二次开发:例题改编)若tan 2α=2,则tan 4α=________.
【解析】tan 4α= .
答案:-
关键能力·合作学习
类型一 倍角公式的求值问题(数学运算)
【题组训练】
1.sin 10°sin 30°sin 50°sin 70°=________.
2.计算: =________.
3.已知cos ,α∈ ,则 =________.
【解析】1.原式=cos 80°cos 60°cos 40°cos 20°=
答案:
2.原式= .
答案:2
3.
=2cos =2sin ,
因为0<α< ,所以0< -α< ,
又 ,所以 ,
所以原式=2× .
答案:
【解题策略】
1.倍角公式正用、逆用解题的关注点
(1)注意观察式子的结构特点及角之间是否存在特殊的倍数关系,灵活正用或逆用倍角公式.
(2)结合诱导公式恰当变化函数名称,灵活处理系数,构造倍角公式的形式.
2.条件求值问题的解题实质
条件求值问题的解题实质是对已知条件与要求问题进行化简变形,最终代入已知条件求值;其解题突破口为已知条件与要求问题中角的特点,解题关键在于“变角”,即把“所求角”变为“已知角”.
【补偿训练】
(2020·沈阳高一检测)已知sin =
3cos(2π+α),其中α为锐角,
(1)求10sin2 的值;
(2)求 ·tan 2α的值.
【解析】化简sin =3cos(2π+α)得sin α=
3cos α,又因为sin2α+cos2α=1且α为锐角,
所以可得cos α= ,sin α= .
且由sin α=3cos α可得tan α=3.
(1)10sin2
=10sin2α- cos α-tan α
=10× -3=5.
(2)因为tan 2α= ;
cos 2α-sin 2α=cos2α-sin2α-2sin αcos α
,
所以 .
类型二 倍角公式的化简、证明问题(数学运算、逻辑推理) 角度1 化简问题
【典例】化简 =________.
【思路导引】结合二倍角公式化简求解.
【解析】原式=
=2|cos 4|-2|sin 4+cos 4|,
因为π<4< ,
所以cos 4<0,sin 4+cos 4<0.
所以原式=-2cos 4+2(sin 4+cos 4)=2sin 4.
答案:2sin 4
【变式探究】
化简 ,其中θ∈(0,π).
【解析】
原式=
①当θ∈ 时, ,
此时原式=sin +cos -cos +sin =2sin .
②当θ∈ 时, ∈ ,cos
角度2 恒等式证明问题
【典例】求证:cos2(A+B)-sin2(A-B)=cos 2Acos 2B.
【思路导引】可考虑从左向右证的思路:先把左边降幂扩角,再用余弦的和、差角公式转化为右边形式.
【证明】左边=
=
= (cos 2Acos 2B-sin 2Asin 2B+cos 2Acos 2B+
sin 2Asin 2B)=cos 2Acos 2B=右边,
所以等式成立.
【解题策略】
1.三角函数式的化简原则
三角函数式的化简原则:一是统一角,二是统一函数名.能求值的求值,必要时切化弦,更易通分、约分.
2.证明三角恒等式的原则与步骤
(1)观察恒等式两端的结构形式,处理原则是从复杂到简单,高次降低,复角化单角,如果两端都比较复杂,就将两端都化简,即采用“两头凑”的思想.
(2)证明恒等式的一般步骤
①先观察,找出角、函数名称、式子结构等方面的差异;
②本着“复角化单角”“异名化同名”“变换式子结构”“变量集中”等原则,设法消除差异,达到证明的目的.
【题组训练】
1.cos4 -sin4 的化简结果为 ( )
A.cos B.cos α C.cos 2α D.cos 4α
【解析】选B.cos4 -sin4
= =cos α.
2.化简: .
【解析】原式=
= =2.
3.求证: cos2θ(1-tan2θ)=cos 2θ.
【证明】方法一:左边=cos2θ
=cos2θ-sin2θ=cos 2θ=右边.故原式得证.
方法二:右边=cos 2θ=cos2θ-sin2θ
=cos2θ =cos2θ(1-tan2θ)=左边.故原式得证.
【补偿训练】
求证:
=tan .
【证明】左边=
=
=
= =右边,故原式得证.
类型三 倍角公式与三角函数性质的综合问题(逻辑推理)
【典例】已知函数f(x)=sin2x-sin2 ,x∈R.
(1)求f(x)的最小正周期.
(2)求f(x)在区间 上的最大值和最小值.
【解题策略】
倍角公式与三角函数性质的综合问题的解题策略
运用三角函数的和、差、倍角公式将函数关系式化成y=asin ωx+bcos ωx+k的形式,借助辅助角公式化为y=
Asin(ωx+φ)+k(或y=Acos(ωx+φ)+k)的形式,将ωx+φ看作一个整体研究函数的性质.
【跟踪训练】
已知函数f(x)=2 sin xcos x-2cos2x+1(x∈R).
(1)求函数f(x)的最小正周期及在区间 上的最大值和最小值.
(2)若f(x0)= ,x0∈ ,求cos 2x0的值.
【解析】(1)由f(x)=2 sin xcos x-2cos2x+1,
得f(x)= (2sin xcos x)-(2cos2x-1)
= sin 2x-cos 2x=2sin ,
所以函数f(x)的最小正周期为π.
易知f(x)=2sin 在区间 上为增函数,
在区间 上为减函数,
又f(0)=-1,f =2,f =-1,所以函数f(x)在 上的最大值为2,
最小值为-1.
(2)因为2sin ,所以sin .
又x0∈ ,所以2x0- ∈ ,
所以cos .
所以cos 2x0=cos
=cos
= .
【拓展延伸】
倍角公式的广义理解
对于二倍角公式有广义上的理解.如8α是4α的二倍角;6α是3α的二倍角;3α
是 α的二倍角; α是 α的二倍角;…….又如:α=2· ,
=2· ,…, =2· (n∈N*),
所以sin =2sin cos (n∈N*),
cos =cos2 -sin2 (n∈N*),
tan = (n∈N*).一般情况下,sin 2α≠2sin α,
只有当α=nπ(n∈Z)时,sin 2α=2sin α才成立,同样的cos 2α=2cos α,
tan 2α=2tan α在一般
情况下也不成立.
【拓展训练】
(2020·扬州高一检测)已知sin α+cos α= ,则sin 2α+cos 4α的
值为________.
【思路导引】先平方求出sin 2α,再利用二倍角公式求出cos 4α,即可求解.
【解析】因为sin α+cos α= ,
所以 =1+sin 2α= ,
即sin 2α=- ,
cos 4α=1-2sin22α=1-2× ,
sin 2α+cos 4α=- .
答案:
1.(2020·杭州高一检测)已知cos x= ,则cos 2x= ( )
【解析】选D.由cos x= 得cos 2x=2cos2x-1=2× -1= .
课堂检测·素养达标
2.若 ,则tan 2α等于 ( )
【解析】选B.因为 ,
所以 ,故tan α=-3,
所以根据倍角公式,得tan 2α= .
3.(教材二次开发:练习改编)(多选题)(2020·福州高一检测)若sin α>sin β
>0,则下列不等式中不一定成立的是 ( )
A.sin 2α>sin 2β B.cos 2α
cos 2β=1-2sin2β,
因为sin α>sin β>0,
所以sin2α>sin2β>0,-2sin2α<-2sin2β,
则1-2sin2α<1-2sin2β,
即cos 2α
当α= ,β= 时,
sin α>sin β>0,sin 2α=1> =sin 2β,
当α= ,β= 时,sin α>sin β>0,sin 2α=0< =sin 2β,
则AD可能成立,也可能不成立.
4.函数f(x)=sin -2 ·sin2x的最小正周期是________.
【解析】f(x)=sin -2 sin2x
= sin 2x- cos 2x-2 ×
= sin 2x+ cos 2x-
=sin ,
故最小正周期为π.
答案:π
5.(2020·铜川高一检测)已知cos β= ,sin(α-β)= ,且0<β<α< .
(1)求tan 2β的值;(2)求sin α的值.
【解析】(1)由cos β= ,0<β< ,得sin β=
则tan 2β= .
(2)由0<β<α< ,得0<α-β< ,
所以cos(α-β)= .
sin α=sin[(α-β)+β]
=sin(α-β)cos β+cos(α-β)sin β
= .
三十三 二倍角公式
【基础通关——水平一】 (15分钟 35分)
1.(2020·成都高一检测)设单位向量e= ,则cos 2α的值为 ( )
【解析】选A.由题设可得cos2α+ =1 cos2α= ,则cos 2α=2cos2α-
1= .
课时素养评价
2.已知sin 2θ=- ,则tan θ+ = ( )
【解析】选D.因为sin 2θ=2sin θcos θ=- ,
所以sin θcos θ=- ,
所以tan θ+ .
【补偿训练】
设sin α= ,tan(π-β)= ,则tan(α-2β)=( )
【解析】选D.因为sin α= ,α∈ ,
所以cos α=- ,所以tan α=- .
又tan(π-β)= ,所以tan β=- ,
所以tan 2β= .
所以tan(α-2β)= .
3.(2020·大理高一检测)已知角α+ 的终边与单位圆x2+y2=1交于P ,
则sin 2α等于 ( )
【解析】选A.由任意角三角函数定义可得sin ,则sin 2α=
-cos =2sin2 -1=- .
4.已知tan α= ,则cos2α+sin 2α的结果为________.
【解析】因为tan α= ,所以 ,
即2sin α=cos α,
所以sin2α+cos2α= cos2α+cos2α=1,
即cos2α= ,所以cos2α+sin 2α=cos2α+2sin α·cos α=2cos2α= .
答案:
5.(2020·广州高一检测)若sin ,则
cos =________.
【解析】已知sin ,且 ,则cos =
sin ,故cos =2cos2 -1=- .
答案:-
6.(2020·宁波高一检测)已知函数f(x)=
2sin x( cos x+sin x)-1.
(1)求f(x)的单调递增区间;
(2)若f ,求sin 的值.
【解析】(1)f(x)=2 sin xcos x+2sin2x-1= sin 2x-cos 2x=2sin ,
令- +2kπ≤2x- ≤ +2kπ,k∈Z,解得- +kπ≤x≤ +kπ,
k∈Z,
故单调递增区间为 (k∈Z).
(2)由f 得sin ,
则sin =sin =cos =1-2sin2 .
【能力进阶——水平二】 (30分钟 60分)
一、单选题(每小题5分,共20分)
1.若sin α+cos α= ,0<α<π,则sin 2α+cos 2α= ( )
【解析】选A.因为sin α+cos α= ,①
所以1+2sin αcos α= ,
即2sin αcos α=sin 2α=- ,
所以1-2sin αcos α=(sin α-cos α)2= .
因为sin αcos α<0,且0<α<π,
所以sin α>0,cos α<0,
所以sin α-cos α= .②
①×②变形得cos2α-sin2α=cos 2α=- ,
所以sin 2α+cos 2α=- .
2.(2020·全国Ⅰ卷)已知α∈(0,π),且3cos 2α-8cos α=5,则sin α= ( )
【解析】选A.由3cos 2α-8cos α=5,
得6cos2α-8cos α-8=0,
即3cos2α-4cos α-4=0,
解得cos α=- 或cos α=2(舍去),
又因为α∈(0,π),所以sin α= .
【补偿训练】
(2020·合肥高一检测)若cos ,则cos = ( )
【解析】选C.cos =cos
=cos =cos
=2cos2 -1=2× -1=- .
3.(2020·石家庄高一检测)若角α∈ ,β∈ , sin β=cos -sin ,sin α= ,则cos β= ( )
【解析】选A.由题意可得sin β=sin .
因为 ∈ ,β∈ ,
所以 =β,则2β= -α,
所以cos 2β=cos =sin α= ,
又cos 2β=2cos2β-1= ,解得cos2β= ,
又β∈ ,所以cos β= .
4.(2020·合肥高一检测)已知函数f(x)=sin(x+φ+θ)的图象关于直线x=π对称,其中0<φ<π,- <θ<0,且tan θ=-2,则sin 2φ的值为 ( )
【解析】选D.因为函数f(x)=sin(x+φ+θ)的图象关于直线x=π对称,所以由正弦函数的图象与性质可知π+φ+θ= +kπ,k∈Z,
则θ=- -φ+kπ,k∈Z,
所以tan θ= =-2,
即tan =2,故 =2,化简得cos φ=-2sin φ,又sin2φ+cos2φ=1 ,
解得sin2φ= ,
因为0<φ<π,所以sin φ>0,则sin φ= ,而由cos φ=-2sin φ,可得cos φ
= ,
所以sin 2φ=2sin φcos φ=2× × =- .
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错
的得0分)
5.(2020·盐城高一检测)下列各式中,值为 的是 ( )
A.sin 15°cos 15° B.cos2 -sin2
C. D.
【解析】选CD.因为sin 15°cos 15°= sin 30°
= × = ,所以A不正确;
因为cos2 -sin2
=cos ,所以B不正确;
因为 ,所以C正确;
因为 ,所以D正确.
6.在△ABC中,若acos A=bcos B,则△ABC的形状可能为 ( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
【解析】选ABCD.根据正弦定理 ,
因为 acos A=bcos B,
所以sin Acos A=sin Bcos B,
即sin 2A=sin 2B.
因为2A,2B∈(0,2π),
所以2A=2B或2A+2B=π,即A=B或A+B= ,
所以△ABC可能为:直角三角形,等腰三角形,等腰直角三角形,等边三角形.
三、填空题(每小题5分,共10分)
7.函数y=sin xcos x+ cos2x- 的图象的一个对称中心为________.
【解析】y= sin 2x+ (1+cos 2x)-
= sin 2x+ cos 2x- =sin - ,
令2x+ =kπ,x= (k∈Z),
当k=1时,x= ,对称中心是 ;
当k=2时,x= ,对称中心是 .
答案: (答案不唯一)
【补偿训练】
已知函数f(x)= cos2x-sin xcos x- ,则f =________;函数f(x)
在 上的值域为________.
【解析】由题可知f(x)= cos2x-sin xcos x- ,
则f(x)=
= cos 2x- sin 2x,
所以f(x)=cos ,
则f =cos =0,
因为x∈ ,所以2x+ ∈ ,
又函数y=cos t在 上单调递减,在 上单调递增,当2x+ =π,
即x= 时,f(x)min=cos π=-1.
当2x+ = ,
即x=0时,f(x)max=cos = .
所以函数f(x)在 上的值域为 .
答案:0
8.已知cos ,
【解析】
=
=sin 2x·tan ,
因为
所以sin .
所以tan .
所以cos x=cos
=cos cos +sin sin = .
sin x=sin
=sin cos -sin cos
= ,
可得sin 2x=2sin xcos x=2× .
所以 .
答案:
四、解答题(每小题10分,共20分)
9.已知sin -2cos =0.
求 的值.
【解析】由sin -2cos =0,知cos ≠0,
所以tan =2,
所以tan x= .
所以
= =
=
= .
10.(2020·扬州高一检测)从秦朝统一币制到清朝末年,圆形方孔铜钱(简称“孔方兄”)是我国使用时间长达两千多年的货币.如图1,这是一枚清朝同治年间的铜钱,其边框是由大小不等的两同心圆围成的,内嵌正方形孔的中心与同心圆圆心重合,正方形外部,圆框内部刻有四个字“同治重宝”.某模具厂计划仿制这样的铜钱作为纪念品,其小圆内部图纸设计如图2所示,小圆直径1厘米,内嵌一个大正方形孔,四周是四个全等的小正方形(边长比孔的边长小),每个正方形有两个顶点在圆周上,另两个顶点在孔边上,四个小正方形内用于刻铜钱上的字.设∠OAB=θ,五个正方形的面积和为S.
(1)求面积S关于θ的函数表达式,并求定义域;
(2)求面积S的最小值及此时tan θ的值.
【解析】(1)过点O分别作小正方形边、大正方形边的垂线,垂足分别为E,F,
因为内嵌一个大正方形孔的中心与同心圆圆心重合,所以点E,F分别为小正方
形和大正方形边的中点,所以小正方形的边长为 ×2=sin θ,大正方形
的边长为 ×2=cos θ-2sin θ,
所以五个正方形的面积和为S=4sin2θ+
=8sin2θ+cos2θ-4sin θcos θ,
因为小正方形边长小于内嵌一个大正方形的边长,
所以sin θ
所以面积S关于θ的函数表达式为S=8sin2θ+cos2θ-4sin θcos θ,
θ的取值范围为 ,tanθ0= ,θ0∈ .
(2)方法一:S=8sin2θ+cos2θ-4sin θcos θ
=8× -2sin 2θ
=
= ,其中tan φ= ,φ∈ ,
所以Smin= ,此时sin =1,因为θ∈ ,
所以0<2θ+φ<2θ0+ < π,
所以2θ+φ= ,
所以tan 2θ=tan ,
则tan 2θ= ,
化简得:2tan2θ+7tan θ-2=0,由此解得tan θ= ,
因为0
故面积S最小值为 ,此时tan θ= .
【创新迁移】
1.(2020·合肥高一检测)1626年,阿贝尔特格洛德最早推出简写的三角符
号:sin,tan,sec(正割),1675年,英国人奥屈特最早推出余下的简写三角符
号:cos,cot,csc(余割),但直到1748年,经过数学家欧拉的引用后,才逐渐通用
起来,其中secθ= ,csc θ= .若α∈(0,π),且 =2,则
tan α= ( )
【解析】选D.因为3sin α+2cos α=2,
所以 =2,
所以 =2,
所以3tan +1-tan2 =tan2 +1,解得tan =0或 .
又因为α∈(0,π),
所以tan >0,
所以tan = ,
则tan α= .
2.在△ABC中,设向量m=(sin A,cos B),n=(sin B,cos A)且m∥n,m≠n.
(1)求证:A+B= .
(2)求sin A+sin B的取值范围.
(3)若(sin Asin B)x=sin A+sin B,试确定实数x的取值范围.
【解析】(1)因为向量m=(sin A,cos B),n=(sin B,cos A)且m∥n,
所以sin Acos A-sin Bcos B=0,即sin 2A=sin 2B,解得2A=2B或2A+2B=π,
化简可得A=B,或A+B= ,但A=B时有m=n,与已知矛盾,故舍去,故有A+B= .
(2)由(1)可知A+B= ,故sin A+sin B
=sin A+sin =sin A+cos A
= sin ,
因为0
(3)由题意可知x= ,
设sin A+cos A=t∈(1, ],则t2=1+2sin Acos A,
故sin Acos A= ,代入得x= ,
故实数x的取值范围为[2 ,+∞).
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
