1.3探索三角形全等的条件(1) 课件(共25张PPT)
文档属性
| 名称 | 1.3探索三角形全等的条件(1) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 12:38:58 | ||
图片预览








文档简介
(共25张PPT)
七年级数学(上)(第一章)
1.3判定三角形全等的条件(1)
【创设情境,导入新课】
想一想:
1.要画一个三角形与已知的三角形全等,需要几个条件?
2.只给一个或两个条件能画出一个三角形与已知的三角形全等吗?
【教学目标】
1.经历探索三角形全等“边边边”的条件过程,
理解并会应用“边边边”说明两个三角形全等;
2.认识三角形的稳定性.
自主学习,预习诊断
(1)什么叫全等三角形?
(2)全等三角形有什么性质?
(3)判定三角形全等至少需要几个条件?
【课中实施】
合作探究,展示交流
1.议一议:
只给一个或两个条件能画出一个三角形与
已知的三角形全等吗?
寻求判别三角形全等的条件
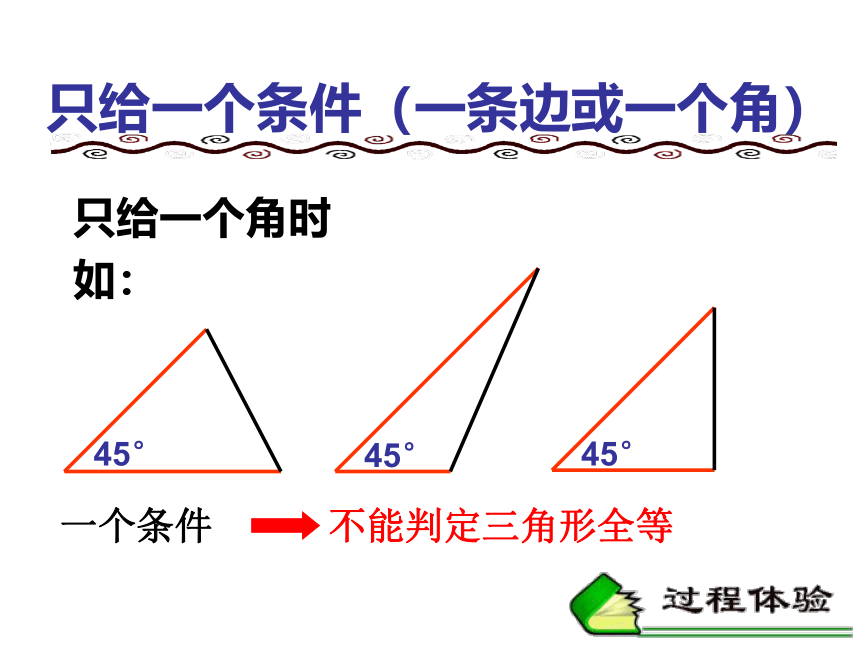
只给一个条件(一条边或一个角)
只给一条边时
如:
3cm
3cm
3cm
只给一个角时
如:
45°
45°
45°
只给一个条件(一条边或一个角)
一个条件
不能判定三角形全等
如果三角形的一条边为3cm,一个内角为30°
3cm
3cm
3cm
30°
30°
30°
给出两个条件时(一边及一角)
给出两个条件时(已知两角)
如果三角形两个内角分别为30°,45°时
30°
45°
30°
45°
30°
45°
给出两个条件时(已知两边)
如果三角形的两边分别为4cm,6cm 时
6cm
4cm
4cm
两个条件
不能判定三角形全等
议一议:
如果给出三个条件画三角形,那么有哪种
可能的情况?
寻求判别三角形全等的条件
寻求判别三角形全等的条件
三个条件
边边边
角角角
两角一边
两边一角
2.做一做:(自己动手)
(1)已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?
把你画的三角形与同伴画的进行比较,它们一定全等吗?
(2)用三根长度分别是4cm,5cm和7cm的三根木棒摆一个三角形,把你摆出的三角形与同伴摆出的进行比较,它们一定全等吗?
通过上面的动手操作,你能得出的结论是:
判定三角形全等的方法1.
三边分别相等的两个三角形全等
简写为:“边边边”或“SSS”
A
B
C
A
B
C
三边分别相等的两个三角形全等.
(简写成“边边边”或“SSS”)
如何用符号语言来表达呢
≌
结论
例题展示
例1.如图1-29,在△ABC 中,AB= AC ,
AD是中线, △ABD △ACD全等吗?
为什么?
随堂练习
1.已知:如图,A、B、E、F在一条直线上,且AC=BD,CE=DF,AF=BE。
△ACE与△BDF全等吗?为什么?
练一练:
2.如图所示, 在四边形ABCD中, AD=BC, AB=CD,试说明△ABC ≌ △CDA.
A
B
C
D
取出若干根的木条,把它们分别做成三角形和四边形框架,并拉动它们.
你发现什么?
三角形的大小和形状是固定不变的,
而四边形的形状会改变.
3.做一做
动 动 手
图1-27是用三根木条钉成的
一个三角形框架,它的大小
和形状是固定不变的,
三角形的这个性质叫
三角形稳定性.
图1-28是用四根木条钉成的
一个三角形框架,它的形状是可以改变的,
它不具有稳定性.
三角形的稳定性举例
课堂小结
通过这节课的学习,
你有什么收获?
【当堂达标】
见本节导学案“当堂达标 ”
【布置作业】
习题1.7第2、3题
七年级数学(上)(第一章)
1.3判定三角形全等的条件(1)
【创设情境,导入新课】
想一想:
1.要画一个三角形与已知的三角形全等,需要几个条件?
2.只给一个或两个条件能画出一个三角形与已知的三角形全等吗?
【教学目标】
1.经历探索三角形全等“边边边”的条件过程,
理解并会应用“边边边”说明两个三角形全等;
2.认识三角形的稳定性.
自主学习,预习诊断
(1)什么叫全等三角形?
(2)全等三角形有什么性质?
(3)判定三角形全等至少需要几个条件?
【课中实施】
合作探究,展示交流
1.议一议:
只给一个或两个条件能画出一个三角形与
已知的三角形全等吗?
寻求判别三角形全等的条件
只给一个条件(一条边或一个角)
只给一条边时
如:
3cm
3cm
3cm
只给一个角时
如:
45°
45°
45°
只给一个条件(一条边或一个角)
一个条件
不能判定三角形全等
如果三角形的一条边为3cm,一个内角为30°
3cm
3cm
3cm
30°
30°
30°
给出两个条件时(一边及一角)
给出两个条件时(已知两角)
如果三角形两个内角分别为30°,45°时
30°
45°
30°
45°
30°
45°
给出两个条件时(已知两边)
如果三角形的两边分别为4cm,6cm 时
6cm
4cm
4cm
两个条件
不能判定三角形全等
议一议:
如果给出三个条件画三角形,那么有哪种
可能的情况?
寻求判别三角形全等的条件
寻求判别三角形全等的条件
三个条件
边边边
角角角
两角一边
两边一角
2.做一做:(自己动手)
(1)已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?
把你画的三角形与同伴画的进行比较,它们一定全等吗?
(2)用三根长度分别是4cm,5cm和7cm的三根木棒摆一个三角形,把你摆出的三角形与同伴摆出的进行比较,它们一定全等吗?
通过上面的动手操作,你能得出的结论是:
判定三角形全等的方法1.
三边分别相等的两个三角形全等
简写为:“边边边”或“SSS”
A
B
C
A
B
C
三边分别相等的两个三角形全等.
(简写成“边边边”或“SSS”)
如何用符号语言来表达呢
≌
结论
例题展示
例1.如图1-29,在△ABC 中,AB= AC ,
AD是中线, △ABD △ACD全等吗?
为什么?
随堂练习
1.已知:如图,A、B、E、F在一条直线上,且AC=BD,CE=DF,AF=BE。
△ACE与△BDF全等吗?为什么?
练一练:
2.如图所示, 在四边形ABCD中, AD=BC, AB=CD,试说明△ABC ≌ △CDA.
A
B
C
D
取出若干根的木条,把它们分别做成三角形和四边形框架,并拉动它们.
你发现什么?
三角形的大小和形状是固定不变的,
而四边形的形状会改变.
3.做一做
动 动 手
图1-27是用三根木条钉成的
一个三角形框架,它的大小
和形状是固定不变的,
三角形的这个性质叫
三角形稳定性.
图1-28是用四根木条钉成的
一个三角形框架,它的形状是可以改变的,
它不具有稳定性.
三角形的稳定性举例
课堂小结
通过这节课的学习,
你有什么收获?
【当堂达标】
见本节导学案“当堂达标 ”
【布置作业】
习题1.7第2、3题
