第二章 解直角三角形检测试题(含答案)
文档属性
| 名称 | 第二章 解直角三角形检测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 236.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 14:30:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
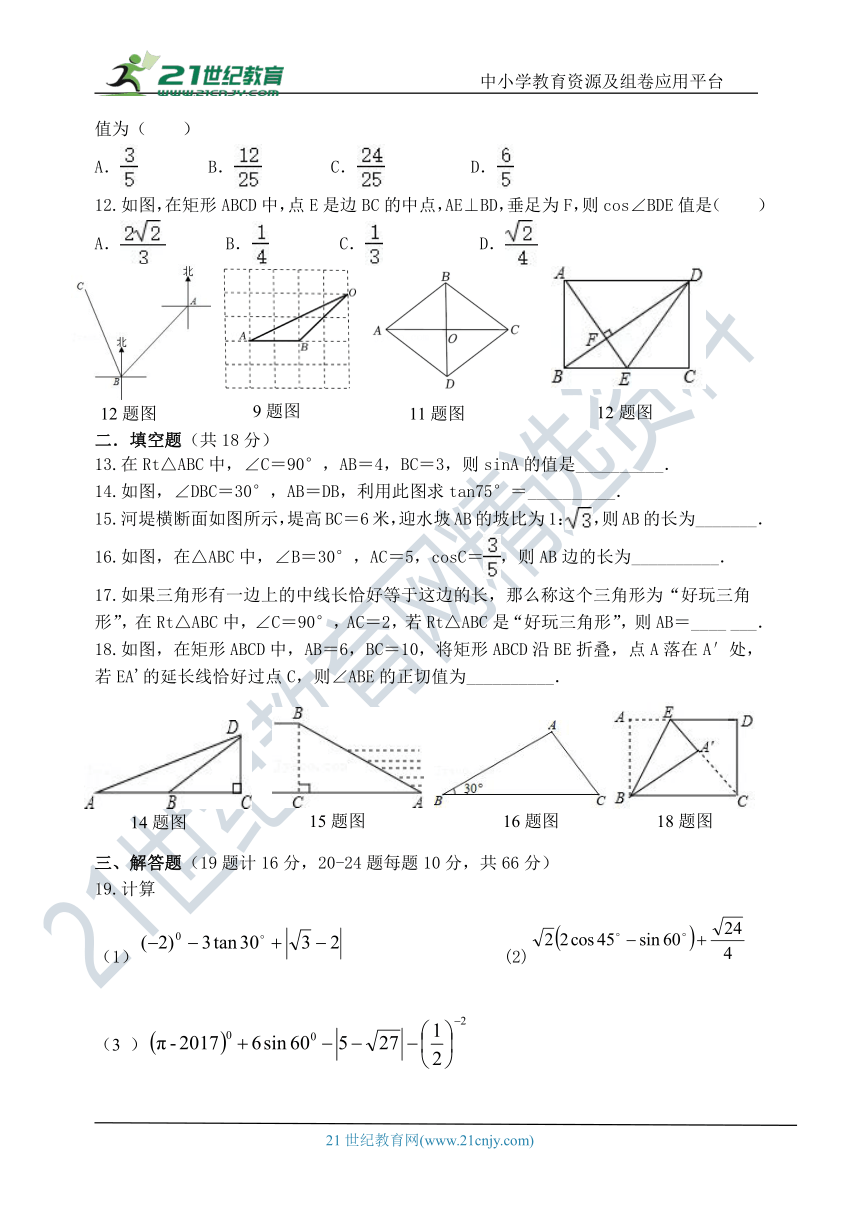
第二章《解直角三角形》单元测试题B
时间90分钟,满分120分
一.选择题(共36分)
1.等腰三角形的底边长10cm,周长为36cm,则底角的正弦值为( )
A. B. C. D.
2.一架长5m的梯子斜靠在墙上,测得它与地面的夹角是65°,则梯子顶端到地面的距离为( )
A.5sin65°m B.5cos65°m C.m D.m
3.已知一道斜坡的坡比为1:,坡长为24米,那么坡高为( )米.
A. B.12 C. D.6
4.若sin(70°﹣α)=cos50°,则α的度数是( )
A.20° B.30° C.40° D.50°
5.在Rt△ABC中,∠C=90°,若AB=10,sinA=,则斜边上的高等于( )
A.5 B.4.8 C.4.6 D.4
6.跳伞运动员小李在200米的空中测得地面上的着落点A的俯角为60°,那么此时小李离着落点A的距离是( )
A.200米 B.400米 C.米 D.米
7.在Rt△ABC中,∠B=90°,cosA=,则sinA=( )
A. B. C. D.
8.一艘轮船由海平面上A地出发向南偏西40°的方向行驶100海里到达B地,再由B地向北偏西20°的方向行驶100海里到达C地,则A,C两地相距( )
A.100海里 B.80海里 C.60海里 D.40海里
9.如图,在由小正方形组成的网格中,小正方形的边长均为1,点A,B,O都在小正方形的顶点上,则∠AOB的正弦值是( )
A. B. C. D.
10.在△ABC中,∠A,∠B为锐角,且有|sinA﹣|+(﹣cosB)2=0,则这个三角形是( )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.等边三角形
11.如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,则∠BAD的正弦值为( )
A. B. C. D.
12.如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则cos∠BDE值是( )
A. B. C. D.
二.填空题(共18分)
13.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sinA的值是__________.
14.如图,∠DBC=30°,AB=DB,利用此图求tan75°=__________.
15.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1:,则AB的长为_______.
16.如图,在△ABC中,∠B=30°,AC=5,cosC=,则AB边的长为__________.
17.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,AC=2,若Rt△ABC是“好玩三角形”,则AB=____ ___.
18.如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处,若EA'的延长线恰好过点C,则∠ABE的正切值为__________.
三、解答题(19题计16分,20-24题每题10分,共66分)
19.计算
(1) (2)
(3 )
(4)6sin45°﹣|1﹣|﹣×(π﹣2022)0﹣()﹣2.
20.直线y=2x+3交x轴于A,交y轴于B,求∠ABO的三角比.
21.在Rt△ABC中,∠C=90°,AB=10,cos∠ABC=,D是AC上一点,且∠DBC=30°,求BC、AD的长.
22.如图,从热气球C上测得两建筑物A、B底部的俯角分别为29.5°和45°,如果这时气球的高度CD为80米,且点A、D、B在同一直线上,求建筑物A、B之间的距离(结果精确到1米).[参考数据:sin29.5°≈0.49,cos29.5°≈0.87,tan29.5°≈0.57]
23.如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)
24.如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果保留根号)
第二章《解直角三角形》单元测试题
参考答案与试题解析
一.选择题(共12小题)
1-5.DABBB. 6-10.DAABD.11-12.CA.
二.填空题(共6小题)
13.; 14.2+; 15.12米;
16.8; 17.或; 18..
三.解答题(共6小题)
19.(1);(2)2;(3)2;(4)﹣3.
20.解:∵直线y=2x+3交x轴于A,
交y轴于B,
∴y=0时,2x+3=0,解得:x=﹣,
x=0时,y=3,则A(﹣,0),B(0,3),
则AO=,BO=3,
故AB=,
故sin∠ABO==,
cos∠ABO===,
tan∠ABO==.
21.解:∵cos∠ABC=,∠C=90°,
∴=,
∵AB=10,
∴BC=10×=6,
∴AC==8,
∵∠DBC=30°,
∴CD=BC tan30°=6×=6,
∴AD=AC﹣CD=8﹣6.
22.解:由已知得:∠ECA=29.5°,∠FCB=45°,CD=80米,EF∥AB,CD⊥AB,
∴∠A=∠ECA=29.5°,∠B=∠FCB=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=80米,
在Rt△ACD中,∠CDA=90°,tanA=,
∴AD==≈140.4(米),
∴AB=AD+BD≈140.4+80≈220(米),
即建筑物A、B之间的距离约为220米.
23.解:设CE的长为xm,
在Rt△CBE中,∵∠CBE=45°,
∴∠BCD=45°,
∴CE=BE=xm,
∴AE=AB+BE=40+x(m)
在Rt△ACE中,∵∠CAE=30°,
∴tan30°=
即=,
解得,x=20+20
≈20×1.732+20
=54.64(m)
所以CD=CE+ED
=54.65+1.5=56.15≈56(m)
答:该建筑物的高度约为56m.
24.解:过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
则DE=BF=CH=10m,
在Rt△ADF中,AF=AB﹣BF=70m,∠ADF=45°,
∴DF=AF=70m.
在Rt△CDE中,DE=10m,∠DCE=30°,
∴CE===10(m),
∴BC=BE﹣CE=(70﹣10)m.
答:障碍物B,C两点间的距离为(70﹣10)m.
12题图
11题图
9题图
12题图
14题图
15题图
16题图
18题图
22题图
23题图
24题图
PAGE
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二章《解直角三角形》单元测试题B
时间90分钟,满分120分
一.选择题(共36分)
1.等腰三角形的底边长10cm,周长为36cm,则底角的正弦值为( )
A. B. C. D.
2.一架长5m的梯子斜靠在墙上,测得它与地面的夹角是65°,则梯子顶端到地面的距离为( )
A.5sin65°m B.5cos65°m C.m D.m
3.已知一道斜坡的坡比为1:,坡长为24米,那么坡高为( )米.
A. B.12 C. D.6
4.若sin(70°﹣α)=cos50°,则α的度数是( )
A.20° B.30° C.40° D.50°
5.在Rt△ABC中,∠C=90°,若AB=10,sinA=,则斜边上的高等于( )
A.5 B.4.8 C.4.6 D.4
6.跳伞运动员小李在200米的空中测得地面上的着落点A的俯角为60°,那么此时小李离着落点A的距离是( )
A.200米 B.400米 C.米 D.米
7.在Rt△ABC中,∠B=90°,cosA=,则sinA=( )
A. B. C. D.
8.一艘轮船由海平面上A地出发向南偏西40°的方向行驶100海里到达B地,再由B地向北偏西20°的方向行驶100海里到达C地,则A,C两地相距( )
A.100海里 B.80海里 C.60海里 D.40海里
9.如图,在由小正方形组成的网格中,小正方形的边长均为1,点A,B,O都在小正方形的顶点上,则∠AOB的正弦值是( )
A. B. C. D.
10.在△ABC中,∠A,∠B为锐角,且有|sinA﹣|+(﹣cosB)2=0,则这个三角形是( )
A.等腰三角形 B.直角三角形 C.钝角三角形 D.等边三角形
11.如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,则∠BAD的正弦值为( )
A. B. C. D.
12.如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则cos∠BDE值是( )
A. B. C. D.
二.填空题(共18分)
13.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sinA的值是__________.
14.如图,∠DBC=30°,AB=DB,利用此图求tan75°=__________.
15.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1:,则AB的长为_______.
16.如图,在△ABC中,∠B=30°,AC=5,cosC=,则AB边的长为__________.
17.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,AC=2,若Rt△ABC是“好玩三角形”,则AB=____ ___.
18.如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处,若EA'的延长线恰好过点C,则∠ABE的正切值为__________.
三、解答题(19题计16分,20-24题每题10分,共66分)
19.计算
(1) (2)
(3 )
(4)6sin45°﹣|1﹣|﹣×(π﹣2022)0﹣()﹣2.
20.直线y=2x+3交x轴于A,交y轴于B,求∠ABO的三角比.
21.在Rt△ABC中,∠C=90°,AB=10,cos∠ABC=,D是AC上一点,且∠DBC=30°,求BC、AD的长.
22.如图,从热气球C上测得两建筑物A、B底部的俯角分别为29.5°和45°,如果这时气球的高度CD为80米,且点A、D、B在同一直线上,求建筑物A、B之间的距离(结果精确到1米).[参考数据:sin29.5°≈0.49,cos29.5°≈0.87,tan29.5°≈0.57]
23.如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)
24.如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果保留根号)
第二章《解直角三角形》单元测试题
参考答案与试题解析
一.选择题(共12小题)
1-5.DABBB. 6-10.DAABD.11-12.CA.
二.填空题(共6小题)
13.; 14.2+; 15.12米;
16.8; 17.或; 18..
三.解答题(共6小题)
19.(1);(2)2;(3)2;(4)﹣3.
20.解:∵直线y=2x+3交x轴于A,
交y轴于B,
∴y=0时,2x+3=0,解得:x=﹣,
x=0时,y=3,则A(﹣,0),B(0,3),
则AO=,BO=3,
故AB=,
故sin∠ABO==,
cos∠ABO===,
tan∠ABO==.
21.解:∵cos∠ABC=,∠C=90°,
∴=,
∵AB=10,
∴BC=10×=6,
∴AC==8,
∵∠DBC=30°,
∴CD=BC tan30°=6×=6,
∴AD=AC﹣CD=8﹣6.
22.解:由已知得:∠ECA=29.5°,∠FCB=45°,CD=80米,EF∥AB,CD⊥AB,
∴∠A=∠ECA=29.5°,∠B=∠FCB=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=80米,
在Rt△ACD中,∠CDA=90°,tanA=,
∴AD==≈140.4(米),
∴AB=AD+BD≈140.4+80≈220(米),
即建筑物A、B之间的距离约为220米.
23.解:设CE的长为xm,
在Rt△CBE中,∵∠CBE=45°,
∴∠BCD=45°,
∴CE=BE=xm,
∴AE=AB+BE=40+x(m)
在Rt△ACE中,∵∠CAE=30°,
∴tan30°=
即=,
解得,x=20+20
≈20×1.732+20
=54.64(m)
所以CD=CE+ED
=54.65+1.5=56.15≈56(m)
答:该建筑物的高度约为56m.
24.解:过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
则DE=BF=CH=10m,
在Rt△ADF中,AF=AB﹣BF=70m,∠ADF=45°,
∴DF=AF=70m.
在Rt△CDE中,DE=10m,∠DCE=30°,
∴CE===10(m),
∴BC=BE﹣CE=(70﹣10)m.
答:障碍物B,C两点间的距离为(70﹣10)m.
12题图
11题图
9题图
12题图
14题图
15题图
16题图
18题图
22题图
23题图
24题图
PAGE
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
