2023届高考数学二轮专题复习:复数的三角表示式 课件(共16张PPT)
文档属性
| 名称 | 2023届高考数学二轮专题复习:复数的三角表示式 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 17:11:02 | ||
图片预览




文档简介
(共16张PPT)
7.3.1 复数的三角表示式
第七章 复数
2023/3/24
复数四则运算
设z1=+b,z2=c+d (,b,c,∈R),则
新知引入
复数四则运算
设z1=+b,z2=c+d (,b,c,∈R),则
+=
-=
=
==
加
减
乘
除
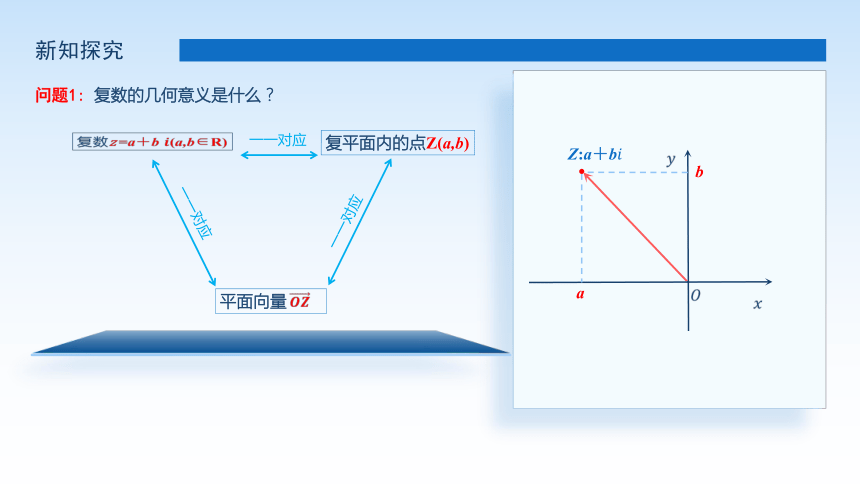
问题1: 复数的几何意义是什么?
新知探究
问题1: 复数的几何意义是什么?
复数z =a+b (a,b∈R)
复平面内的点Z(a,b)
一一对应
一一对应
一一对应
平面向量
a
b
Z:a+b
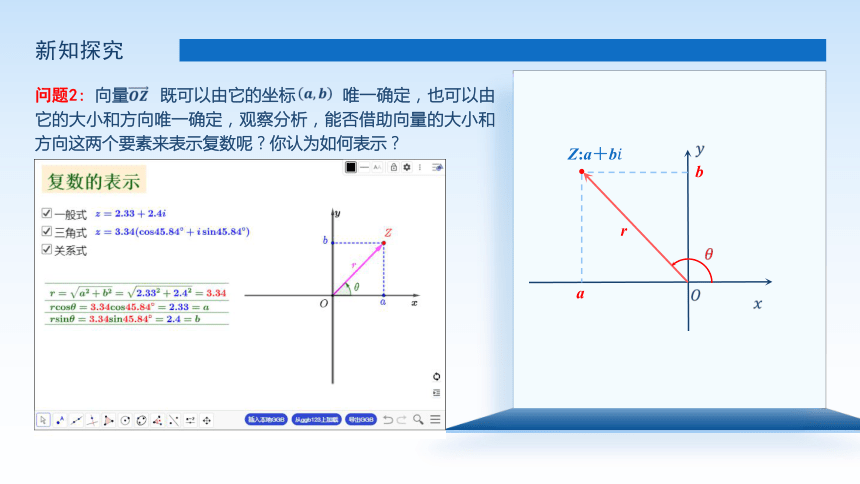
问题2: 向量 既可以由它的坐标 唯一确定,也可以由它的大小和方向唯一确定,观察分析图1,能否借助向量的大小和方向这两个要素来表示复数呢?你认为如何表示?
新知探究
a
b
Z:a+b
问题2: 向量 既可以由它的坐标 唯一确定,也可以由它的大小和方向唯一确定,观察分析,能否借助向量的大小和方向这两个要素来表示复数呢?你认为如何表示?
r
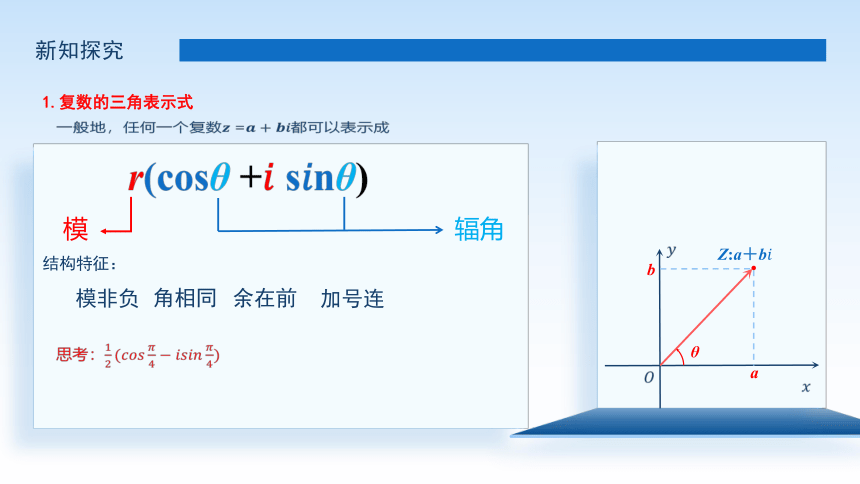
1.复数的三角表示式
新知探究
一般地,任何一个复数= 都可以表示成
1.复数的三角表示式
辐角
模
θ 是以x轴的非负半轴为始边,向量所在射线为终边的角,叫做复数= 的辐角;
r是复数;
结构特征:
模非负
a
b
Z:a+b
θ
角相同
余在前
加号连
思考:
新知探究
辐角
模
θ 是以x轴的非负半轴为始边,向量所在射线为终边的角,叫做复数= 的辐角;
r是复数;
① r ≥0
② θ 在前后一致,可为任意值
③ cos θ 在前,s n 在后
④ 中间用加号连接
表现形式:
a+b 叫做复数的代数表示式,简称代数形式.
r(cosθ+ s nθ) 叫做复数的三角表示式,简称三角形式;
a
b
Z:a+b
θ
一般地,任何一个复数= 都可以表示成
1.复数的三角表示式
问题3: 一个复数的辐角的值有多少个?这些辐角的值之间有什么关系呢?
新知探究
问题3: 一个非零复数的辐角的值有多少个?这些辐角的值之间有什么关系呢?
无数多个
相差2π的整数倍
若复数为0,它的辐角是哪个角?
复数0对应零向量,零向量的方向是任意的,所以复数0的辐角也是任意的,而不是0。
a
b
Z:a+b
θ
问题4: 在研究问题时,复数辐角的多值性有时会给我们带来不便,为了使任意一个非0复数有唯一确定的“值”作为其所有辐角值的代表,你认为规定这种“值”在哪个范围内比较合适?
0≤θ<2π
2.辐角与辐角主值
新知探究
我们规定在范围内的辐角θ的值为辐角的主值.通常记作,即.
2.辐角与辐角主值
a
b
Z:a+b
θ
每个非零复数的幅角的主值有且只有一个
例如:
3. 复数代数形式和三角形式的转化
例题讲解
例1 画出下列复数对应的向量,并把这些复数表示成三角形式。
3. 复数代数形式和三角形式的转化
a
b
⑴
⑵
(
例题讲解
例1 画出下列复数对应的向量,并把这些复数表示成三角形式。
3. 复数代数形式和三角形式的转化
b
⑴
⑵
θ
例题讲解
复数的代数形式转化成三角形式的基本步骤:
(1)求复数的模:
(2)求复数的辐角的主值:
(3)写出复数的三角形式:
例题讲解
例2 分别指出下列复数的模和一个辐角,画出它们对应向量的,并把这些复数表示成代数形式.
复数三角形式转化成代数形式的基本步骤:
例题讲解
复数三角形式转化成代数形式的基本步骤:
课堂小结
复数的几何意义
复数的三角表示式
复数的辐角与辐角主值
复数代数形式与三角形式的互化
三角函数的概念
谢谢大家!
7.3.1 复数的三角表示式
第七章 复数
2023/3/24
复数四则运算
设z1=+b,z2=c+d (,b,c,∈R),则
新知引入
复数四则运算
设z1=+b,z2=c+d (,b,c,∈R),则
+=
-=
=
==
加
减
乘
除
问题1: 复数的几何意义是什么?
新知探究
问题1: 复数的几何意义是什么?
复数z =a+b (a,b∈R)
复平面内的点Z(a,b)
一一对应
一一对应
一一对应
平面向量
a
b
Z:a+b
问题2: 向量 既可以由它的坐标 唯一确定,也可以由它的大小和方向唯一确定,观察分析图1,能否借助向量的大小和方向这两个要素来表示复数呢?你认为如何表示?
新知探究
a
b
Z:a+b
问题2: 向量 既可以由它的坐标 唯一确定,也可以由它的大小和方向唯一确定,观察分析,能否借助向量的大小和方向这两个要素来表示复数呢?你认为如何表示?
r
1.复数的三角表示式
新知探究
一般地,任何一个复数= 都可以表示成
1.复数的三角表示式
辐角
模
θ 是以x轴的非负半轴为始边,向量所在射线为终边的角,叫做复数= 的辐角;
r是复数;
结构特征:
模非负
a
b
Z:a+b
θ
角相同
余在前
加号连
思考:
新知探究
辐角
模
θ 是以x轴的非负半轴为始边,向量所在射线为终边的角,叫做复数= 的辐角;
r是复数;
① r ≥0
② θ 在前后一致,可为任意值
③ cos θ 在前,s n 在后
④ 中间用加号连接
表现形式:
a+b 叫做复数的代数表示式,简称代数形式.
r(cosθ+ s nθ) 叫做复数的三角表示式,简称三角形式;
a
b
Z:a+b
θ
一般地,任何一个复数= 都可以表示成
1.复数的三角表示式
问题3: 一个复数的辐角的值有多少个?这些辐角的值之间有什么关系呢?
新知探究
问题3: 一个非零复数的辐角的值有多少个?这些辐角的值之间有什么关系呢?
无数多个
相差2π的整数倍
若复数为0,它的辐角是哪个角?
复数0对应零向量,零向量的方向是任意的,所以复数0的辐角也是任意的,而不是0。
a
b
Z:a+b
θ
问题4: 在研究问题时,复数辐角的多值性有时会给我们带来不便,为了使任意一个非0复数有唯一确定的“值”作为其所有辐角值的代表,你认为规定这种“值”在哪个范围内比较合适?
0≤θ<2π
2.辐角与辐角主值
新知探究
我们规定在范围内的辐角θ的值为辐角的主值.通常记作,即.
2.辐角与辐角主值
a
b
Z:a+b
θ
每个非零复数的幅角的主值有且只有一个
例如:
3. 复数代数形式和三角形式的转化
例题讲解
例1 画出下列复数对应的向量,并把这些复数表示成三角形式。
3. 复数代数形式和三角形式的转化
a
b
⑴
⑵
(
例题讲解
例1 画出下列复数对应的向量,并把这些复数表示成三角形式。
3. 复数代数形式和三角形式的转化
b
⑴
⑵
θ
例题讲解
复数的代数形式转化成三角形式的基本步骤:
(1)求复数的模:
(2)求复数的辐角的主值:
(3)写出复数的三角形式:
例题讲解
例2 分别指出下列复数的模和一个辐角,画出它们对应向量的,并把这些复数表示成代数形式.
复数三角形式转化成代数形式的基本步骤:
例题讲解
复数三角形式转化成代数形式的基本步骤:
课堂小结
复数的几何意义
复数的三角表示式
复数的辐角与辐角主值
复数代数形式与三角形式的互化
三角函数的概念
谢谢大家!
同课章节目录
