第五章 圆单元测试题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章《圆》单元测试题A
时间90分钟,满分120分
一.选择题(共36分)
1.以已知点O为圆心,已知线段a为半径作圆,可以作( )
A.1个 B.2个 C.3个 D.无数个
2.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A. B. C. D.
3.四边形ABCD内接于⊙O,BC是⊙O的直径,若∠ADC=120°,则∠ACB等于( )
A.30° B.40° C.60° D.80°
4.下列命题是真命题的个数是( )
①直径所对的角是90°;②三点确定一个圆;③圆的切线垂直于过切线的半径;④相等的弦所对的圆周角相等;⑤三角形的内心是三角平分线交点;⑥三角形外心到三角形三个顶点距离相等;
A.2个 B.3个 C.4个 D.5个
5.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A. 2 B.3 C.4 D.6
6.直径为4的圆的内接正三角形的边长为( )
A. B. C. D.2
7.一个圆锥和一个圆柱的底面半径相等,且它们的高都等于它们的底面半径,那么它们的侧面积之比为( )
A. B. C. D.
8.如图,半径OA等于弦AB,过B作⊙O的切线BC,取BC=AB,OC交⊙O于E,AC交⊙O于点D,则和的度数分别为( )
A.15°,15° B.30°,15° C.15°,30° D.30°,30°
9.⊙O的半径r=10cm,圆心到直线a的距离OM=8cm,在直线a上有一点P,且PM=6cm,则点P( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.可能⊙O内也可能在外
10.圆柱形油桶(有盖)的底面直径为0.6m,母线长为1m,则油桶的表面积为( )
A. 1.92π B. 0.78π C. 0.69π D. 0.6π
11.如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上一点,且∠EPF=45°,则图中阴影部分面积为( )
A.4-π B.4-2π C.8+π D.8-2π
12.如图,的半径为2,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,则的最大值为( )
A.3 B.14 C.6 D.8
二.填空题(共18分)
13.一个圆柱形容器的底面直径为2dm,要把一块圆心角为240°的扇形铁板做一个圆锥形的盖子,做成的盖子要能盖住圆柱形容器顶部,这个圆锥底面半径至少要有 dm.
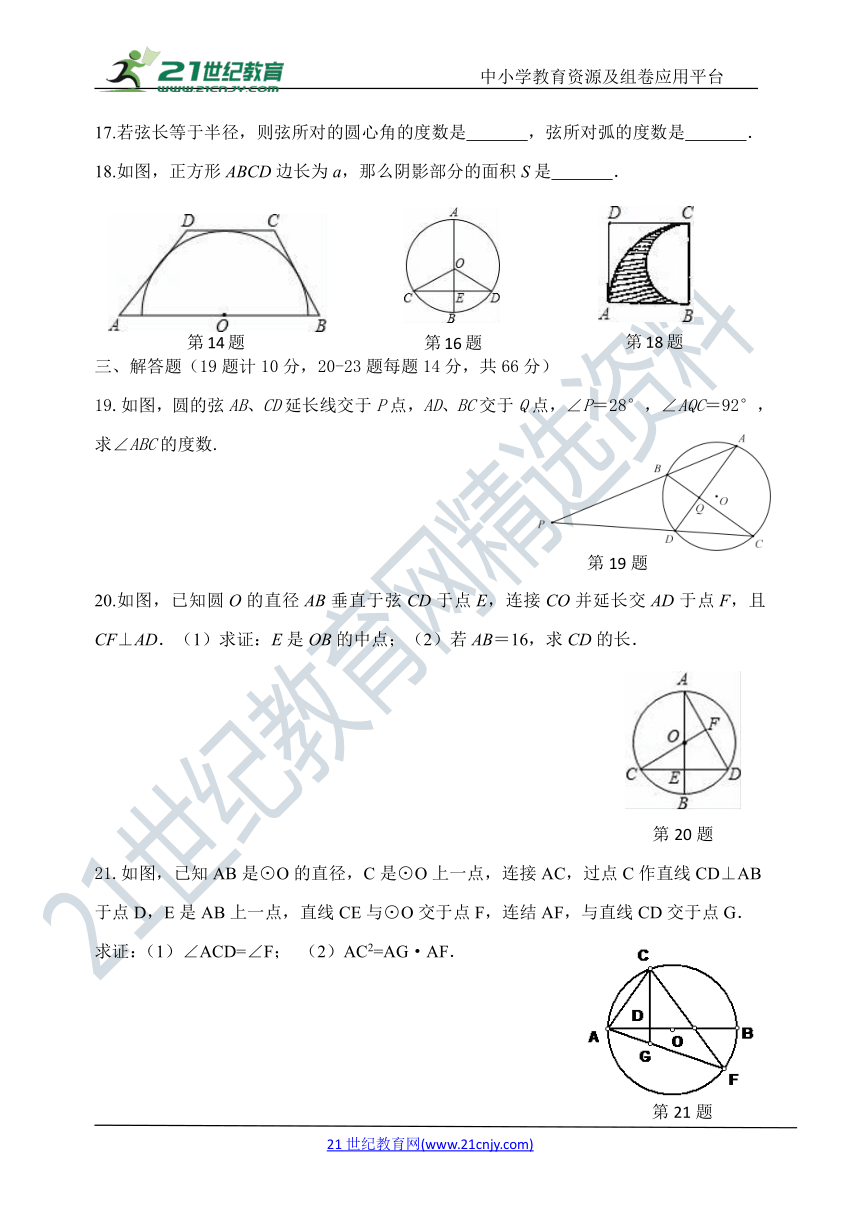
14.如图所示,半圆0的圆心在梯形ABCD的下底AB上,梯形的三边AD,DC,CB均与半圆0相切,已知AD=a,BC=b,则AB的长为 .
15.已知△ABC外切⊙O于D、E、F,这三个点把圆周分成9:5:10三条弧,那么△ABC最大内角为 .
16.已知如图,⊙O中直径AB交CD于E,点B是弧CD的中点,CD=8cm,AE=8cm,则⊙O的半径为 .
17.若弦长等于半径,则弦所对的圆心角的度数是 ,弦所对弧的度数是 .
18.如图,正方形ABCD边长为a,那么阴影部分的面积S是 .
三、解答题(19题计10分,20-23题每题14分,共66分)
19.如图,圆的弦AB、CD延长线交于P点,AD、BC交于Q点,∠P=28°,∠AQC=92°,求∠ABC的度数.
20.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.(1)求证:E是OB的中点;(2)若AB=16,求CD的长.
21.如图,已知AB是⊙O的直径,C是⊙O上一点,连接AC,过点C作直线CD⊥AB于点D,E是AB上一点,直线CE与⊙O交于点F,连结AF,与直线CD交于点G.
求证:(1)∠ACD=∠F; (2)AC2=AG·AF.
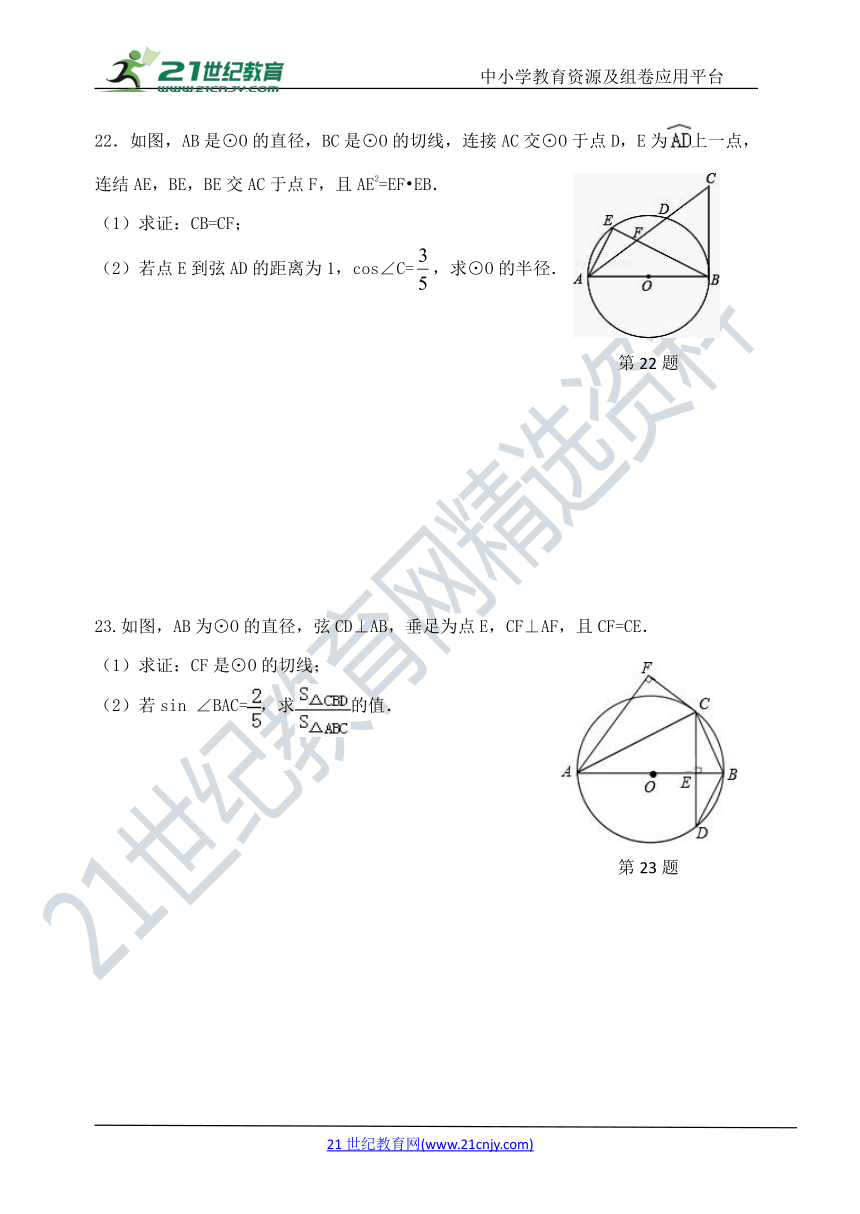
22.如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为上一点,连结AE,BE,BE交AC于点F,且AE2=EF EB.
(1)求证:CB=CF;
(2)若点E到弦AD的距离为1,cos∠C=,求⊙O的半径.
23.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin ∠BAC=,求的值.
第五章《圆》单元测试题B
参考答案与试题解析
一.选择题
A.C.A.A.A.C.D.B.B.B . A.C
二.填空题
13. . 14. a+b.
15.解:∵D、E、F这三个点把圆周分成9:5:10三条弧,
∴∠DOF=75°,∠DOE=135°,∠EOF=150°,
∴由切线的性质得,∠A=105°,∠B=45°,∠C=30°,
∴△ABC最大内角为∠A=105°,
故答案为105°.
16.5.
17.解:∵弦长等于半径,
∴由弦和经过弦的端点的两半径组成等边三角形,
∴弦所对的圆心角的度数是60°;
∴弦所对弧的度数是60°或300°.
故答案为60°;60°或300°.
18.解:根据题意得,S阴影部分=S扇形BAC﹣S半圆BC,
∵S扇形BAC==,
S半圆BC=π(a)2=,
∴S阴影部分=﹣=.
故答案为.
三.解答题
19.60°
20.(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
=,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=16,
∴OC=AB=8,
又∵BE=OE,
∴OE=4,
∴CE===4,
∴CD=2CE=8.
21.①连BC,证∠B=∠ACD=∠F;②证△ACG∽△AFC
22.(1)证明:如图,
∵AE2=EF EB,∴ 。
又∠AEF=∠AEB,∴△AEF∽△AEB。
∴∠1=∠EAB。
∵BC是⊙O的切线,∴∠3=∠EAB。
又∵∠1=∠2,
∴∠2=∠3。∴CB=CF。
(2)如图,连接OE交AC于点G,设⊙O的半径是r,
由(1)知,△AEF∽△AEB,则∠EAF=∠EBA,∴ 。∴OE⊥AD。
∵点E到弦AD的距离为1,∴EG=1。
∵ ,且∠C+∠GAO=90°,∴ 。
∴ ,即 。
解得,r= ,即⊙O的半径是
23. (1)证明:连接OC.
( https: / / gss0. / 7Po3dSag_xI4khGko9WTAnF6hhy / zhidao / pic / item / caef76094b36acafa118474d7fd98d1000e99c83.jpg" \o "点击查看大图 )
∵CE⊥AB,CF ( https: / / www. / s wd=CF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )⊥AF,CE=CF ( https: / / www. / s wd=CF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),
∴AC平分∠BAF ( https: / / www. / s wd=BAF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),即∠BAF ( https: / / www. / s wd=BAF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=2∠BAC ( https: / / www. / s wd=BAC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )。
∵∠BOC ( https: / / www. / s wd=BOC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=2∠BAC ( https: / / www. / s wd=BAC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),∴∠BOC ( https: / / www. / s wd=BOC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=∠BAF ( https: / / www. / s wd=BAF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )。
∴OC∥AF。∴CF ( https: / / www. / s wd=CF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )⊥OC。∴CF是⊙O的切线。
(2)解:∵AB是⊙O的直径,CD ( https: / / www. / s wd=CD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )⊥AB,
∴CE=ED ( https: / / www. / s wd=ED&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),∠ACB=∠BEC ( https: / / www. / s wd=BEC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=90°。
∴S △CBD ( https: / / www. / s wd=CBD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ) =2S △CEB ( https: / / www. / s wd=CEB&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ) ,∠BAC ( https: / / www. / s wd=BAC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=∠BCE。∴△ABC ( https: / / www. / s wd=ABC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )∽△CBE。
∴ ( https: / / gss0. / 9fo3dSag_xI4khGko9WTAnF6hhy / zhidao / pic / item / adaf2edda3cc7cd91fd5e5683a01213fb90e9183.jpg" \o "点击查看大图 ) 。∴ ( https: / / gss0. / 9fo3dSag_xI4khGko9WTAnF6hhy / zhidao / pic / item / d8f9d72a6059252dbef5ccb5379b033b5ab5b9a5.jpg" \o "点击查看大图 )
第12题
第11题
第8题
第5题
第14题
第16题
第18题
第19题
第20题
第21题
第14题
第22题
第23题
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第五章《圆》单元测试题A
时间90分钟,满分120分
一.选择题(共36分)
1.以已知点O为圆心,已知线段a为半径作圆,可以作( )
A.1个 B.2个 C.3个 D.无数个
2.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A. B. C. D.
3.四边形ABCD内接于⊙O,BC是⊙O的直径,若∠ADC=120°,则∠ACB等于( )
A.30° B.40° C.60° D.80°
4.下列命题是真命题的个数是( )
①直径所对的角是90°;②三点确定一个圆;③圆的切线垂直于过切线的半径;④相等的弦所对的圆周角相等;⑤三角形的内心是三角平分线交点;⑥三角形外心到三角形三个顶点距离相等;
A.2个 B.3个 C.4个 D.5个
5.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A. 2 B.3 C.4 D.6
6.直径为4的圆的内接正三角形的边长为( )
A. B. C. D.2
7.一个圆锥和一个圆柱的底面半径相等,且它们的高都等于它们的底面半径,那么它们的侧面积之比为( )
A. B. C. D.
8.如图,半径OA等于弦AB,过B作⊙O的切线BC,取BC=AB,OC交⊙O于E,AC交⊙O于点D,则和的度数分别为( )
A.15°,15° B.30°,15° C.15°,30° D.30°,30°
9.⊙O的半径r=10cm,圆心到直线a的距离OM=8cm,在直线a上有一点P,且PM=6cm,则点P( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.可能⊙O内也可能在外
10.圆柱形油桶(有盖)的底面直径为0.6m,母线长为1m,则油桶的表面积为( )
A. 1.92π B. 0.78π C. 0.69π D. 0.6π
11.如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上一点,且∠EPF=45°,则图中阴影部分面积为( )
A.4-π B.4-2π C.8+π D.8-2π
12.如图,的半径为2,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,则的最大值为( )
A.3 B.14 C.6 D.8
二.填空题(共18分)
13.一个圆柱形容器的底面直径为2dm,要把一块圆心角为240°的扇形铁板做一个圆锥形的盖子,做成的盖子要能盖住圆柱形容器顶部,这个圆锥底面半径至少要有 dm.
14.如图所示,半圆0的圆心在梯形ABCD的下底AB上,梯形的三边AD,DC,CB均与半圆0相切,已知AD=a,BC=b,则AB的长为 .
15.已知△ABC外切⊙O于D、E、F,这三个点把圆周分成9:5:10三条弧,那么△ABC最大内角为 .
16.已知如图,⊙O中直径AB交CD于E,点B是弧CD的中点,CD=8cm,AE=8cm,则⊙O的半径为 .
17.若弦长等于半径,则弦所对的圆心角的度数是 ,弦所对弧的度数是 .
18.如图,正方形ABCD边长为a,那么阴影部分的面积S是 .
三、解答题(19题计10分,20-23题每题14分,共66分)
19.如图,圆的弦AB、CD延长线交于P点,AD、BC交于Q点,∠P=28°,∠AQC=92°,求∠ABC的度数.
20.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.(1)求证:E是OB的中点;(2)若AB=16,求CD的长.
21.如图,已知AB是⊙O的直径,C是⊙O上一点,连接AC,过点C作直线CD⊥AB于点D,E是AB上一点,直线CE与⊙O交于点F,连结AF,与直线CD交于点G.
求证:(1)∠ACD=∠F; (2)AC2=AG·AF.
22.如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为上一点,连结AE,BE,BE交AC于点F,且AE2=EF EB.
(1)求证:CB=CF;
(2)若点E到弦AD的距离为1,cos∠C=,求⊙O的半径.
23.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin ∠BAC=,求的值.
第五章《圆》单元测试题B
参考答案与试题解析
一.选择题
A.C.A.A.A.C.D.B.B.B . A.C
二.填空题
13. . 14. a+b.
15.解:∵D、E、F这三个点把圆周分成9:5:10三条弧,
∴∠DOF=75°,∠DOE=135°,∠EOF=150°,
∴由切线的性质得,∠A=105°,∠B=45°,∠C=30°,
∴△ABC最大内角为∠A=105°,
故答案为105°.
16.5.
17.解:∵弦长等于半径,
∴由弦和经过弦的端点的两半径组成等边三角形,
∴弦所对的圆心角的度数是60°;
∴弦所对弧的度数是60°或300°.
故答案为60°;60°或300°.
18.解:根据题意得,S阴影部分=S扇形BAC﹣S半圆BC,
∵S扇形BAC==,
S半圆BC=π(a)2=,
∴S阴影部分=﹣=.
故答案为.
三.解答题
19.60°
20.(1)证明:连接AC,如图
∵直径AB垂直于弦CD于点E,
=,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=16,
∴OC=AB=8,
又∵BE=OE,
∴OE=4,
∴CE===4,
∴CD=2CE=8.
21.①连BC,证∠B=∠ACD=∠F;②证△ACG∽△AFC
22.(1)证明:如图,
∵AE2=EF EB,∴ 。
又∠AEF=∠AEB,∴△AEF∽△AEB。
∴∠1=∠EAB。
∵BC是⊙O的切线,∴∠3=∠EAB。
又∵∠1=∠2,
∴∠2=∠3。∴CB=CF。
(2)如图,连接OE交AC于点G,设⊙O的半径是r,
由(1)知,△AEF∽△AEB,则∠EAF=∠EBA,∴ 。∴OE⊥AD。
∵点E到弦AD的距离为1,∴EG=1。
∵ ,且∠C+∠GAO=90°,∴ 。
∴ ,即 。
解得,r= ,即⊙O的半径是
23. (1)证明:连接OC.
( https: / / gss0. / 7Po3dSag_xI4khGko9WTAnF6hhy / zhidao / pic / item / caef76094b36acafa118474d7fd98d1000e99c83.jpg" \o "点击查看大图 )
∵CE⊥AB,CF ( https: / / www. / s wd=CF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )⊥AF,CE=CF ( https: / / www. / s wd=CF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),
∴AC平分∠BAF ( https: / / www. / s wd=BAF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),即∠BAF ( https: / / www. / s wd=BAF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=2∠BAC ( https: / / www. / s wd=BAC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )。
∵∠BOC ( https: / / www. / s wd=BOC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=2∠BAC ( https: / / www. / s wd=BAC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),∴∠BOC ( https: / / www. / s wd=BOC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=∠BAF ( https: / / www. / s wd=BAF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )。
∴OC∥AF。∴CF ( https: / / www. / s wd=CF&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )⊥OC。∴CF是⊙O的切线。
(2)解:∵AB是⊙O的直径,CD ( https: / / www. / s wd=CD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )⊥AB,
∴CE=ED ( https: / / www. / s wd=ED&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ),∠ACB=∠BEC ( https: / / www. / s wd=BEC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=90°。
∴S △CBD ( https: / / www. / s wd=CBD&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ) =2S △CEB ( https: / / www. / s wd=CEB&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank ) ,∠BAC ( https: / / www. / s wd=BAC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )=∠BCE。∴△ABC ( https: / / www. / s wd=ABC&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao" \t "https: / / zhidao. / question / _blank )∽△CBE。
∴ ( https: / / gss0. / 9fo3dSag_xI4khGko9WTAnF6hhy / zhidao / pic / item / adaf2edda3cc7cd91fd5e5683a01213fb90e9183.jpg" \o "点击查看大图 ) 。∴ ( https: / / gss0. / 9fo3dSag_xI4khGko9WTAnF6hhy / zhidao / pic / item / d8f9d72a6059252dbef5ccb5379b033b5ab5b9a5.jpg" \o "点击查看大图 )
第12题
第11题
第8题
第5题
第14题
第16题
第18题
第19题
第20题
第21题
第14题
第22题
第23题
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
