第13章 平面图形的认识复习课件

课件56张PPT。§13 平面图形的认识复 习 课复习巩固三角形、多边形、圆、以及尺规作图的知识，构建知识网络图；理解并熟记重点知识；理解难点知识
会用上述知识进行简单的计算、推理和作图.
学习整理知识的方法，学习与人交流
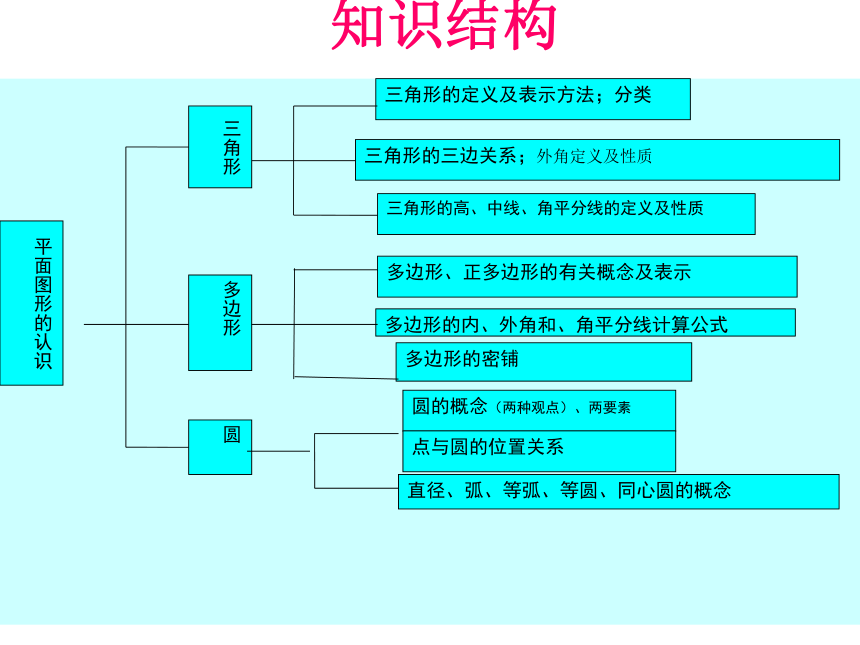
复习目标知识结构三角形的定义及表示方法；分类三角形的高、中线、角平分线的定义及性质多边形、正多边形的有关概念及表示多边形的内、外角和、角平分线计算公式多边形的密铺圆的概念（两种观点）、两要素直径、弧、等弧、等圆、同心圆的概念三角形多边形圆平面图形的认识三角形的三边关系；外角定义及性质
点与圆的位置关系三角形知识
1.三角形的概念
由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。组成三角形的线段叫做三角形的边；相邻两边的公共端点叫做三角形的顶点；相邻两边所组成的角叫做三角形的内角，简称三角形的角。
2.
三角形有下面三个特性：
（1）三角形有三条线段
（2）三条线段不在同一直线上 三角形是封闭图形
（3）首尾顺次相接
三角形用符号“”表示，顶点是A、B、C的三角形记作“ABC”，读作“三角形ABC”。
3.三角形中的主要线段及数量关系
（1）三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线。
（2）在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线。
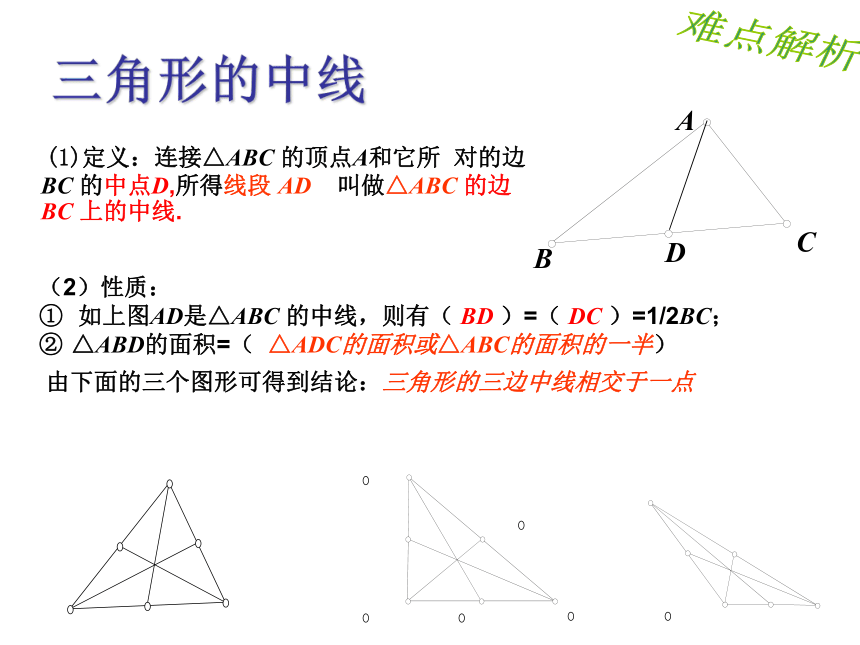
（3）从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）。三角形的中线 (1)定义：连接△ABC 的顶点A和它所 对的边 BC 的中点D,所得线段 AD 叫做△ABC 的边BC 上的中线.
（2）性质：
如上图AD是△ABC 的中线，则有（ BD ）=（ DC ）=1/2BC；
△ABD的面积=（ △ADC的面积或△ABC的面积的一半） 由下面的三个图形可得到结论：三角形的三边中线相交于一点
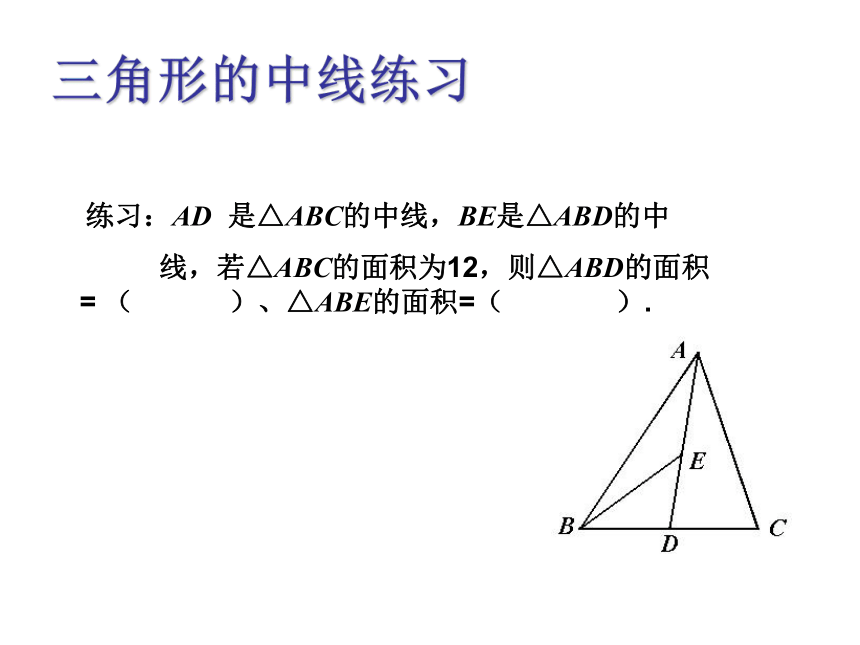
难点解析三角形的中线练习 练习：AD 是△ABC的中线，BE是△ABD的中
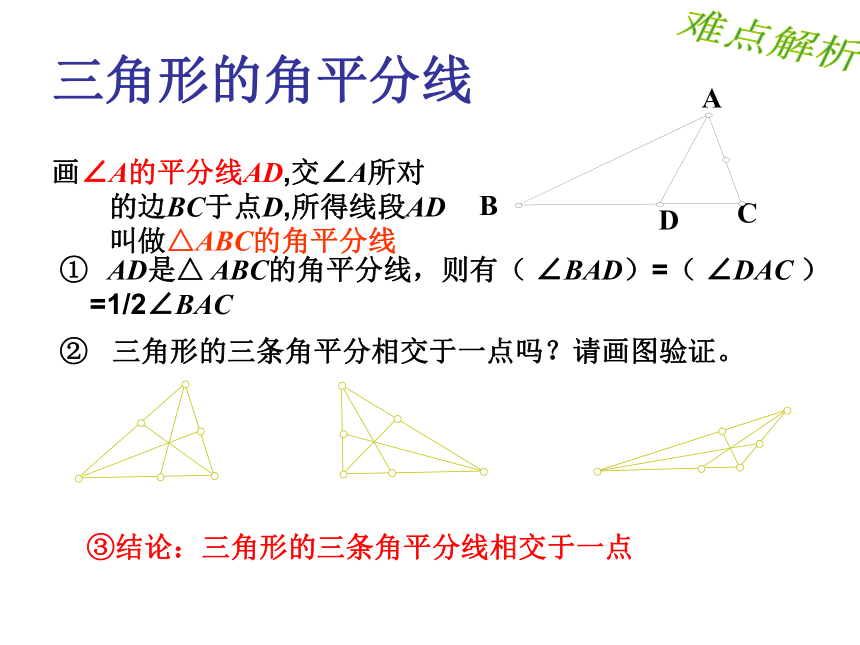
线，若△ABC的面积为12，则△ABD的面积= （ ）、△ABE的面积=（ ）.三角形的角平分线画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做△ABC的角平分线
AD是△ ABC的角平分线，则有（ ∠BAD）=（ ∠DAC ）=1/2∠BAC
② 三角形的三条角平分相交于一点吗？请画图验证。
③结论：三角形的三条角平分线相交于一点
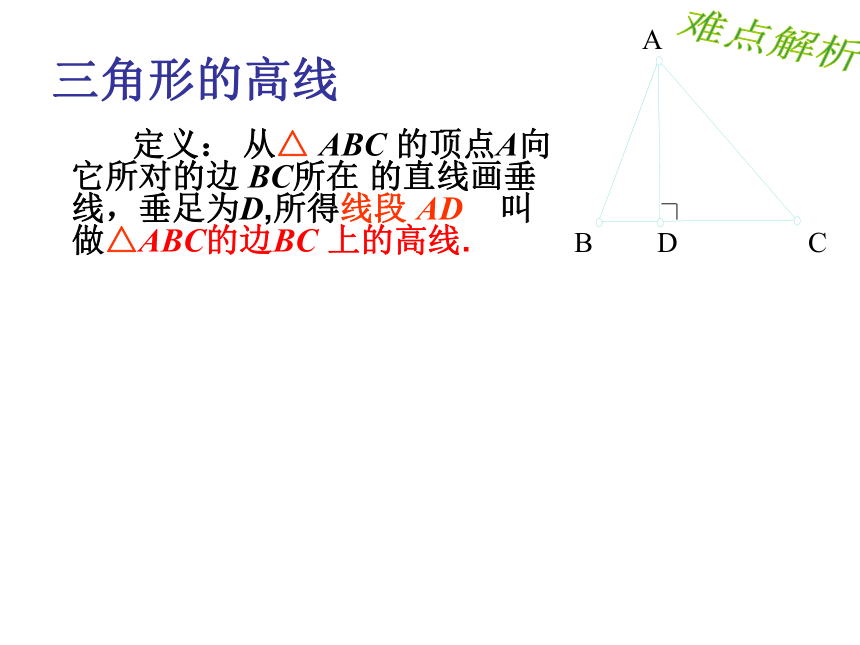
难点解析三角形的高线 定义： 从△ ABC 的顶点A向它所对的边 BC所在 的直线画垂线，垂足为D,所得线段 AD 叫做△ABC的边BC 上的高线.
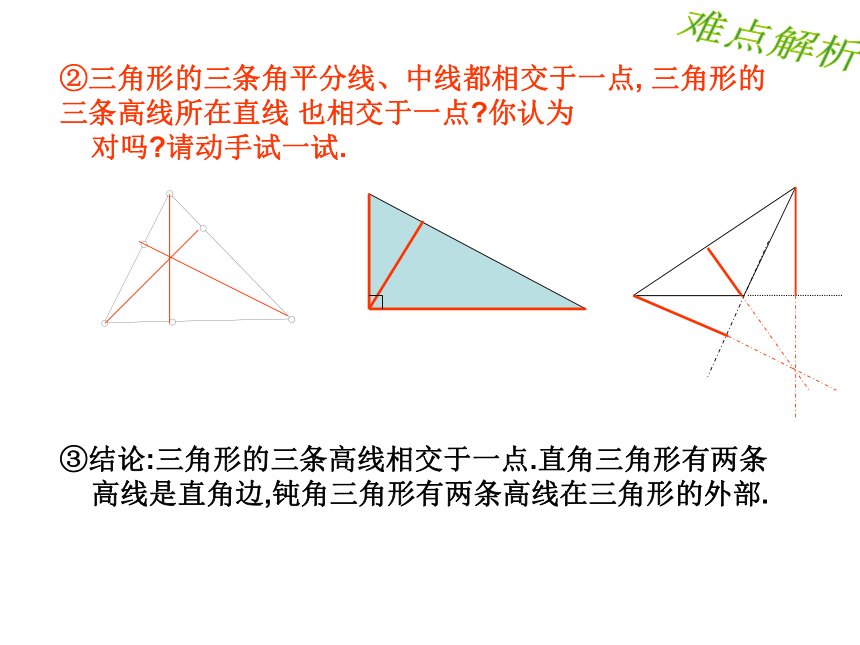
难点解析②三角形的三条角平分线、中线都相交于一点, 三角形的三条高线所在直线 也相交于一点?你认为 对吗?请动手试一试.③结论:三角形的三条高线相交于一点.直角三角形有两条
高线是直角边,钝角三角形有两条高线在三角形的外部.
难点解析三角形知识
5.三角形的三边关系定理及推论
（1）三角形三边关系定理：三角形的两边之和大于第三边。
（2）三角形三边关系定理及推论的作用：
判断三条已知线段能否组成三角形
6.三角形的内角和定理及推论
三角形的内角和定理：三角形三个内角和等于180°。
推论：
①直角三角形的两个锐角互余。
②三角形的一个外角等于和它不相邻的来两个内角的和。
③三角形的一个外角大于任何一个和它不相邻的内角。
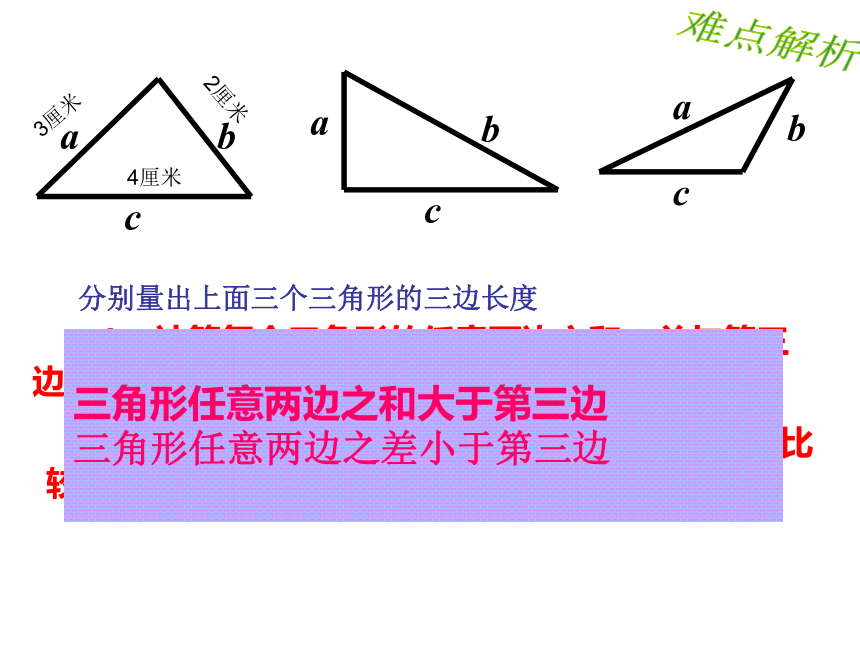
7.三角形的面积 三角形的面积= ×底×高　　分别量出上面三个三角形的三边长度　2.计算每个三角形的任意两边之差，并与第三边比较，你能得到什么结论？　　1、计算每个三角形的任意两边之和，并与第三边比较，你能得到什么结论？
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
2厘米3厘米4厘米难点解析·新课标　三角形内角与外角的应用80° ·新课标 如图，已知BF为△ABC的角平分线，CD为△ABC的外角∠ACE的平分线，它与BF的延长线交于D，请说明∠A=2∠D的理由。ADCEBF21多边形知识
1.多边形的定义
在平面内，由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
2.多边形的表示、边、角、外角
3.多边形的对角线
4多边形的内角和
5多边形的外角和
6、正多边形
问题：1.多边形对角线条数计算公式是 。公式中n-3的含义是什么？
2.多边形内角和公式中n-2的含义是什么？
3.多边形内角和是如何推导出的？
00122539414n-3难点解析………………3456nn-2(n－2) ·180°(n－2) ·180°1 ×180°n-3难点解析总结：n边形内角和公式n边形内角和=(n－2) ·180°难点解析多边形内角和探究方法1　　从多边形的一个顶点出发，把一个多边形分成几个三角形.难点解析E
ABCDO探究2180°× 5 – 360°= 540°180°× 5=900°？五边形内角和540°？？难点解析把一个五边形分成几个三角形，还有其他的分法吗？ABCDEF180° × 4 – 180° = 540°探究3难点解析探究4 A BCDE4 × 180°-180 °O=540°难点解析密铺
1、密铺的定义
2、密铺的条件
3、密铺举例（1）同一种正多边形能密铺地面的只有三种:正三角形、
正方形、正六边形．
（3）用一种形状、大小完全相同的三角形，四边形也能密铺地面．
（2）圆的初步知识
1.圆的定义
（1）（运动的观点）: 在一个平面内,一条线段绕它的一个端点旋转一周,另一个端随之旋转所形成的的封闭图形叫做圆。固定的端点叫做圆心,线段叫做半径
（2）（集合的观点）圆是到定点的距离等于定长的点的集合
2.圆的表示：
3.点与圆的三种位置关系：
（1）点在圆上（2）点在圆内（3）点在圆外
4. （1）圆的内部是 点的集合.
（2）圆的外部是 点的集合.
5.弦、直径；弧的定义、表示及弧的分类；扇形；等圆，同心圆，等弧
6.圆的周长、面积；圆环、半圆、四分之一圆的面积的计算
7.集合观点、参数思想1.图中以BC为边的三角形有 ，∠BED是
的内角， 的外角.
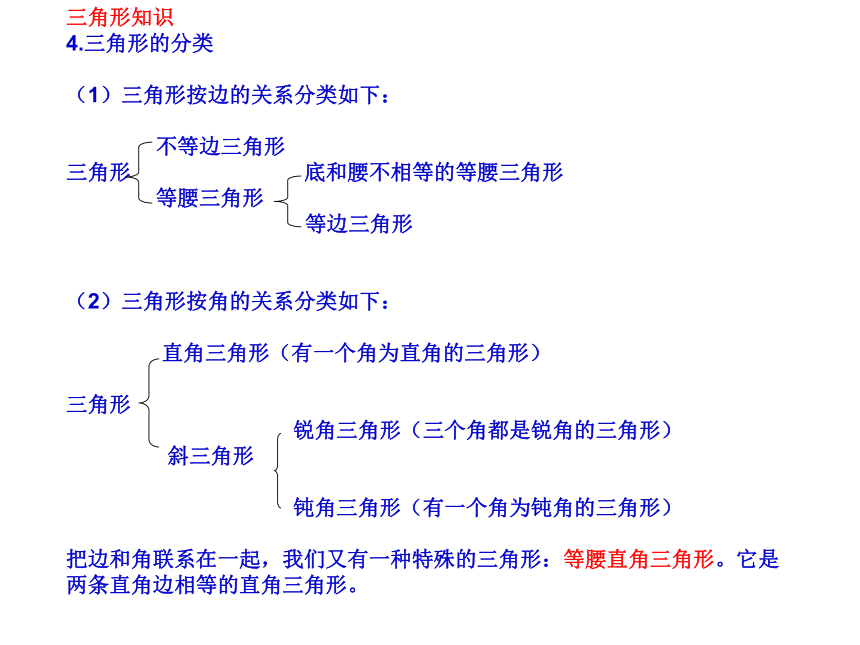
2.三角形的分类
（1）三角形按边分可分为 三角形和 三角形
（2）三角形按角分可分为 三角形、 三角形
和 三角形
3.分别画出图中的高、角平分线、中线
环节一 基础知识复习4.等腰三角形的两边分别是4和6，则周长为 .
5.多边形的内角和为 ，外角和为 ，对角线条数为 .
6.点与圆的位置关系有三种，分别是 ， ， .
如何判断？
基础是关键环节二 专题讲解题组一 三角形的三边关系
三角形的三边为a、b、c，用不等式表示三边关
系为: 利用这一性质可以解决如何构造三
角形的问题和求三角形边长的取值范围.跟踪练习1.有5条线段，长分别为1、2、3、4、5，以其中的三条为边，可以组成 个三角形，它们的边长分别为 .看谁掌握得好题组二：三角形的角平分线例2.如图，△ABC中，BO、CO是角平分线.
若 ∠A=60°，则∠BOC= ，
若∠A=90°，则∠BOC= ，
若∠A=120°，则∠BOC= ，
猜想∠BOC和∠A之间的关系，并证明.合理猜想 大胆尝试反馈练习1.求图中∠A+∠B+∠C+∠D+∠E的度数.2.如图∠B=45°,∠A=30°,
∠C=25°,求∠ADC的大小.题组四：多边形的性质 利用多边形的性质可以解决求边数和角的度数的问题.
例4.（1）若一个多边形的边数增加1，则这个多 边形的内角和增加 度.
（2）若将n边形的边数增加一倍，则它的内角和增加 度.
（3）已知多边形的边数恰好是从一个顶点出发的对角线数的2倍，求此多边形的边数与内角和.实战演练1.已知八边形的每个内角相等，求每个内角的度数。
2.已知正n边形的每个内角与其外角的差为90°，求边数n.看看谁的运算速度快达标检测1.已知等腰三角形的两边长为5和10，则第三边长为 ，周长为 .
2.有两根长为8cm、5cm的木棒，木工师傅要制作一个三角形，如果第三根木棒的长为整数，则第三根木棒的长度有哪几种选法？
3.如图，在直角△ABC中，∠C=90°，
AD平分∠BAC，BE平分∠ABC，
则∠APB= 度.
4.求图中∠A+∠B+∠C+∠D+∠E的度数.5.一个凸多边形的每一个内角都等于140°，那么从这个多边形的一个顶点出发地对角线的条数是（ ）
A.9 B.8 C.7 D.6
6.已知⊙ O的周长为10.
（1）若PO=5.5，则点P与圆的位置关系是什么?
（2）若PO=4，则点P与圆的位置关系是什么?
（3）若PO= ,则点P在圆上.细心决定成败1、在△ABC中，
（1）若∠A＝400，∠B－∠C＝400，
则∠B ＝＿＿∠C＝＿＿＿
（2）、若∠A＝　 ∠B＝　∠C，

则∠A＝＿＿＿∠B＝＿＿＿∠C＝＿＿＿900500300600900课堂练习
2、如图，在△ABC中，∠A、∠B的平
分线相交于点I，若∠C＝700，则∠AIB
＝＿＿，若∠AIB＝1550，则∠C＝＿＿＿。
3、如图，∠1＋∠2＋∠3＋∠4＋∠5=320o
∠6＝＿＿＿＿
12501300400
5、已知：三角形的3边长分别为1，x，5，
且x为整数，则x＝＿＿＿＿＿。56、如图，∠O的两边被一直线所截，用α和β的式子
表示∠O的度数为（　　）
A、α－β　　　　　B、β－α
C、1800－α＋β　　D、1800－α－β
7、在△ABC中，如果∠A＋∠B＝2∠C，∠A≠∠B，那么（　　）
A、∠A、∠B、∠C都不等于600　
B、∠A＝600 C、∠B＝600，　　
D、∠C＝600BD9、若一个多边形的内角和是外角和的3.5倍，则此多边形的边数是（　　）
A、7　　B、14　　　C、9　　　D、18
10、直角三角形两锐角的平分线所交成的角的度数是（　　）
A、45o　　　B、135o　　　C、45o或135o　　D、以上答案都不对CB11、如图，在△ABC中，∠BAC＝4∠ABC＝4∠C，BD⊥AC，垂足为D，求∠ABD的度数。解：设∠C＝x，则，∠ABC＝x,∠BAC=4x根据三角形内角和性质：
x+x+4x=1800,x=300即：∠BAC＝1200，所以∠BAD＝600又因为：BD⊥AC，即∠D＝900所以：∠ABD＝3001.如果两条直线被第三条直线所截,那么下面的结论:①同位角相等;②内错角相等;③同旁内角互补;④一定有内错角.其中正确的结论有 （ ）
A.1个 B.2个 C.3个 D.4个2.如图,∠a的同旁内角有 ( )
A.1个 B.2个
C.3个 D.4个a3.如图，有下列四个判断:
①因为∠4=∠6，所以∠2=∠5；②因为∠4=∠6，所以∠3=∠5；③因为∠5+∠7=180°，所以∠4=∠6；④因为∠4=∠6 ，所以∠1+∠7=180°.其中正确的判断有 （ ）
A.1个 B.2个
C.3个 D.4个
1527364cabd1.图中的内错角有______对.2.如图,已知AB//CD, ∠a=125 °, ∠1=∠2,则∠B=_________.ABCDE12a3.如图,已知∠1=90°+a, ∠2= 90°- a(0°A、一条射线平分三角形的一个内角，那么这条射线是三角形的角平分线。
B、垂直于三角形一边的直线是三角形的高。
C、过三角形一边的中点的直线叫三角形的中线。
D、三角形的角平分线、中线、高都是线段
2、已知等腰三角形的两边长分别是4CM与9CM，则第三边长为_________。
3、四边形的内角和是________，内角和为1800°的多边形是________边形。
AD是△ABC的高，BE平分∠ABC交AD于E，若∠C=70°，∠BED=64°，求∠ BAC的度数。
ABCDE 在△ABC中，AB=9，BC=2，若AC的长为偶数，那么△ABC的周长是多少？ 如图,AD是∠CAE的平分线, ∠B=25°,∠DAE=50 °,求∠ ACD的度数.BACDE105°　　如图，求∠Ａ＋∠Ｂ＋∠Ｃ＋∠Ｄ＋∠Ｅ＋∠Ｆ的度数．ＡＢＣＤＥＦＮＭＯ　 把一张长方形纸条如图那样折叠后，测得∠ＣＧＯ＝５０ ° ，则∠ＧＯＢ＇为多少度？ＡＣＯＢＤＧＢ＇Ｄ＇　　一个多边形的每个内角都是１５０°，求这个多边形的内角和． 若多边行的每个内角都相等,且每个内角都是其外角的4倍,求这个多边形的边数.1.已知在△ABC中, ∠A=∠B+∠C,则∠A=__________.
2.若n边形的内角和是外角和的3倍,则n=___________.
3.在△ABC中,AD是角平分线, ∠B=70°, ∠C=40 °,则∠DAC= __________.
4.已知等腰三角形的周长为20,其中一边长是4,则另外两边长分别为_________.
5.如图,点B、C、D在一条直线上,则∠1, ∠2, ∠ B的大小关系是___________.CBAD216.已知在四边形ABCD中,∠A+∠C=∠B+ ∠D, ∠A的外角为120°,求∠C的度数.8、如图把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，∠A与∠1＋∠2之间的数量关系保持不变，请找一找这个规律，你发现的规律是 （　　　）
A、∠A＝∠1＋∠2　 B、2∠A＝∠1＋∠2
C、3∠A＝2∠1＋∠2 D、3∠A＝2（∠1＋∠2）B