青岛版【2014年新版】八年级数学下册课件:6.4三角形中位线定理(28页)(共28张PPT)
文档属性
| 名称 | 青岛版【2014年新版】八年级数学下册课件:6.4三角形中位线定理(28页)(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-14 06:44:24 | ||
图片预览



文档简介
课件28张PPT。 三角形的中位线6.4三角形的中位线定理
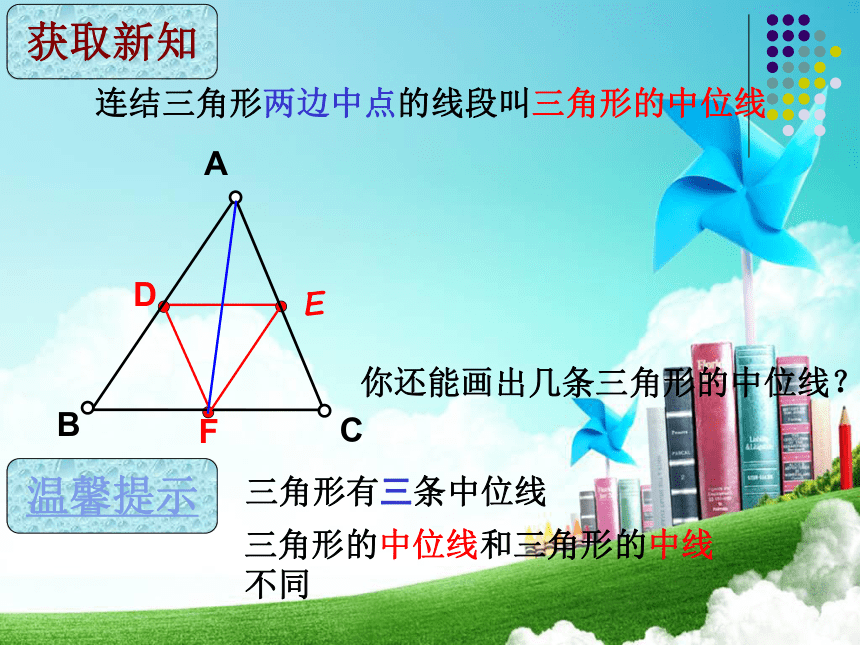
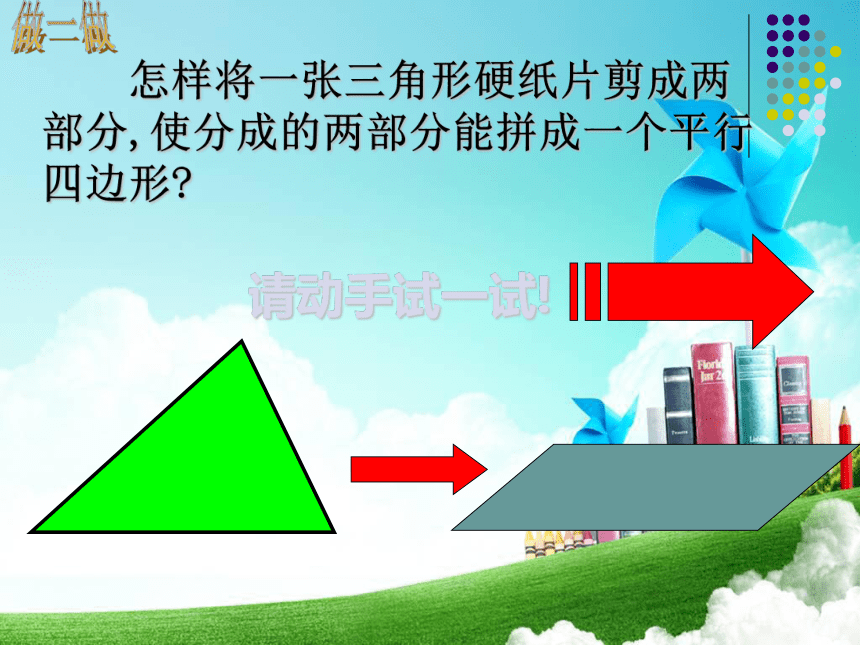
如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。创设情境,导入新课温馨提示连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线三角形的中位线和三角形的中线不同EDF获取新知你还能画出几条三角形的中位线? (1)相同之处——都和边的中点有关;
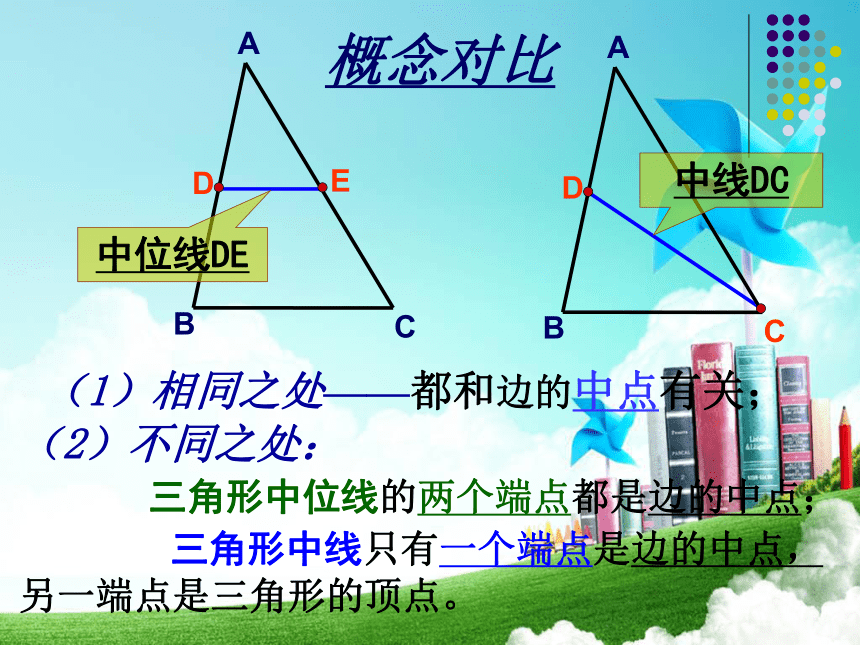
(2)不同之处:
三角形中位线的两个端点都是边的中点;
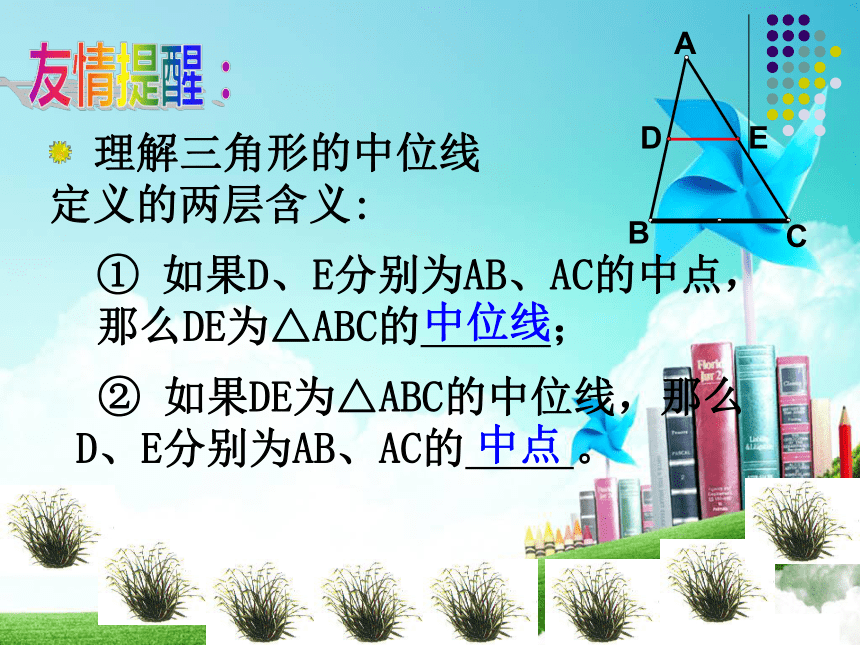
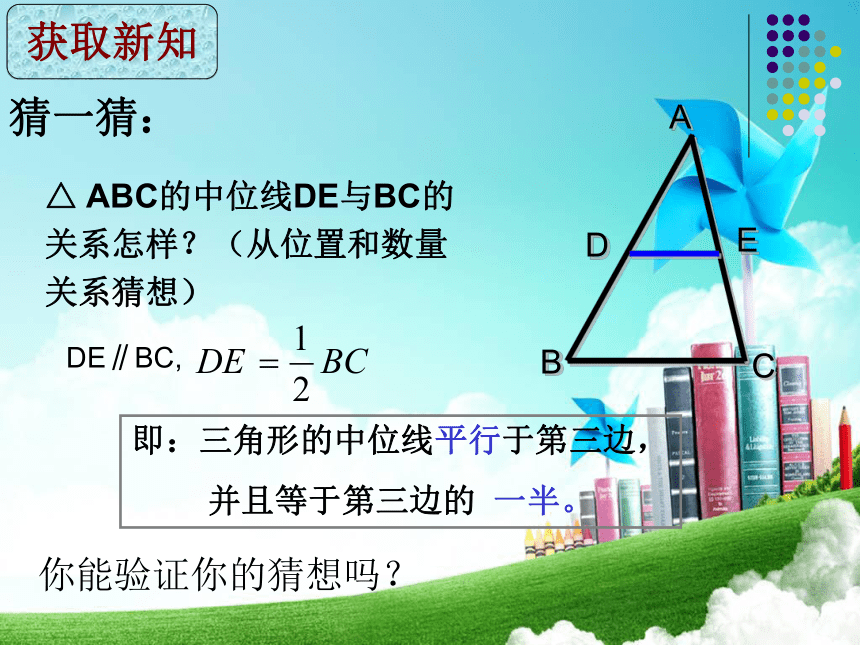
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。概念对比中线DC中位线DE友情提醒: 理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;CBAED中位线中点猜一猜:△ ABC的中位线DE与BC的关系怎样?(从位置和数量关系猜想)获取新知DE∥BC,即:三角形的中位线平行于第三边,
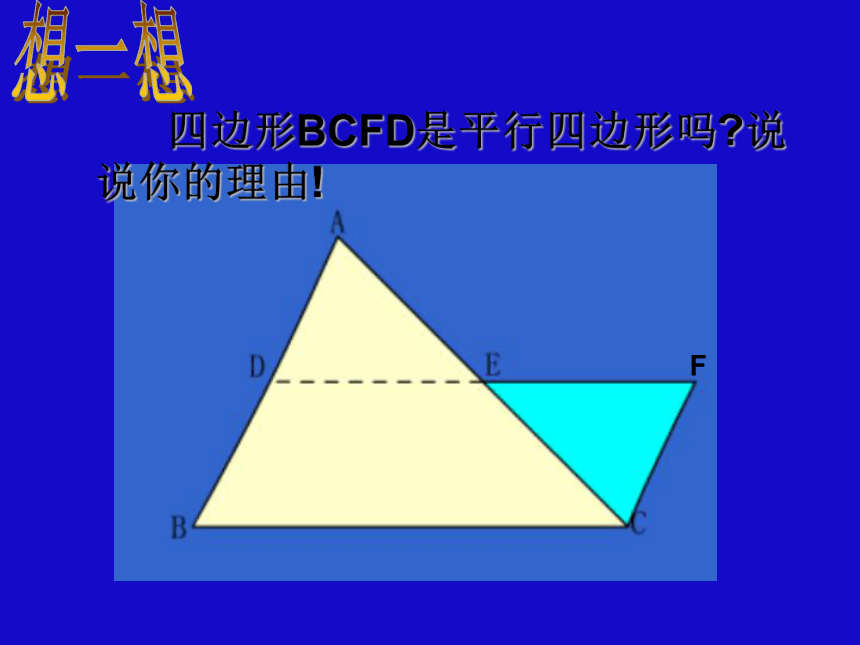
并且等于第三边的 一半。你能验证你的猜想吗?做一做 四边形BCFD是平行四边形吗?说说你的理由!想一想证一证分析:
延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CFE,
得CF=AE , ∠A=∠ACF
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
三角形中位线定理 三角形的中位线平行且等于第三边的一半.几何语言:∵DE是△ABC的中位线① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半用 途如图所示,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时, 那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减少
C.线段EF的长不变 D.线段EF的长不能确定
C初试身手初试身手EDF初试身手若∠ADE=65°,则∠B= 度,为什么?若BC=8cm,则DE= cm,为什么?654若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点9cm若△ABC的周长为24,△DEF的周长是_____121、 三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系?探究活动2、三角形三条中位线围成的三角形的面积与原三角形的面积有什么关系?图中有_____个平行四边形若△ABC的面积为24,△DEF的面积是_____36设 计 方 案: F
(中点)(中点)DE(中点)ABC A、B两点被池塘隔开,如何才能知道它们之间的距离呢? 在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?说一说CBA2040在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 。ABDCEFGH11大展身手 已知: 在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.
求证∠PMN=∠PNM.大展身手E,F是AB,BC的中点,你联想到什么? 要使EF成为一个三角形的中位线应怎样添加辅助线? 证明:如图,连接AC∵EF是△ABC的中位线同理得: ∴四边形EFGH是平行四边形典例示范 答: 四边形EFGH为平行四边形。拓展 (1)顺次连结对角线相等的四边形各边中点所得的四边形是什么?(3)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么? (2)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?菱形矩形正方形ABCDABCDFEGH结 论互相垂直矩形相等菱形互相垂直且相等正方形既不互相垂直也不相等平行四边形 实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关. (1)?顺次连结平行四边形各边中点所得的四边形是什么?(2)顺次连结菱形各边中点所得的四边形是什么?平行四边形矩形 (3)顺次连结正方形各边中点所得的四边形是什么? 正方形(4)顺次连结矩形各边中点所得的四边形是什么?例2已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点. 求证(1)四边形EFGH是平行四边形。
(2)请增加一个条件使得四边形ADFE为菱形。
(3) 请增加一个条件使得四边形ADFE为矩形。(4)能不能只增加一个条件使得四边形ADFE为正方形。
例1 求证三角形的一条中位线与第三边上的中线互相平分.已知: 如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.C例: 求证三角形的一条中位线与第三边上的中线互相平分.已知: 如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例3:已知 ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点。求 证:∠HEF= ∠FGH。说一说你学到了什么?作业:
1.P32练习第1题,习题第2题(书上)
2.完成练习册及资料上相对应的题。
如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。创设情境,导入新课温馨提示连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线三角形的中位线和三角形的中线不同EDF获取新知你还能画出几条三角形的中位线? (1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。概念对比中线DC中位线DE友情提醒: 理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;CBAED中位线中点猜一猜:△ ABC的中位线DE与BC的关系怎样?(从位置和数量关系猜想)获取新知DE∥BC,即:三角形的中位线平行于第三边,
并且等于第三边的 一半。你能验证你的猜想吗?做一做 四边形BCFD是平行四边形吗?说说你的理由!想一想证一证分析:
延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CFE,
得CF=AE , ∠A=∠ACF
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
三角形中位线定理 三角形的中位线平行且等于第三边的一半.几何语言:∵DE是△ABC的中位线① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半用 途如图所示,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时, 那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减少
C.线段EF的长不变 D.线段EF的长不能确定
C初试身手初试身手EDF初试身手若∠ADE=65°,则∠B= 度,为什么?若BC=8cm,则DE= cm,为什么?654若AC=4cm,BC=6cm,AB=8cm,
则△DEF的周长=______.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点9cm若△ABC的周长为24,△DEF的周长是_____121、 三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系?探究活动2、三角形三条中位线围成的三角形的面积与原三角形的面积有什么关系?图中有_____个平行四边形若△ABC的面积为24,△DEF的面积是_____36设 计 方 案: F
(中点)(中点)DE(中点)ABC A、B两点被池塘隔开,如何才能知道它们之间的距离呢? 在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?说一说CBA2040在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 。ABDCEFGH11大展身手 已知: 在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.
求证∠PMN=∠PNM.大展身手E,F是AB,BC的中点,你联想到什么? 要使EF成为一个三角形的中位线应怎样添加辅助线? 证明:如图,连接AC∵EF是△ABC的中位线同理得: ∴四边形EFGH是平行四边形典例示范 答: 四边形EFGH为平行四边形。拓展 (1)顺次连结对角线相等的四边形各边中点所得的四边形是什么?(3)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么? (2)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?菱形矩形正方形ABCDABCDFEGH结 论互相垂直矩形相等菱形互相垂直且相等正方形既不互相垂直也不相等平行四边形 实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关. (1)?顺次连结平行四边形各边中点所得的四边形是什么?(2)顺次连结菱形各边中点所得的四边形是什么?平行四边形矩形 (3)顺次连结正方形各边中点所得的四边形是什么? 正方形(4)顺次连结矩形各边中点所得的四边形是什么?例2已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点. 求证(1)四边形EFGH是平行四边形。
(2)请增加一个条件使得四边形ADFE为菱形。
(3) 请增加一个条件使得四边形ADFE为矩形。(4)能不能只增加一个条件使得四边形ADFE为正方形。
例1 求证三角形的一条中位线与第三边上的中线互相平分.已知: 如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.C例: 求证三角形的一条中位线与第三边上的中线互相平分.已知: 如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例3:已知 ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点。求 证:∠HEF= ∠FGH。说一说你学到了什么?作业:
1.P32练习第1题,习题第2题(书上)
2.完成练习册及资料上相对应的题。
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
