青岛版【2014年新版】八年级数学下册课件:8.1不等式的基本性质(23页)(共23张PPT)
文档属性
| 名称 | 青岛版【2014年新版】八年级数学下册课件:8.1不等式的基本性质(23页)(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-14 00:00:00 | ||
图片预览








文档简介
课件23张PPT。8.1不等式的基本性质温故知新1、观察下面两组式子:
第一组:1+2=3; a+b=b+a; S = ab; 4+x = 7.
第二组:-7 < -5; 3+4 > 1+4; 2x ≤6,
a+2 ≥0; 3≠4.
第一组都是 ,第二组是 2、像-7 < -5; 3+4 > 1+4; 2x ≤6,a+2 ≥0; 3≠4等表示不等关系的式子叫做不等式判断下列式子是不是不等式:(1)-3<0; (2)4x+3y>0
(3)x=3; (4) X2+xy+y2
(5)x≠5; (6)X+2>y+5;
等式基本性质1:等式的两边都加上(或减去)同一个整式,所得结果仍是等式等式基本性质2:等式的两边都乘以(或除以)同一个不为0的数,所得结果仍是等式如果a=b,那么a±c=b±c如果a=b,那么ac=bc,a÷c=b÷c(c≠0)观察:用“<”或“>”填空,并找一找其中的规律.(2) –1<3 -1+2____3+2
-1-3____3-36>4 6+2____4+2
6-2____4-2>><<发现:当不等式两边加上或减去同一个数时,不等号的方向________不变探索与发现如果a>b,那么a+c b+c, a-c b-c.如果a<b,那么a+c b+c, a-c b-c;>><<不等式的基本性质1不等式两边都加(或减去)
同一个数,不等号的方向不变.不等式两边都加上(或减去)
同一个整式,不等号的方向不变.(1)∵0 1,
∴ a a+1( )
(2)∵a2 0,
∴a2-2 -2( )
(3)若x+1>0,两边同加上-1,得_______
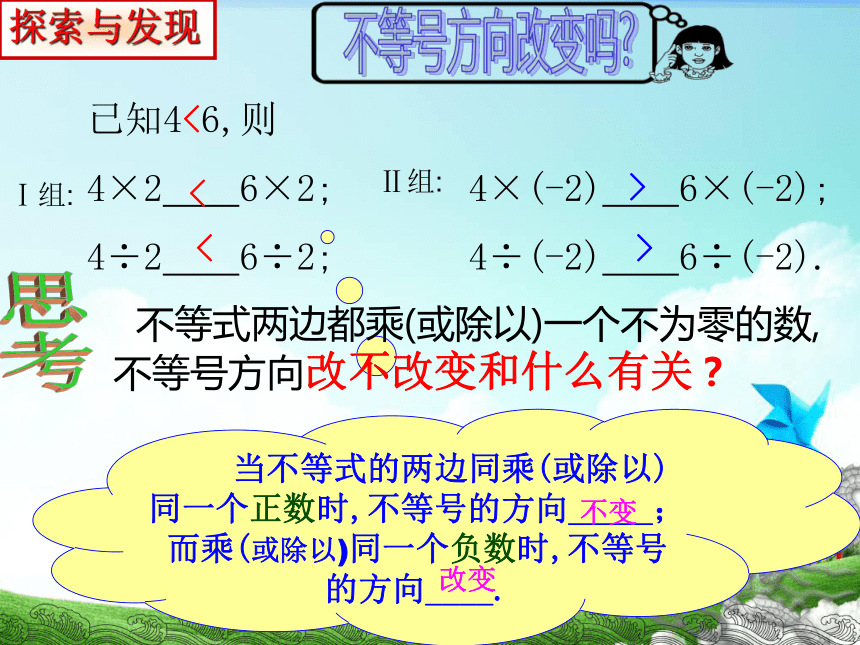
(依据:_____________________).选择适当的不等号填空:<≥≥x >-1不等式的基本性质1小试牛刀对了!对了!不等式的基本性质1不等式的基本性质1< 当不等式的两边同乘(或除以)同一个正数时,不等号的方向_____;而乘(或除以)同一个负数时,不等号的方向____.已知4<6,则
4×2 6×2; 4×(-2) 6×(-2);
4÷2 6÷2; 4÷(-2) 6÷(-2). <<>> 不等式两边都乘(或除以)一个不为零的数,不等号方向改不改变和什么有关?思考探索与发现不等号方向改变吗?Ⅰ组:Ⅱ组:不变改变不等式的两边都乘(或都除以)同一个正数,不等号的方向不变
不等式的两边都乘以(或都除以)同一个负数,必须把不等号的方向改变.如果a>b,且c>0,那么ac>bc,
如果a>b,且c<0,那么ac<bc,不等式的基本性质2、3不等式性质1:
不等式两边同时加上( 或减去 )同一个整式,不等号的方向不变。
不等式性质2:
不等式两边同时乘以( 或除以 )同一个正数,不等号的方向不变。
不等式性质3:
不等式两边乘( 或除以 )同一个负数,不等号的方向改变。
(2)-2<-1,两边都加上-a,得 ;(1)若x+1>0,两边都减去1,得 ;x+1>0-1-1-1>x>-1-2-a<-1-ax>练一练(4)∵0<1, ∴a a+1;+4+4<(5)若a>-b,则a+b 0.(3)若a-4>0,则a 4;>>>先前后比较再定不等号练一练(6)若m>-3,则-3m 9;(8)若-a<b,则a -b.(7)若a≥b,则2a 2b; ×(-3) ×(-3)><≥>先前后比较再定不等号练一练设m>n,用“>”或“<”填空。 (1) m-5____ n-5
(2) m+4 ____ n+4
(3) 6m ____ 6n
(4) -3m ____ -3n试一试,看谁更快2.已知m(a-3)n,求a的范围. 1.已知x>y,比较2-3x与2-3y的大小.先×(-3),再+2先×(-3),再+2×(a-3)×(a-3)<>试一试先前后比较再定不等号解: 由题意可得:a-3<0(不等式的基本性质3)
∴a<3(不等式的基本性质2)例1:已知x>y,试比较-2x和-2y的大小,并说明理由
变式4:若x>y,比较(a-3)x与(a-3)y的大小?崭露头角例2:由 >2可得( )2 >2 ,不等式两边同时乘了 ,
你能由 >2,推出 <2.5吗?崭露头角(1)若k<0,则下列不等式中不成立的是( )
A.k+2>k-2 B.-6k>0
C.k>-k D.k<-k
(2)已知a A.4a<4b B.-4a<-4b
C.a+4n,且amA.a>0 B.a<0 C.a=0 D.a0
2、若k<0,则下列不等式中不成立的是( )
A.k+2>k-2 B.-6k>0 C.k>-k D.k<-k
3、用“<”或“>”填空:
(1)a a+1 (2)a+2 a-2 (3)1-a -a (4)a2 0(a≠0)拓展延伸感悟与反思 通过这节课的学习活动你有哪些收获?等式与不等式的基本性质等式两边都加上(或减去)同一个整式,所得结果仍是等式不等式两边都加(或减去)同一个整式,不等号方向不变.等式两边都乘(或除以)同一个不为零的数,所得结果仍是等式.比较归纳不等式两边都乘(或除以)同一个正数,不等号方向不变;不等式两边都乘(或除以)同一个负数,不等号方向改变.作业1、习题8.1第4、5、6、7题;
2、选作:习题8.1第8题。
再见
第一组:1+2=3; a+b=b+a; S = ab; 4+x = 7.
第二组:-7 < -5; 3+4 > 1+4; 2x ≤6,
a+2 ≥0; 3≠4.
第一组都是 ,第二组是 2、像-7 < -5; 3+4 > 1+4; 2x ≤6,a+2 ≥0; 3≠4等表示不等关系的式子叫做不等式判断下列式子是不是不等式:(1)-3<0; (2)4x+3y>0
(3)x=3; (4) X2+xy+y2
(5)x≠5; (6)X+2>y+5;
等式基本性质1:等式的两边都加上(或减去)同一个整式,所得结果仍是等式等式基本性质2:等式的两边都乘以(或除以)同一个不为0的数,所得结果仍是等式如果a=b,那么a±c=b±c如果a=b,那么ac=bc,a÷c=b÷c(c≠0)观察:用“<”或“>”填空,并找一找其中的规律.(2) –1<3 -1+2____3+2
-1-3____3-36>4 6+2____4+2
6-2____4-2>><<发现:当不等式两边加上或减去同一个数时,不等号的方向________不变探索与发现如果a>b,那么a+c b+c, a-c b-c.如果a<b,那么a+c b+c, a-c b-c;>><<不等式的基本性质1不等式两边都加(或减去)
同一个数,不等号的方向不变.不等式两边都加上(或减去)
同一个整式,不等号的方向不变.(1)∵0 1,
∴ a a+1( )
(2)∵a2 0,
∴a2-2 -2( )
(3)若x+1>0,两边同加上-1,得_______
(依据:_____________________).选择适当的不等号填空:<≥≥x >-1不等式的基本性质1小试牛刀对了!对了!不等式的基本性质1不等式的基本性质1< 当不等式的两边同乘(或除以)同一个正数时,不等号的方向_____;而乘(或除以)同一个负数时,不等号的方向____.已知4<6,则
4×2 6×2; 4×(-2) 6×(-2);
4÷2 6÷2; 4÷(-2) 6÷(-2). <<>> 不等式两边都乘(或除以)一个不为零的数,不等号方向改不改变和什么有关?思考探索与发现不等号方向改变吗?Ⅰ组:Ⅱ组:不变改变不等式的两边都乘(或都除以)同一个正数,不等号的方向不变
不等式的两边都乘以(或都除以)同一个负数,必须把不等号的方向改变.如果a>b,且c>0,那么ac>bc,
如果a>b,且c<0,那么ac<bc,不等式的基本性质2、3不等式性质1:
不等式两边同时加上( 或减去 )同一个整式,不等号的方向不变。
不等式性质2:
不等式两边同时乘以( 或除以 )同一个正数,不等号的方向不变。
不等式性质3:
不等式两边乘( 或除以 )同一个负数,不等号的方向改变。
(2)-2<-1,两边都加上-a,得 ;(1)若x+1>0,两边都减去1,得 ;x+1>0-1-1-1>x>-1-2-a<-1-ax>练一练(4)∵0<1, ∴a a+1;+4+4<(5)若a>-b,则a+b 0.(3)若a-4>0,则a 4;>>>先前后比较再定不等号练一练(6)若m>-3,则-3m 9;(8)若-a<b,则a -b.(7)若a≥b,则2a 2b; ×(-3) ×(-3)><≥>先前后比较再定不等号练一练设m>n,用“>”或“<”填空。 (1) m-5____ n-5
(2) m+4 ____ n+4
(3) 6m ____ 6n
(4) -3m ____ -3n试一试,看谁更快2.已知m
∴a<3(不等式的基本性质2)例1:已知x>y,试比较-2x和-2y的大小,并说明理由
变式4:若x>y,比较(a-3)x与(a-3)y的大小?崭露头角例2:由 >2可得( )2 >2 ,不等式两边同时乘了 ,
你能由 >2,推出 <2.5吗?崭露头角(1)若k<0,则下列不等式中不成立的是( )
A.k+2>k-2 B.-6k>0
C.k>-k D.k<-k
(2)已知a
C.a+4
2、若k<0,则下列不等式中不成立的是( )
A.k+2>k-2 B.-6k>0 C.k>-k D.k<-k
3、用“<”或“>”填空:
(1)a a+1 (2)a+2 a-2 (3)1-a -a (4)a2 0(a≠0)拓展延伸感悟与反思 通过这节课的学习活动你有哪些收获?等式与不等式的基本性质等式两边都加上(或减去)同一个整式,所得结果仍是等式不等式两边都加(或减去)同一个整式,不等号方向不变.等式两边都乘(或除以)同一个不为零的数,所得结果仍是等式.比较归纳不等式两边都乘(或除以)同一个正数,不等号方向不变;不等式两边都乘(或除以)同一个负数,不等号方向改变.作业1、习题8.1第4、5、6、7题;
2、选作:习题8.1第8题。
再见
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
