北师大版八年级数学上册 第五章二元一次方程组单元测试 含解析
文档属性
| 名称 | 北师大版八年级数学上册 第五章二元一次方程组单元测试 含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 909.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 09:15:27 | ||
图片预览



文档简介
北师大版八上二元一次方程组单元测试
(共23题,共100分)
一、选择题(共10题,共30分)
(3分)下列各组数中,是二元一次方程 的一个解的是
A. B. C. D.
(3分)用加减法解方程组 下列解法错误的是
A.① ② ,消去
B.① ② ,消去
C.① ② ,消去
D.① ② ,消去
(3分)篮球联赛中每场比赛都要分岀胜负,毎队胜 场得 分,负 场得 分,某队在 场比赛中得到 分,那么这个队负的场数是
A. 场 B. 场 C. 场 D. 场
(3分)小亮的妈妈用 元钱买了甲、乙两种水果,甲种水果每千克 元,乙种水果每千克 元,且乙种水果比甲种水果少买了 千克,求小亮妈妈两种水果各买了多少千克?设小亮妈妈买了甲种水果 千克,乙种水果 千克,则可列方程组为
A. B. C. D.
(3分)如图,用 块相同的矩形墙砖拼成一个矩形,设矩形墙砖的长和宽分别为 厘米和 厘米,依题意列方程组正确的是
A. B.
C. D.
(3分)两个一次函数 与 ,它们在一直角坐标系中的图象可能是
A. B.
C. D.
(3分)已知 , 两地相距 ,上午 时,亮亮从 地步行到 地, 时芳芳从 地出发骑自行车到 地,亮亮和芳芳两人离 地的距离 与亮亮所用时间 之间的函数关系如图所示,芳芳到达 地时间为
A. B. C. D.
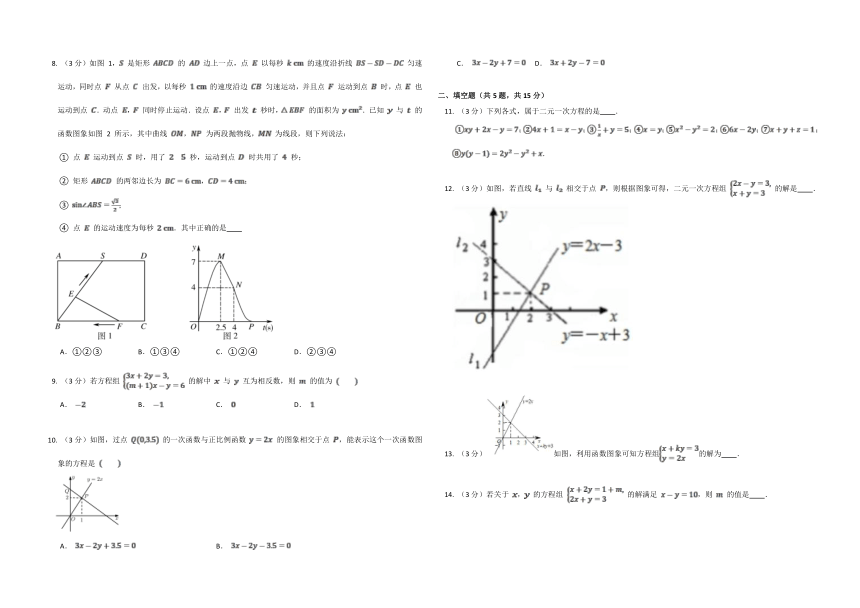
(3分)如图 1, 是矩形 的 边上一点,点 以每秒 的速度沿折线 匀速运动,同时点 从点 出发,以每秒 的速度沿边 匀速运动,并且点 运动到点 时,点 也运动到点 .动点 , 同时停止运动.设点 , 出发 秒时, 的面积为 .已知 与 的函数图象如图 2 所示,其中曲线 , 为两段抛物线, 为线段,则下列说法:
① 点 运动到点 时,用了 秒,运动到点 时共用了 秒;
② 矩形 的两邻边长为 ,;
③ ;
④ 点 的运动速度为每秒 .其中正确的是
A.①②③ B.①③④ C.①②④ D.②③④
(3分)若方程组 的解中 与 互为相反数,则 的值为
A. B. C. D.
(3分)如图,过点 的一次函数与正比例函数 的图象相交于点 ,能表示这个一次函数图象的方程是
A. B.
C. D.
二、填空题(共5题,共15分)
(3分)下列各式,属于二元一次方程的是 .
;;;;;;;.
(3分)如图,若直线 与 相交于点 ,则根据图象可得,二元一次方程组 的解是 .
(3分)如图,利用函数图象可知方程组的解为 .
(3分)若关于 , 的方程组 的解满足 ,则 的值是 .
(3分)一条船顺流速度为 ,逆流速度为 ,若设船在静水中的速度为 ,水流的速度为 ,则可列方程组为 .
三、解答题(共8题,共55分)
(6分)解二元一次方程组
(6分)用代入消元法解下列方程组:
(1)
(2)
(6分)有一批画册,如果 人合看 本,那么余 本;如果 人合看 本,就有 人没得看.共有多少人?多少本画册?
(6分)在某市“棚户区改造”建设工程中,有甲、乙两种车辆参加运土.已知 辆甲种车和 辆乙种车一次共可运土 立方米, 辆甲种车和 辆乙种车一次共可运土 立方米.求甲、乙两种车每辆一次分别可运土多少立方米.
(6分)从甲地到乙地的路有一段上坡与一段平路.如果保持上坡每小时走 ,平路每小时走 ,下坡每小时走 ,那么从甲地到乙地需 分,从乙地到甲地需要 分.甲地到乙地全程是多少?
(8分)如图,直线 与 轴, 轴分别交于点 ,,另一直线 与 , 轴分别交于点 ,,两直线相交于点 .
(1) 求点 的坐标.
(2) 连接 ,求 的面积.
(8分)在平面直角坐标系 中,直线 与反比例函数 的图象的一个交点为 .
(1) 求 的值;
(2) 直线 与 轴交于点 ,与 轴交于点 ,连接 ,设 的面积为 , 的面积为 ,若 ,求 的取值范围.
(9分)为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有A,B两种型号的挖掘机,已知 台A型和 台B型挖掘机同时施工一小时挖土 立方米; 台A型和 台B型挖掘机同时施工一小时挖土 立方米.每台A型挖掘机一小时的施工费用为 元,每台B型挖掘机一小时的施工费用为 元.
(1) 分别求每台A型,B型挖掘机一小时挖土多少立方米?
(2) 若不同数量的A型和B型挖掘机共 台同时施工 小时,至少完成 立方米的挖土量,且总费用不超过 元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
答案
一、选择题(共10题,共30分)
1. 【答案】D
【知识点】探究二元一次方程的解
2. 【答案】A
【解析】A、① ② 得 ,此选项错误;
B、① ② 得:,此选项正确;
C、① ② 得 ,此选项正确;
D、① ② 得:,此选项正确.
故选:A.
【知识点】加减消元
3. 【答案】A
【解析】设这个队胜 场,负 场,
根据题意,得
解得
所以负了 场,故选:A.
【知识点】积分问题
4. 【答案】A
【解析】【解析】 设小亮妈妈买了甲种水果x kg,乙种水果y kg,根据两种水果共花去28元,乙种水果比甲种水果少买了2 kg,据此列方程组\begin{cases}4x+6y=28,\\x=y+2.\end{cases}
【知识点】二元一次方程(组)的应用
5. 【答案】A
【解析】根据图示可得,
矩形的宽可表示为 ,
而矩形的宽又为 厘米,即
矩形的长可表示为 ,又可表示为 ,
即 ,即
联立①②有
故A选项正确.
【知识点】几何问题
6. 【答案】C
【知识点】一次函数与二元一次方程(组)的关系、k,b对一次函数图象及性质的影响
7. 【答案】C
【解析】由题意可知:
设亮亮 与 的函数关系式为:,
把 , 代入 ,
,
,
,
当 时,此时 ,
设芳芳 与 的函数关系式为:,
把 , 和 , 代入 ,
解得:
,
令 代入 ,
,
故芳芳到达 地的时间为 点 分.
【知识点】一次函数的应用、用函数图象表示实际问题中的函数关系
8. 【答案】C
【解析】点 在 上运动时, 与 的关系为曲线 ,点 在 上运动时, 与 的关系为线段 ,点 在 上运动时, 与 的关系为曲线 .
设 ,.
则有 解得
设 的速度为 ,则 ,,.
在 中,根据勾股定理可得,.
所以 .
【知识点】函数关系的表示、二元一次方程(组)的应用
9. 【答案】C
【解析】
且
联立①③得
代入②得 ,
.
【知识点】含参二元一次方程组
10. 【答案】D
【解析】设这个一次函数的解析式为 .
这条直线经过点 和点 ,
解得
故这个一次函数的解析式为 ,即:.
【知识点】一次函数与二元一次方程(组)的关系
二、填空题(共5题,共15分)
11. 【答案】
【知识点】二元一次方程
12. 【答案】
【解析】根据题意知,
二元一次方程组 的解就是直线 与 的交点 的坐标,
又 ,
原方程组的解是:
【知识点】加减消元
13. 【答案】
【解析】【分析】观察函数的图象与相交于点,,从而求解;
【解析】解:观察图象可知,与相交于点,,
可求出方方程组的解为,
故答案为:
【点评】此题主要考查一次函数与二元一次方程组,关键是能根据函数图象的交点解方程组.
【知识点】一次函数与二元一次方程(组)的关系
14. 【答案】
【解析】
② ①,得 ,即 ,
又 ,
,解得 .
【知识点】含参二元一次方程组
15. 【答案】由题意,
得
【知识点】行程问题
三、解答题(共8题,共55分)
16. 【答案】① ②,得把 代入②,得解得 原方程组的解为
【知识点】加减消元
17. 【答案】
(1)
(2)
【知识点】代入消元
18. 【答案】设共有 人, 本画册.
根据题意,得解得答:共有 人, 本画册.
【知识点】综合应用
19. 【答案】设甲种车辆一次运土 立方米,乙车辆一次运土 立方米,由题意得,解得:答:甲种车辆一次运土 立方米,乙车辆一次运土 立方米.
【知识点】二元一次方程(组)的应用
20. 【答案】上坡路程 ,平路 ,
根据题意得:解得 全程总共 .
【知识点】行程问题
21. 【答案】
(1)
.
(2) 连接 ,
,
,,,
,
,
.
【知识点】一次函数与二元一次方程(组)的关系、坐标平面内图形的面积
22. 【答案】
(1) .
(2) 由题意,得 .
①当直线 过点 和 时,解得②当直线 过点 和 时,解得 或 .
【知识点】一次函数的解析式、反比例函数图像上的点的坐标特征
23. 【答案】
(1) 设每台A型,B型挖掘机一小时分别挖土 立方米和 立方米,根据题意,得解得所以,每台A型挖掘机一小时挖土 立方米,每台B型挖掘机一小时挖土 立方米.
(2) 设A型挖掘机有 台,总费用为 元,则B型挖掘机有 台.根据题意,得 ,
因为 解得
又因为 ,解得 ,
所以 .
所以,共有三种调配方案,
方案一;当 时,,即A型挖掘机 台,B型挖掘机 台;
方案二;当 时,,即A型挖掘机 台,B型挖掘机 台;
方案三;当 时,,即A型挖掘机 台,B型挖掘机 台.
因为 ,由一次函数的性质可知, 随 的减小而减小,
所以当 时,,
此时A型挖掘机 台,B型挖掘机 台的施工费用最低,最低费用为 元.
【知识点】二元一次方程组的应用、一次函数的应用
(共23题,共100分)
一、选择题(共10题,共30分)
(3分)下列各组数中,是二元一次方程 的一个解的是
A. B. C. D.
(3分)用加减法解方程组 下列解法错误的是
A.① ② ,消去
B.① ② ,消去
C.① ② ,消去
D.① ② ,消去
(3分)篮球联赛中每场比赛都要分岀胜负,毎队胜 场得 分,负 场得 分,某队在 场比赛中得到 分,那么这个队负的场数是
A. 场 B. 场 C. 场 D. 场
(3分)小亮的妈妈用 元钱买了甲、乙两种水果,甲种水果每千克 元,乙种水果每千克 元,且乙种水果比甲种水果少买了 千克,求小亮妈妈两种水果各买了多少千克?设小亮妈妈买了甲种水果 千克,乙种水果 千克,则可列方程组为
A. B. C. D.
(3分)如图,用 块相同的矩形墙砖拼成一个矩形,设矩形墙砖的长和宽分别为 厘米和 厘米,依题意列方程组正确的是
A. B.
C. D.
(3分)两个一次函数 与 ,它们在一直角坐标系中的图象可能是
A. B.
C. D.
(3分)已知 , 两地相距 ,上午 时,亮亮从 地步行到 地, 时芳芳从 地出发骑自行车到 地,亮亮和芳芳两人离 地的距离 与亮亮所用时间 之间的函数关系如图所示,芳芳到达 地时间为
A. B. C. D.
(3分)如图 1, 是矩形 的 边上一点,点 以每秒 的速度沿折线 匀速运动,同时点 从点 出发,以每秒 的速度沿边 匀速运动,并且点 运动到点 时,点 也运动到点 .动点 , 同时停止运动.设点 , 出发 秒时, 的面积为 .已知 与 的函数图象如图 2 所示,其中曲线 , 为两段抛物线, 为线段,则下列说法:
① 点 运动到点 时,用了 秒,运动到点 时共用了 秒;
② 矩形 的两邻边长为 ,;
③ ;
④ 点 的运动速度为每秒 .其中正确的是
A.①②③ B.①③④ C.①②④ D.②③④
(3分)若方程组 的解中 与 互为相反数,则 的值为
A. B. C. D.
(3分)如图,过点 的一次函数与正比例函数 的图象相交于点 ,能表示这个一次函数图象的方程是
A. B.
C. D.
二、填空题(共5题,共15分)
(3分)下列各式,属于二元一次方程的是 .
;;;;;;;.
(3分)如图,若直线 与 相交于点 ,则根据图象可得,二元一次方程组 的解是 .
(3分)如图,利用函数图象可知方程组的解为 .
(3分)若关于 , 的方程组 的解满足 ,则 的值是 .
(3分)一条船顺流速度为 ,逆流速度为 ,若设船在静水中的速度为 ,水流的速度为 ,则可列方程组为 .
三、解答题(共8题,共55分)
(6分)解二元一次方程组
(6分)用代入消元法解下列方程组:
(1)
(2)
(6分)有一批画册,如果 人合看 本,那么余 本;如果 人合看 本,就有 人没得看.共有多少人?多少本画册?
(6分)在某市“棚户区改造”建设工程中,有甲、乙两种车辆参加运土.已知 辆甲种车和 辆乙种车一次共可运土 立方米, 辆甲种车和 辆乙种车一次共可运土 立方米.求甲、乙两种车每辆一次分别可运土多少立方米.
(6分)从甲地到乙地的路有一段上坡与一段平路.如果保持上坡每小时走 ,平路每小时走 ,下坡每小时走 ,那么从甲地到乙地需 分,从乙地到甲地需要 分.甲地到乙地全程是多少?
(8分)如图,直线 与 轴, 轴分别交于点 ,,另一直线 与 , 轴分别交于点 ,,两直线相交于点 .
(1) 求点 的坐标.
(2) 连接 ,求 的面积.
(8分)在平面直角坐标系 中,直线 与反比例函数 的图象的一个交点为 .
(1) 求 的值;
(2) 直线 与 轴交于点 ,与 轴交于点 ,连接 ,设 的面积为 , 的面积为 ,若 ,求 的取值范围.
(9分)为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有A,B两种型号的挖掘机,已知 台A型和 台B型挖掘机同时施工一小时挖土 立方米; 台A型和 台B型挖掘机同时施工一小时挖土 立方米.每台A型挖掘机一小时的施工费用为 元,每台B型挖掘机一小时的施工费用为 元.
(1) 分别求每台A型,B型挖掘机一小时挖土多少立方米?
(2) 若不同数量的A型和B型挖掘机共 台同时施工 小时,至少完成 立方米的挖土量,且总费用不超过 元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
答案
一、选择题(共10题,共30分)
1. 【答案】D
【知识点】探究二元一次方程的解
2. 【答案】A
【解析】A、① ② 得 ,此选项错误;
B、① ② 得:,此选项正确;
C、① ② 得 ,此选项正确;
D、① ② 得:,此选项正确.
故选:A.
【知识点】加减消元
3. 【答案】A
【解析】设这个队胜 场,负 场,
根据题意,得
解得
所以负了 场,故选:A.
【知识点】积分问题
4. 【答案】A
【解析】【解析】 设小亮妈妈买了甲种水果x kg,乙种水果y kg,根据两种水果共花去28元,乙种水果比甲种水果少买了2 kg,据此列方程组\begin{cases}4x+6y=28,\\x=y+2.\end{cases}
【知识点】二元一次方程(组)的应用
5. 【答案】A
【解析】根据图示可得,
矩形的宽可表示为 ,
而矩形的宽又为 厘米,即
矩形的长可表示为 ,又可表示为 ,
即 ,即
联立①②有
故A选项正确.
【知识点】几何问题
6. 【答案】C
【知识点】一次函数与二元一次方程(组)的关系、k,b对一次函数图象及性质的影响
7. 【答案】C
【解析】由题意可知:
设亮亮 与 的函数关系式为:,
把 , 代入 ,
,
,
,
当 时,此时 ,
设芳芳 与 的函数关系式为:,
把 , 和 , 代入 ,
解得:
,
令 代入 ,
,
故芳芳到达 地的时间为 点 分.
【知识点】一次函数的应用、用函数图象表示实际问题中的函数关系
8. 【答案】C
【解析】点 在 上运动时, 与 的关系为曲线 ,点 在 上运动时, 与 的关系为线段 ,点 在 上运动时, 与 的关系为曲线 .
设 ,.
则有 解得
设 的速度为 ,则 ,,.
在 中,根据勾股定理可得,.
所以 .
【知识点】函数关系的表示、二元一次方程(组)的应用
9. 【答案】C
【解析】
且
联立①③得
代入②得 ,
.
【知识点】含参二元一次方程组
10. 【答案】D
【解析】设这个一次函数的解析式为 .
这条直线经过点 和点 ,
解得
故这个一次函数的解析式为 ,即:.
【知识点】一次函数与二元一次方程(组)的关系
二、填空题(共5题,共15分)
11. 【答案】
【知识点】二元一次方程
12. 【答案】
【解析】根据题意知,
二元一次方程组 的解就是直线 与 的交点 的坐标,
又 ,
原方程组的解是:
【知识点】加减消元
13. 【答案】
【解析】【分析】观察函数的图象与相交于点,,从而求解;
【解析】解:观察图象可知,与相交于点,,
可求出方方程组的解为,
故答案为:
【点评】此题主要考查一次函数与二元一次方程组,关键是能根据函数图象的交点解方程组.
【知识点】一次函数与二元一次方程(组)的关系
14. 【答案】
【解析】
② ①,得 ,即 ,
又 ,
,解得 .
【知识点】含参二元一次方程组
15. 【答案】由题意,
得
【知识点】行程问题
三、解答题(共8题,共55分)
16. 【答案】① ②,得把 代入②,得解得 原方程组的解为
【知识点】加减消元
17. 【答案】
(1)
(2)
【知识点】代入消元
18. 【答案】设共有 人, 本画册.
根据题意,得解得答:共有 人, 本画册.
【知识点】综合应用
19. 【答案】设甲种车辆一次运土 立方米,乙车辆一次运土 立方米,由题意得,解得:答:甲种车辆一次运土 立方米,乙车辆一次运土 立方米.
【知识点】二元一次方程(组)的应用
20. 【答案】上坡路程 ,平路 ,
根据题意得:解得 全程总共 .
【知识点】行程问题
21. 【答案】
(1)
.
(2) 连接 ,
,
,,,
,
,
.
【知识点】一次函数与二元一次方程(组)的关系、坐标平面内图形的面积
22. 【答案】
(1) .
(2) 由题意,得 .
①当直线 过点 和 时,解得②当直线 过点 和 时,解得 或 .
【知识点】一次函数的解析式、反比例函数图像上的点的坐标特征
23. 【答案】
(1) 设每台A型,B型挖掘机一小时分别挖土 立方米和 立方米,根据题意,得解得所以,每台A型挖掘机一小时挖土 立方米,每台B型挖掘机一小时挖土 立方米.
(2) 设A型挖掘机有 台,总费用为 元,则B型挖掘机有 台.根据题意,得 ,
因为 解得
又因为 ,解得 ,
所以 .
所以,共有三种调配方案,
方案一;当 时,,即A型挖掘机 台,B型挖掘机 台;
方案二;当 时,,即A型挖掘机 台,B型挖掘机 台;
方案三;当 时,,即A型挖掘机 台,B型挖掘机 台.
因为 ,由一次函数的性质可知, 随 的减小而减小,
所以当 时,,
此时A型挖掘机 台,B型挖掘机 台的施工费用最低,最低费用为 元.
【知识点】二元一次方程组的应用、一次函数的应用
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
